Visualizations for 2D Categorical and 1D Quantitative Data

Prof Ron Yurko

2024-09-04

Reminders, previously, and today…

• HW1 is due TONIGHT!

• HW2 is posted (due next Wednesday)

• Discussed data visualization principles and the role of infographics

• Visualized 1D categorical data, i.e., make bar charts!

TODAY:

• Pie charts…

• Visualizing 2D categorical data

• Begin 1D quantitative data

So you want to make pie charts…

penguins |> 
  ggplot(aes(fill = species, x = "")) + 
  geom_bar(aes(y = after_stat(count))) +
  coord_polar(theta = "y") +
  theme_void() 

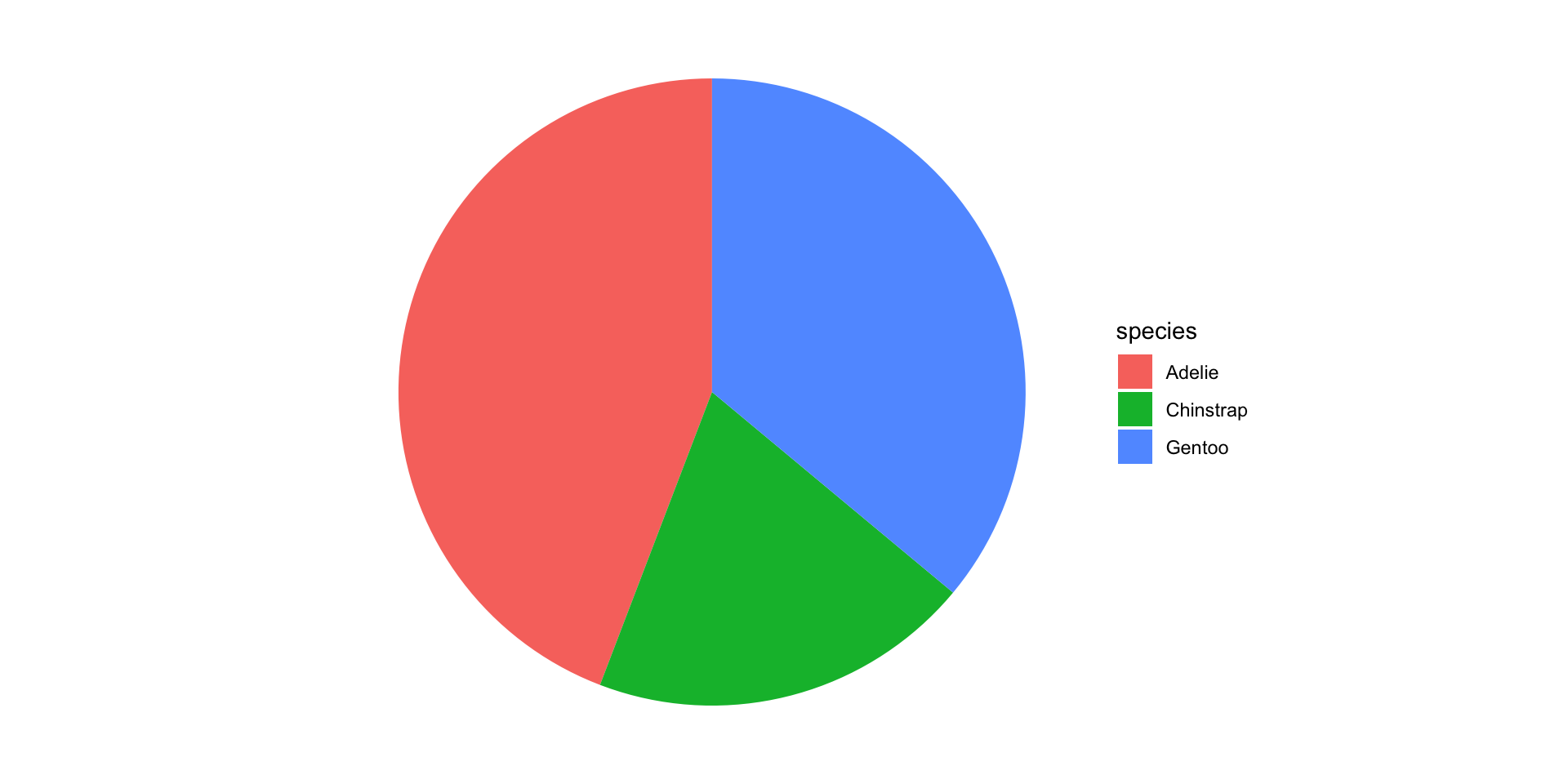
Friends Don’t Let Friends Make Pie Charts

Waffle charts are cooler anyway…

library(waffle)
penguins |>
  group_by(species) |> 
  summarize(count = n(), .groups = "drop") |> 
  ggplot(aes(fill = species, values = count)) +
  geom_waffle(n_rows = 20, color = "white", flip = TRUE) +
  coord_equal() +
  theme_void()

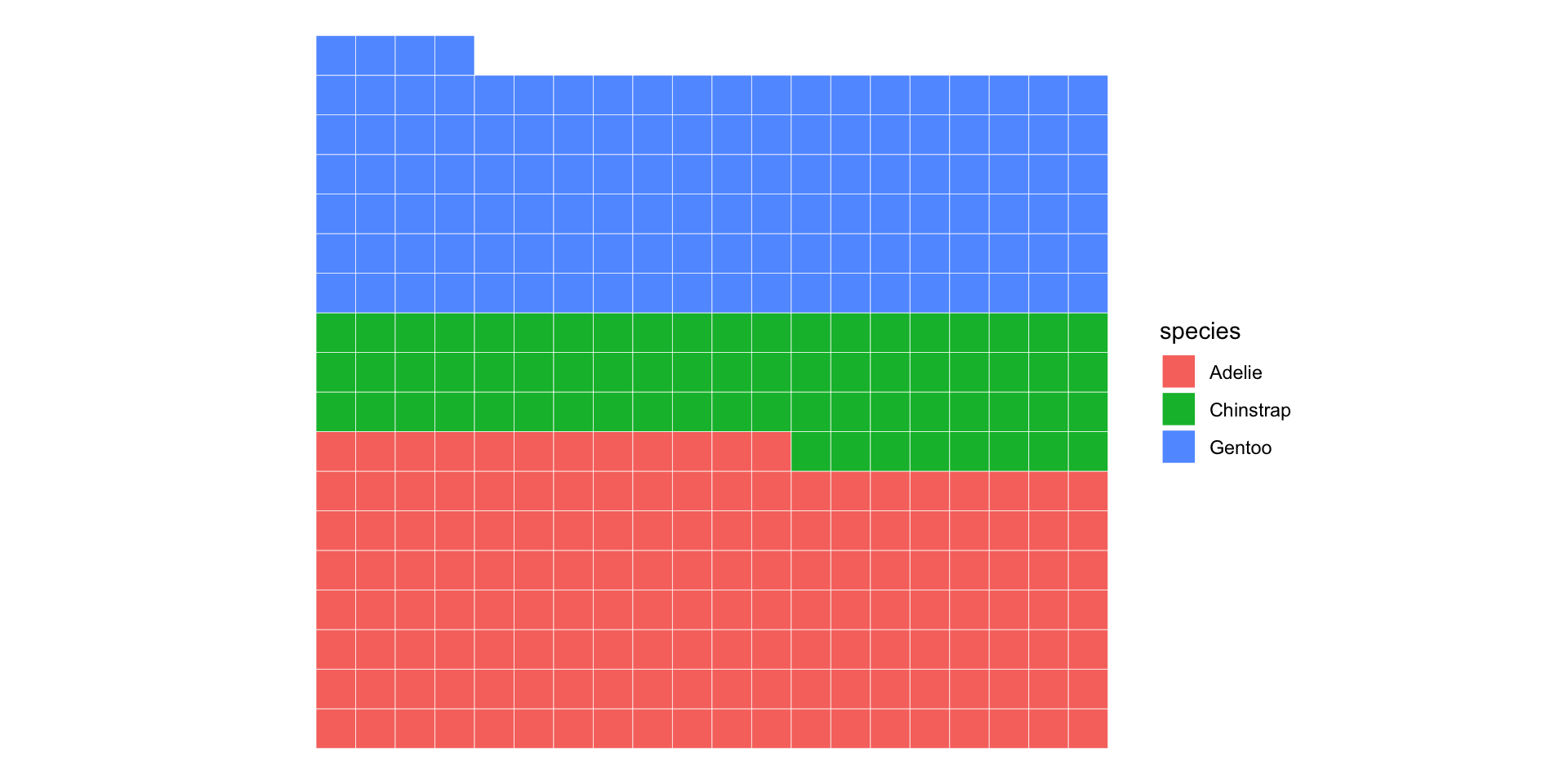
2D categorical basics: marginal / conditional distribution

addmargins(table("Species" = penguins$species, "Island" = penguins$island))

           Island
Species     Biscoe Dream Torgersen Sum
  Adelie        44    56        52 152
  Chinstrap      0    68         0  68
  Gentoo       124     0         0 124
  Sum          168   124        52 344

• Column and row sums: marginal distributions

• Values within rows: conditional distribution for Island given Species

• Values within columns: conditional distribution for Species given Island

• Bottom right: total number of observations

Connecting distributions to visualizations

Five distributions for two categorical variables \(A\) and \(B\):

• Marginals: \(P(A)\) and \(P(B)\)

• Conditionals: \(P(A | B)\) and \(P(B|A)\)

• Joint: \(P(A, B)\)

We use bar charts to visualize marginal distributions for categorical variables…

And we’ll use more bar charts to visualize conditional and joint distributions!

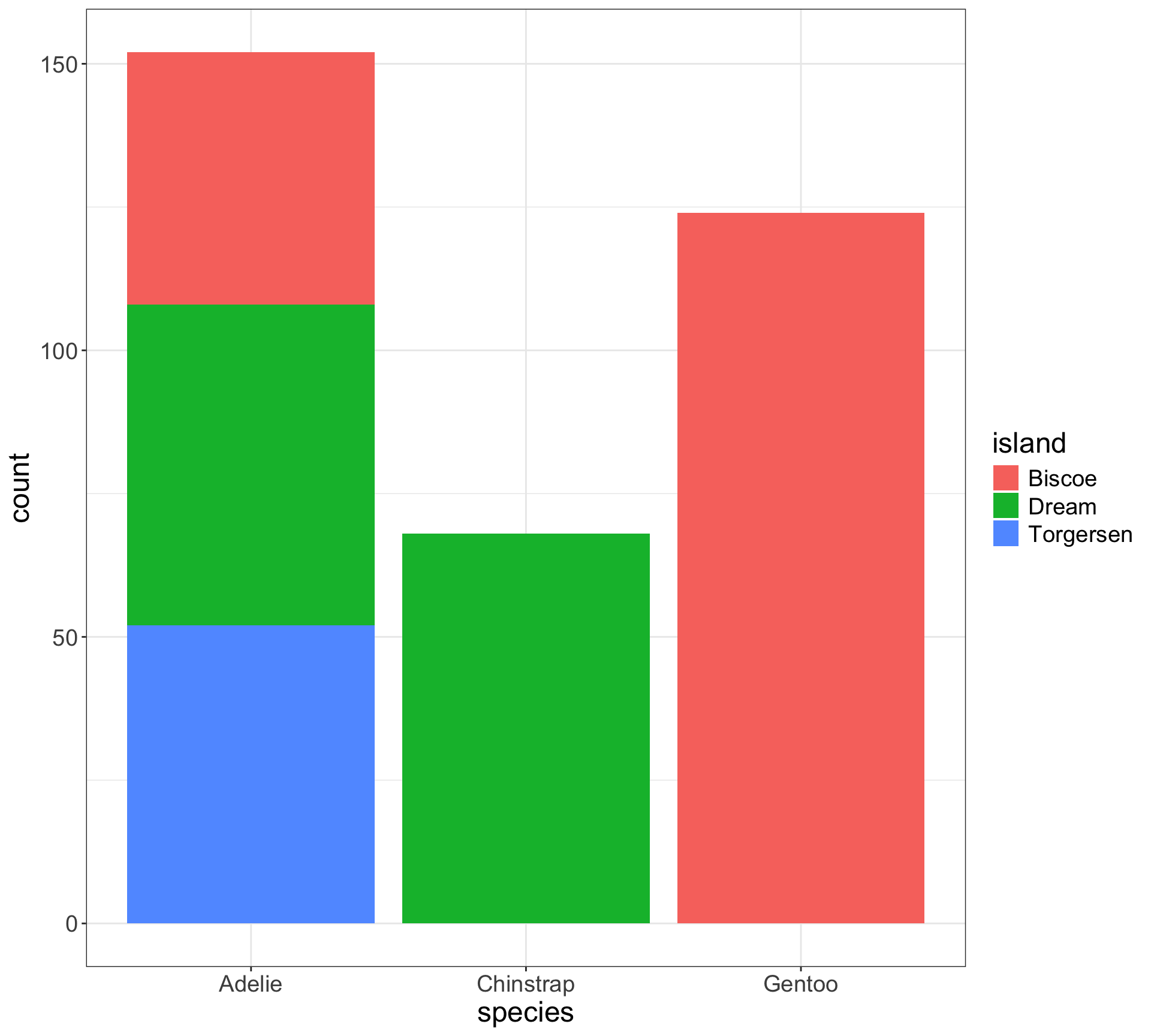
Stacked bar charts - a bar chart of spine charts

penguins |>
  ggplot(aes(x = species, fill = island)) +
  geom_bar() + 
  theme_bw()

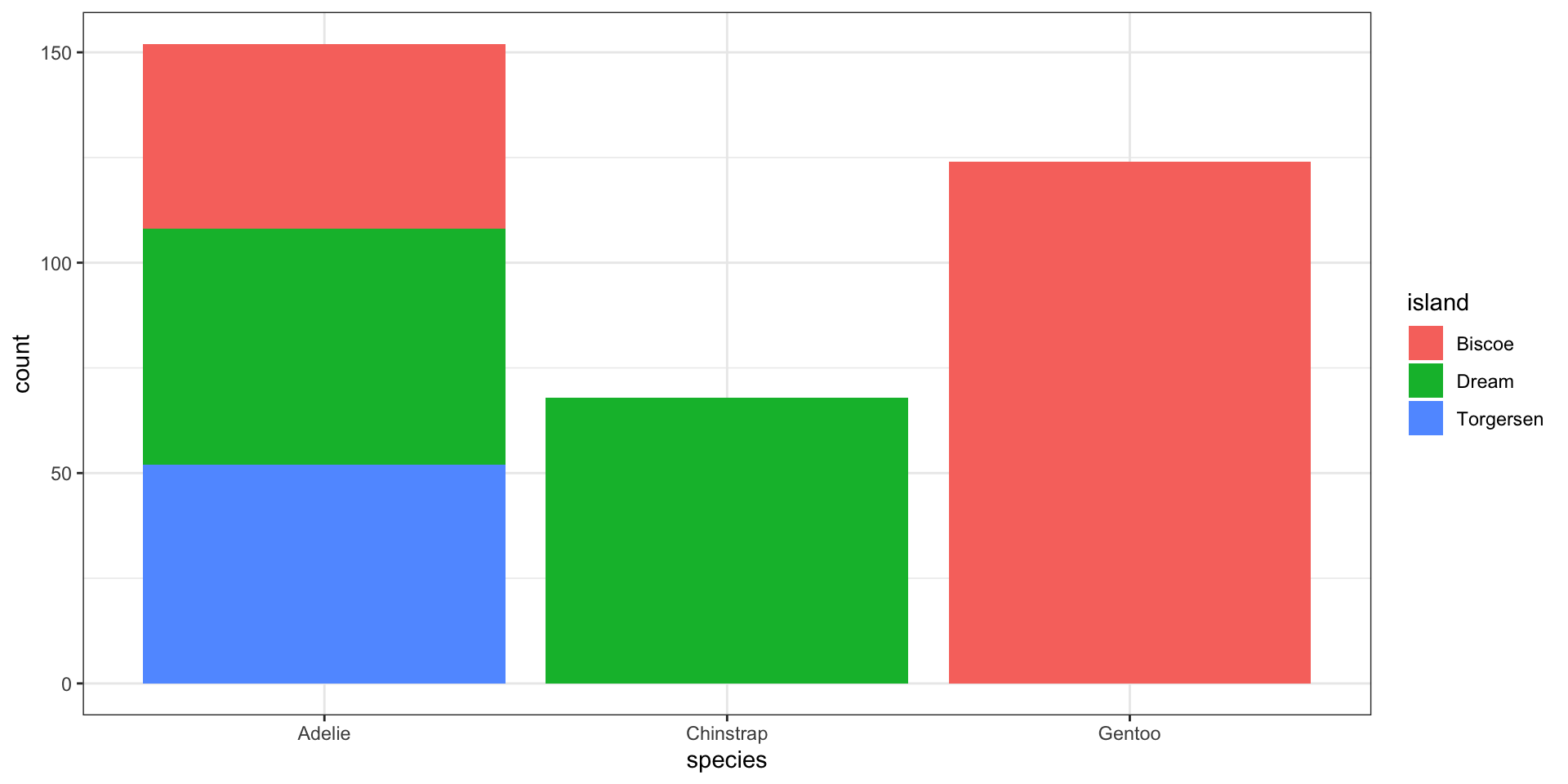
• Easy to see marginal of species, i.e., \(P(\) x \()\)

• Can see conditional of island | species, i.e., \(P(\) fill | x \()\)

• Harder to see conditional of species | island, i.e., \(P(\) x | fill \()\)

Side-by-side bar charts

penguins |>
  ggplot(aes(x = species, fill = island)) + 
  geom_bar(position = "dodge") +
  theme_bw()

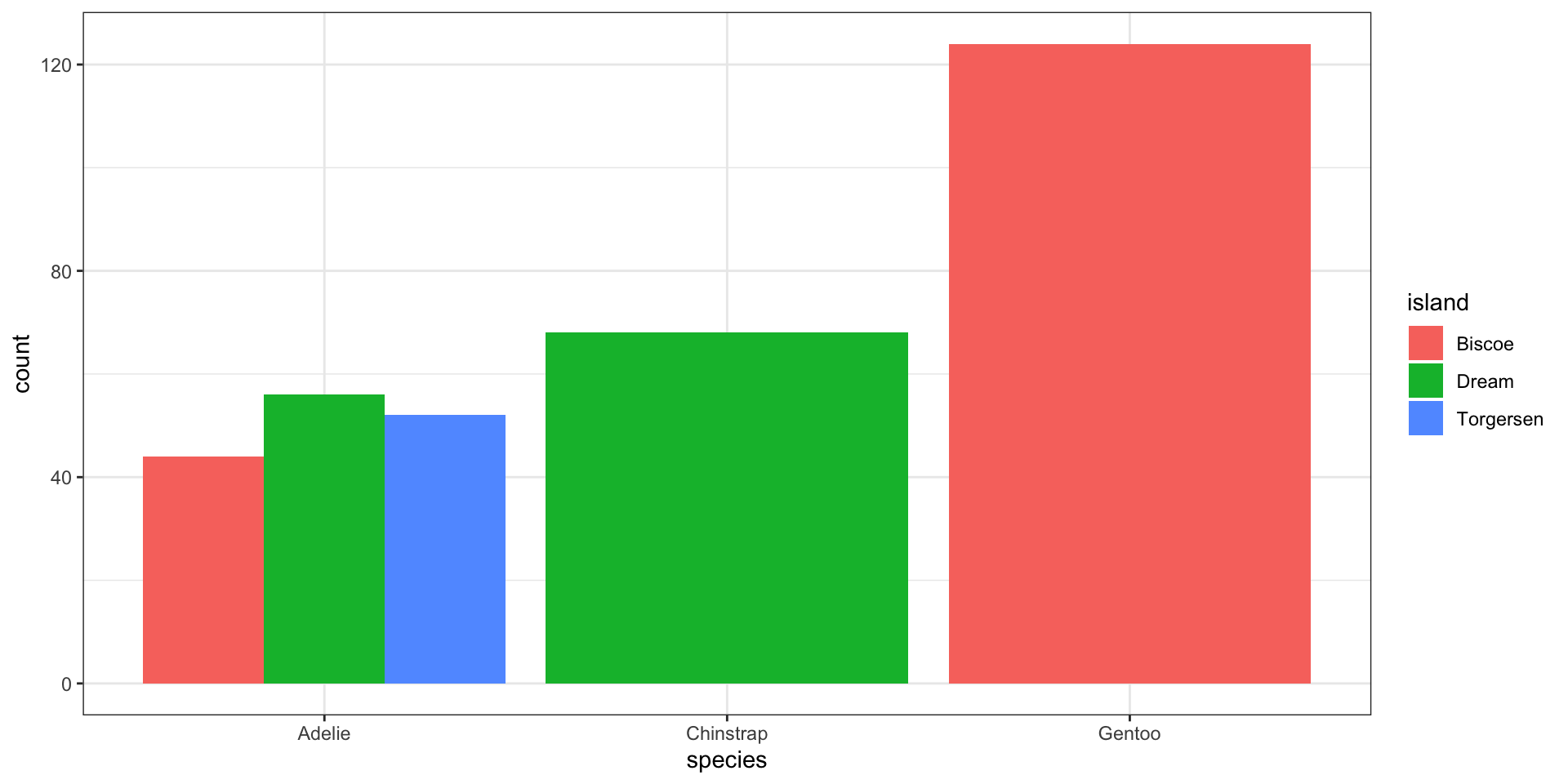
• Easy to see conditional of island | species, i.e., \(P(\) fill | x \()\)

• Can see conditional of species | island, i.e., \(P(\) x | fill \()\)

Side-by-side bar charts

penguins |>
  ggplot(aes(x = species, fill = island)) + 
  geom_bar(position = position_dodge(preserve = "single")) +
  theme_bw()

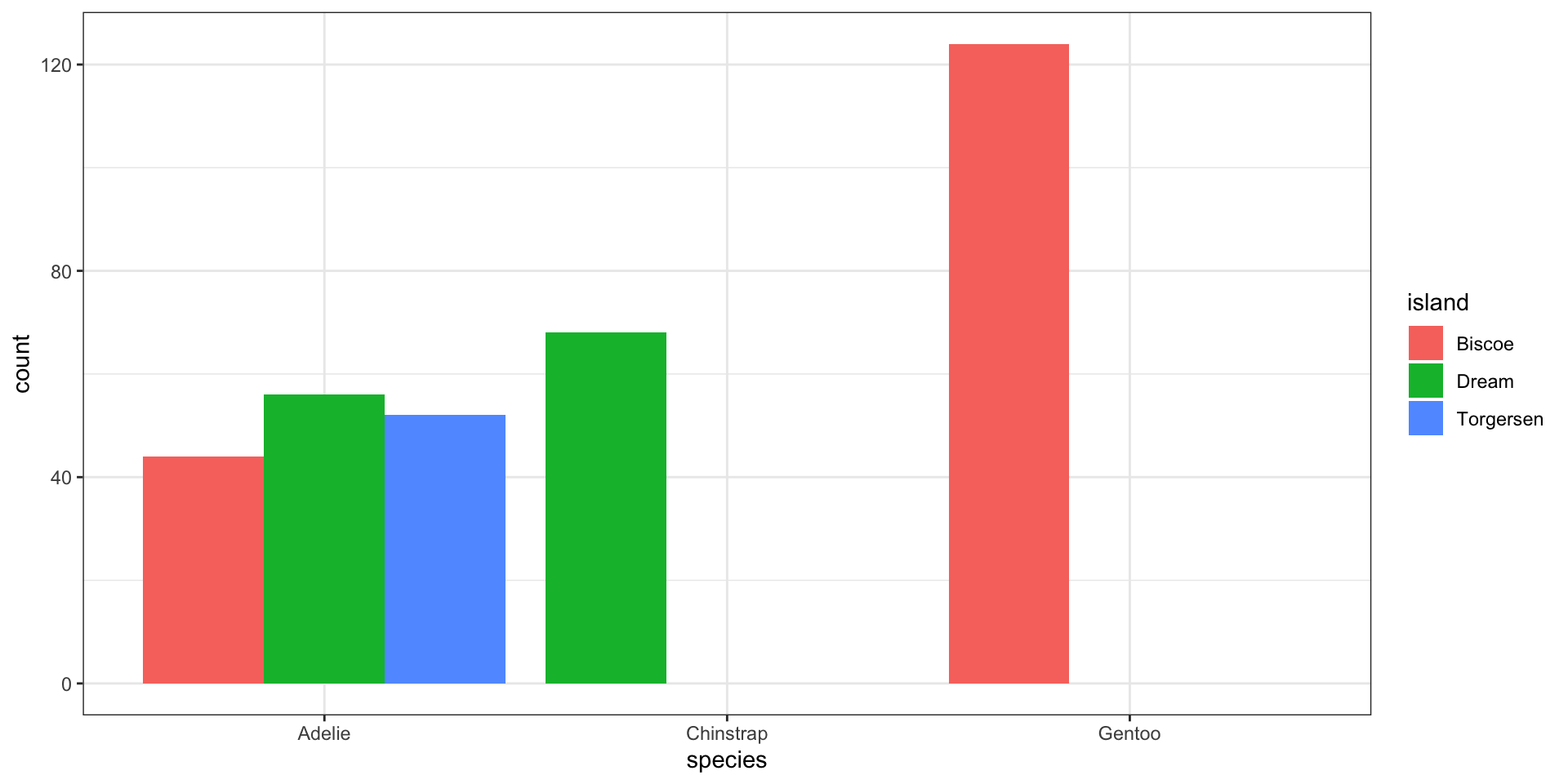
• Easy to see conditional of island | species, i.e., \(P(\) fill | x \()\)

• Can see conditional of species | island, i.e., \(P(\) x | fill \()\)

Complete missing values to preserve location

penguins |>
  count(species, island) |>
  complete(species = unique(species), island = unique(island), 
           fill = list(n = 0)) |>
  ggplot(aes(x = species, y = n, fill = island)) + 
  geom_bar(stat = "identity", position = "dodge") +
  theme_bw()

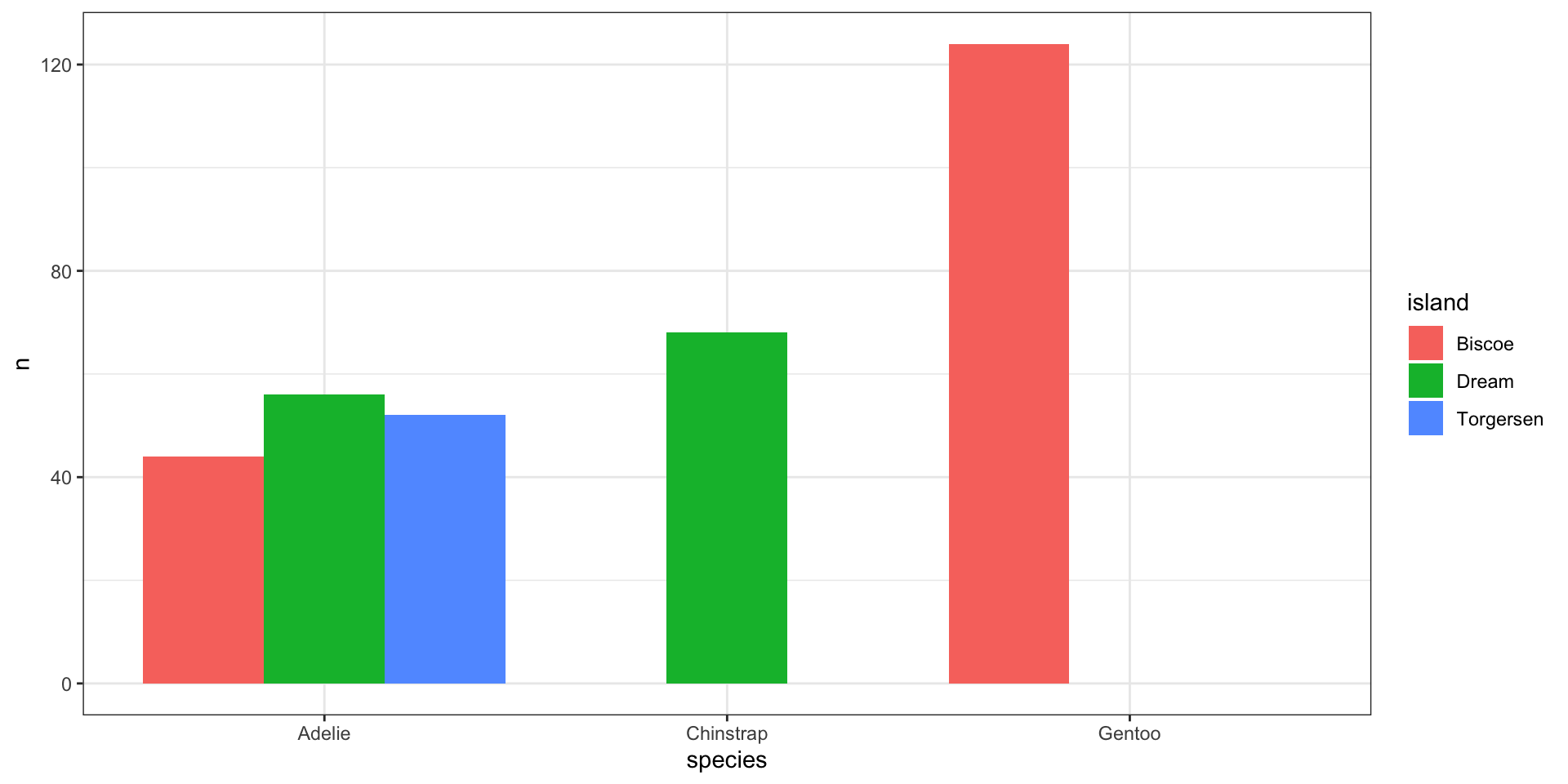
What do you prefer?

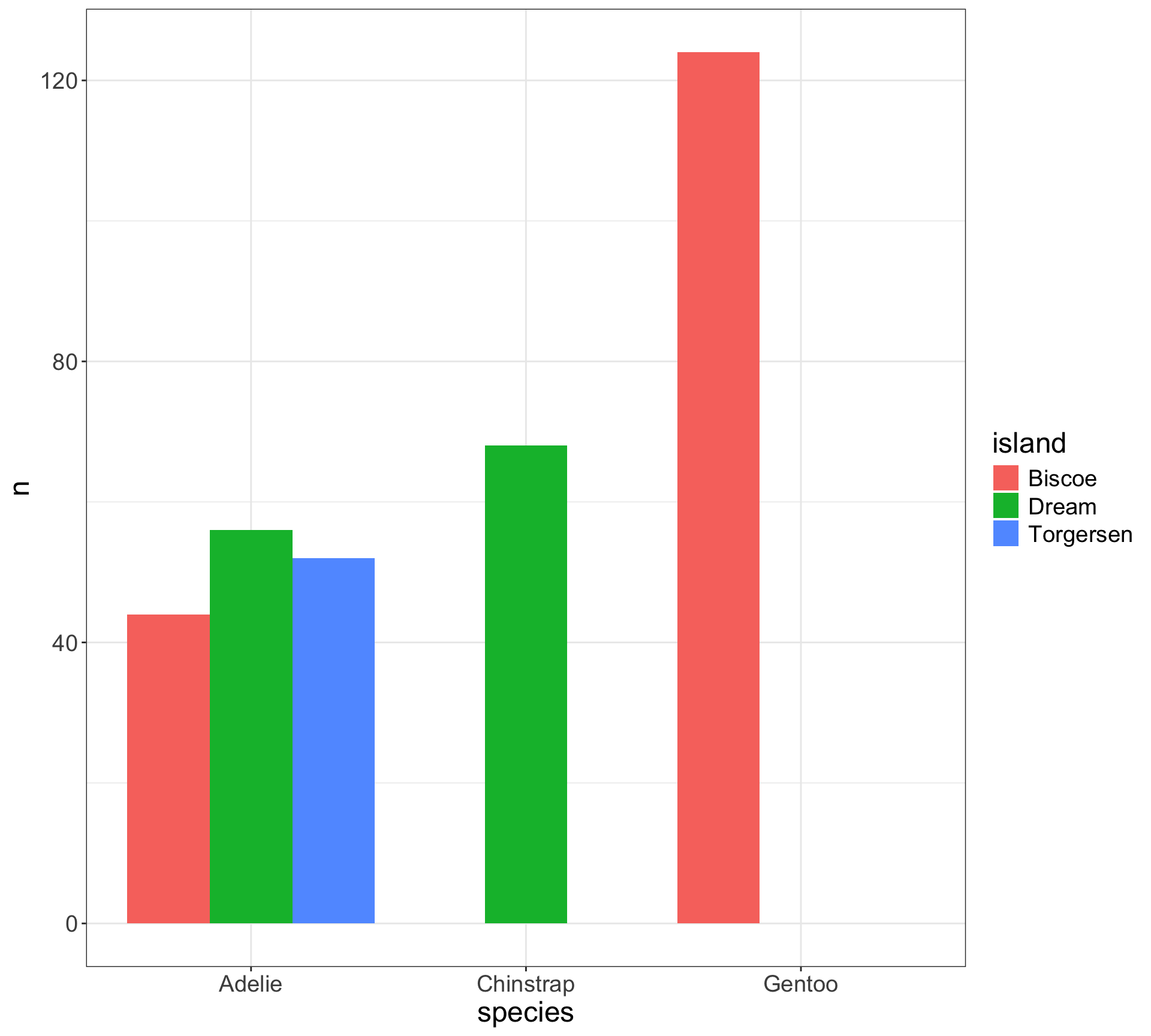
Chi-squared test for 1D categorical data:

• Null hypothesis \(H_0\): \(p_1 = p_2 = \dots = p_K\), compute the test statistic:

\[ \chi^2 = \sum_{j=1}^K \frac{(O_j - E_j)^2}{E_j} \]

• \(O_j\): observed counts in category \(j\)

• \(E_j\): expected counts under \(H_0\), i.e., each category is equally to occur \(n / K = p_1 = p_2 = \dots = p_K\)

chisq.test(table(penguins$species))

    Chi-squared test for given probabilities

data:  table(penguins$species)
X-squared = 31.907, df = 2, p-value = 1.179e-07

Hypothesis testing review

Computing \(p\)-values works like this:

• Choose a test statistic.

• Compute the test statistic in your dataset.

• Is test statistic “unusual” compared to what I would expect under \(H_0\)?

• Compare \(p\)-value to target error rate \(\alpha\) (typically referred to as target level \(\alpha\) )

• Typically choose \(\alpha = 0.05\)

  • i.e., if we reject null hypothesis at \(\alpha = 0.05\) then, assuming \(H_0\) is true, there is a 5% chance it is a false positive (aka Type 1 error)

Inference for 2D categorical data

Again we use the chi-squared test:

• Null hypothesis \(H_0\): variables \(A\) and \(B\) are independent, compute the test statistic:

\[\chi^2 = \sum_{i}^{K_A} \sum_{j}^{K_B} \frac{(O_{ij} - E_{ij})^2}{E_{ij}}\]

• \(O_{ij}\): observed counts in contingency table

• \(E_{ij}\): expected counts under \(H_0\)

\[ \begin{aligned} E_{ij} &= n \cdot P(A = a_i, B = b_j) \\ &= n \cdot P(A = a_i) P(B = b_j) \\ &= n \cdot \left( \frac{n_{i \cdot}}{n} \right) \left( \frac{ n_{\cdot j}}{n} \right) \end{aligned} \]

Inference for 2D categorical data

Again we use the chi-squared test:

• Null hypothesis \(H_0\): variables \(A\) and \(B\) are independent, compute the test statistic:

\[\chi^2 = \sum_{i}^{K_A} \sum_{j}^{K_B} \frac{(O_{ij} - E_{ij})^2}{E_{ij}}\]

• \(O_{ij}\): observed counts in contingency table

• \(E_{ij}\): expected counts under \(H_0\)

chisq.test(table(penguins$species, penguins$island))

    Pearson's Chi-squared test

data:  table(penguins$species, penguins$island)
X-squared = 299.55, df = 4, p-value < 2.2e-16

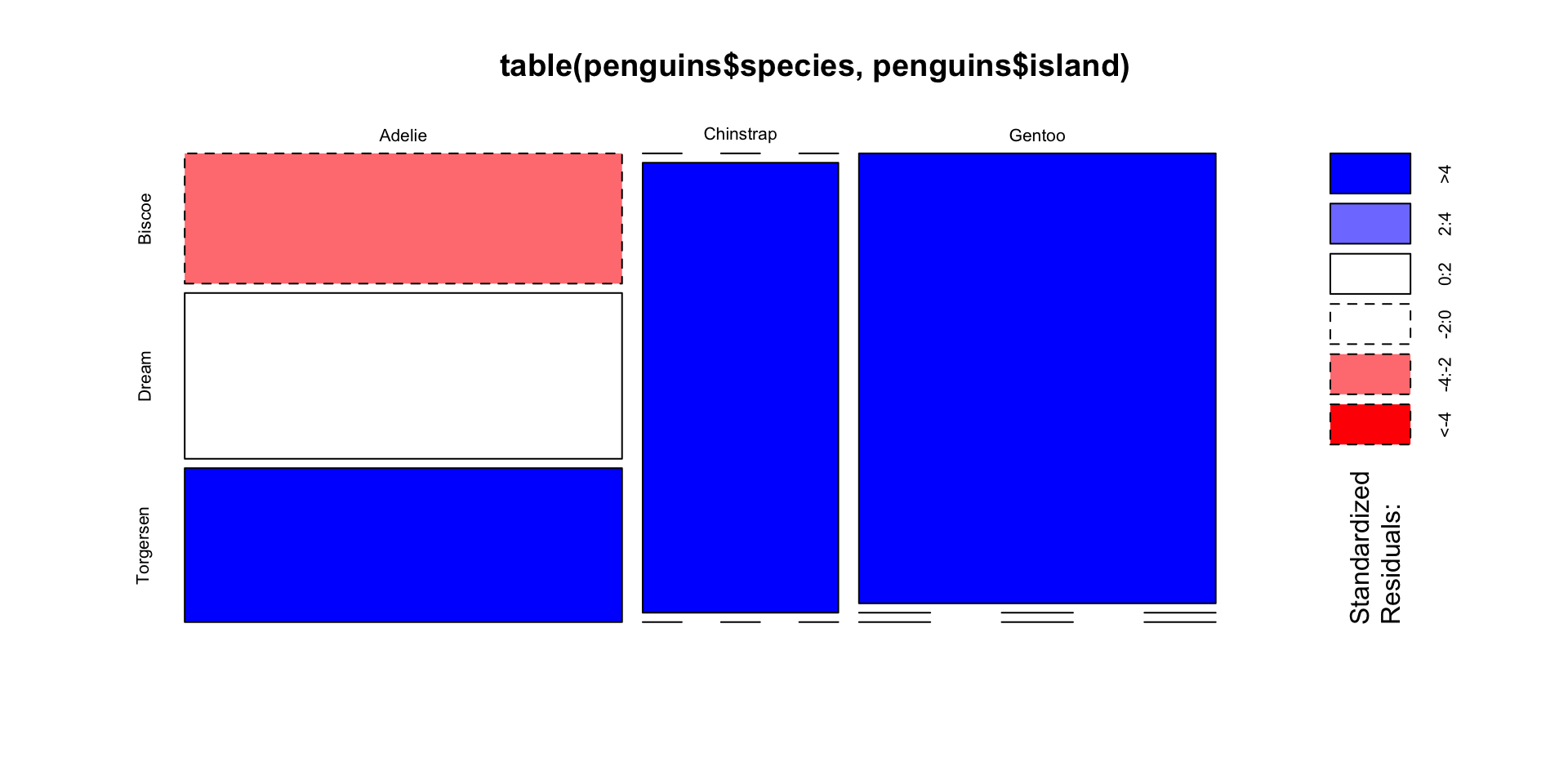
Visualize independence test with mosaic plots

Two variables are independent if knowing the level of one tells us nothing about the other

• i.e. \(P(A | B) = P(A)\), and that \(P(A, B) = P(A) \times P(B)\)

Create a mosaic plot using base R

mosaicplot(table(penguins$species, penguins$island)) 

Shade by Pearson residuals

• The test statistic is:

\[\chi^2 = \sum_{i}^{K_A} \sum_{j}^{K_B} \frac{(O_{ij} - E_{ij})^2}{E_{ij}}\]

• Define the Pearson residuals as:

\[r_{ij} = \frac{O_{ij} - E_{ij}}{\sqrt{E_{ij}}}\]

• Side-note: In general, Pearson residuals are \(\frac{\text{residuals}}{\sqrt{\text{variance}}}\)

• \(r_{ij} \approx 0 \rightarrow\) observed counts are close to expected counts

• \(|r_{ij}| > 2 \rightarrow\) “significant” at level \(\alpha = 0.05\).

• Very positive \(r_{ij} \rightarrow\) more than expected, while very negative \(r_{ij} \rightarrow\) fewer than expected

• Color by Pearson residuals to tell us which combos are much bigger/smaller than expected.

mosaicplot(table(penguins$species, penguins$island), shade = TRUE)

mosaicplot(table(penguins$island, penguins$sex), shade = TRUE,
           main = "Distribution of penguins' sex does not vary across islands")

Bonus: Treemaps do not require same categorical levels across subgroups

library(treemapify)
penguins |>
  group_by(species, island) |>
  summarize(count = n(), .groups = "drop") |>
  ggplot(aes(area = count, subgroup = island,
             label = species,
             fill = interaction(species, island))) +
  # 1. Draw species borders and fill colors
  geom_treemap() +
  # 2. Draw island borders
  geom_treemap_subgroup_border() +
  # 3. Print island text
  geom_treemap_subgroup_text(place = "centre", grow = T, 
                             alpha = 0.5, colour = "black",
                             fontface = "italic", min.size = 0) +
  # 4. Print species text
  geom_treemap_text(colour = "white", place = "topleft", 
                    reflow = T) +
  guides(colour = "none", fill = "none")

Bonus: Treemaps do not require same categorical levels across subgroups

1D Quantitative Data

Observations are collected into a vector \((x_1, \dots, x_n)\), \(x_i \in \mathbb{R}\) (or \(\mathbb{R}^+\), \(\mathbb{Z}\))

Common summary statistics for 1D quantitative data:

• Center: Mean, median, weighted mean, mode

  • Related to the first moment, i.e., \(\mathbb{E}[X]\)

• Spread: Variance, range, min/max, quantiles, IQR

  • Related to the second moment, i.e., \(\mathbb{E}[X^2]\)

• Shape: symmetry, skew, kurtosis (“peakedness”)

  • Related to higher order moments, i.e., skewness is \(\mathbb{E}[X^3]\), kurtosis is \(\mathbb{E}[X^4]\)

Compute various statistics with summary(), mean(), median(), quantile(), range(), sd(), var(), etc.

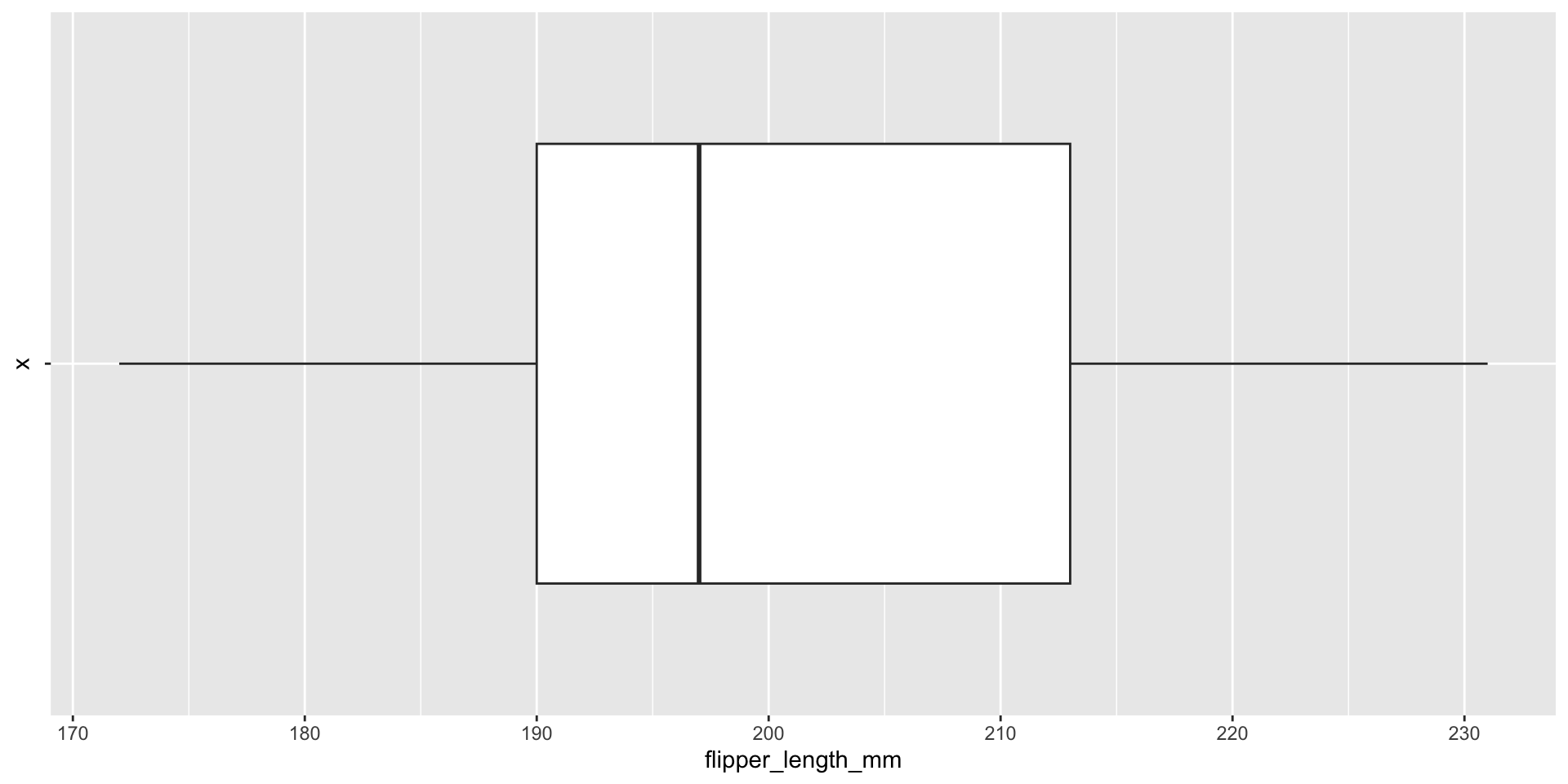
Box plots visualize summary statistics

penguins |>
  ggplot(aes(y = flipper_length_mm)) +
  geom_boxplot(aes(x = "")) +
  coord_flip()

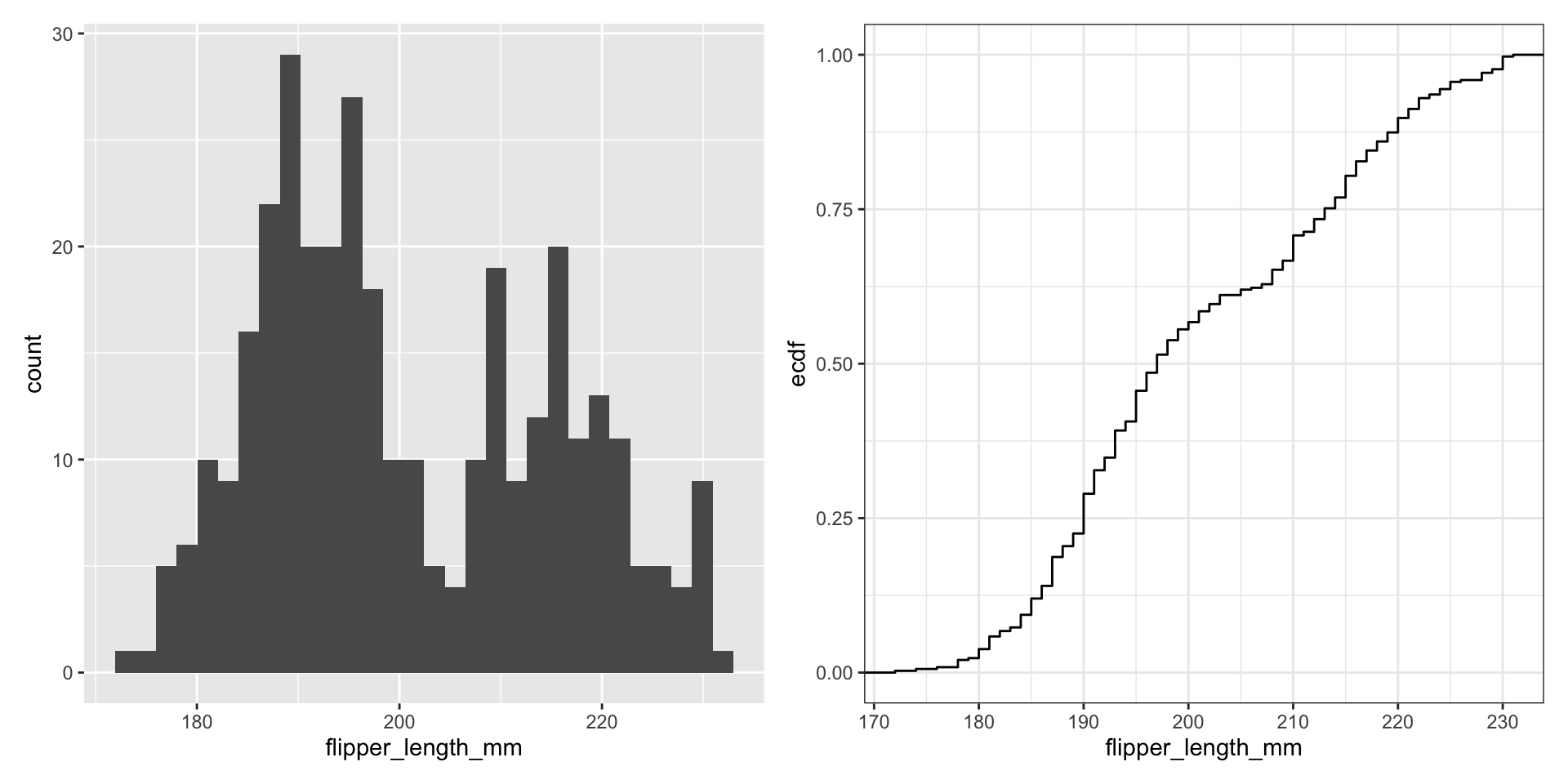
Histograms display 1D continuous distributions

penguins |>
  ggplot(aes(x = flipper_length_mm)) +
  geom_histogram()

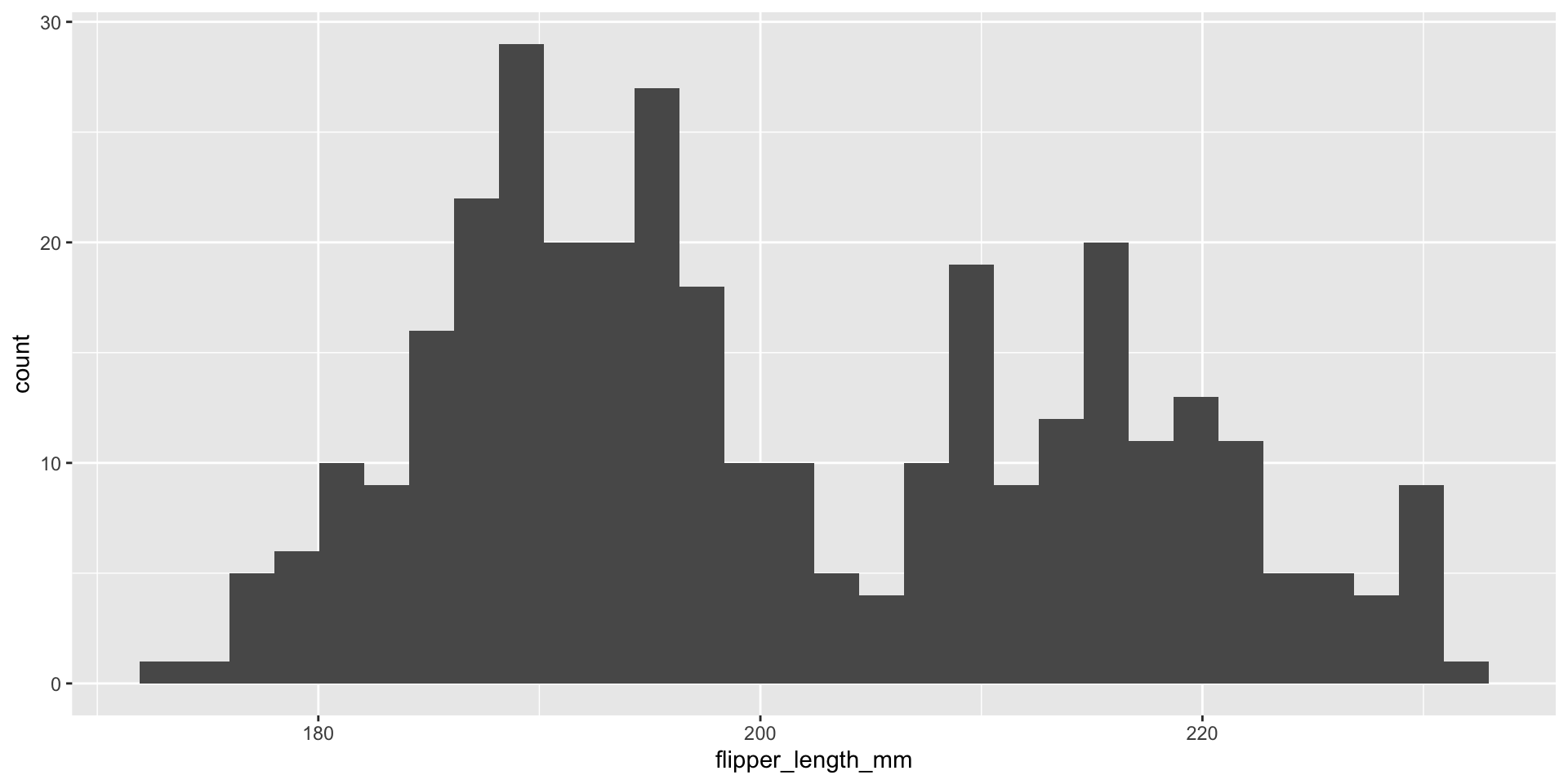
Do NOT rely on box plots…

What do visualizations of continuous distributions display?

Probability that continuous variable \(X\) takes a particular value is 0

e.g., \(P\) (flipper_length_mm \(= 200\)) \(= 0\), why?

Instead we use the probability density function (PDF) to provide a relative likelihood

For continuous variables we can use the cumulative distribution function (CDF),

\[ F(x) = P(X \leq x) \]

For \(n\) observations we can easily compute the Empirical CDF (ECDF):

\[\hat{F}_n(x) = \frac{\text{# obs. with variable} \leq x}{n} = \frac{1}{n} \sum_{i=1}^{n}1(x_i \leq x)\]

• where \(1()\) is the indicator function, i.e. ifelse(x_i <= x, 1, 0)

Display full distribution with ECDF plot

penguins |>
  ggplot(aes(x = flipper_length_mm)) + 
  stat_ecdf() +
  theme_bw()

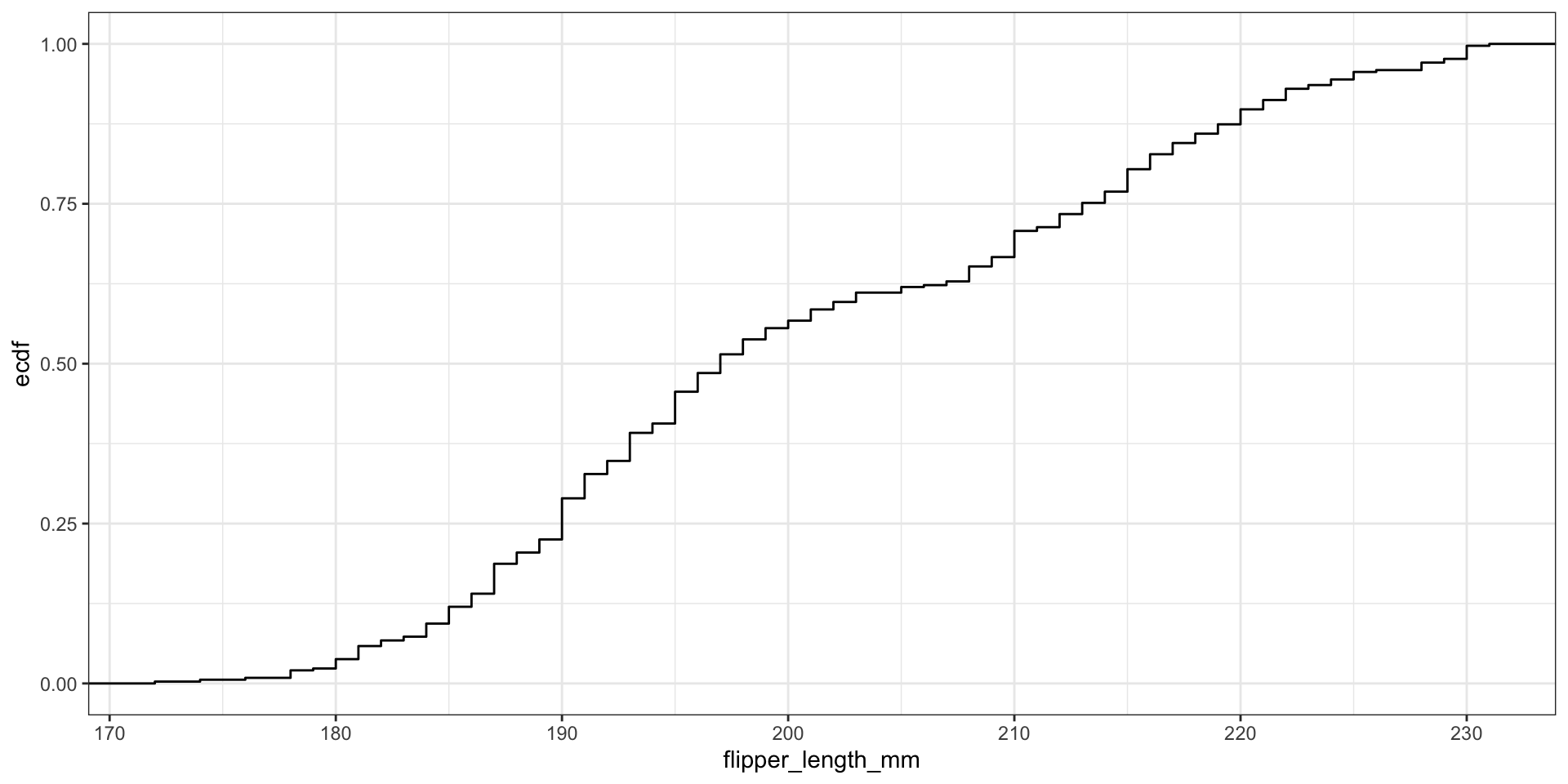
What’s the relationship between these two figures?

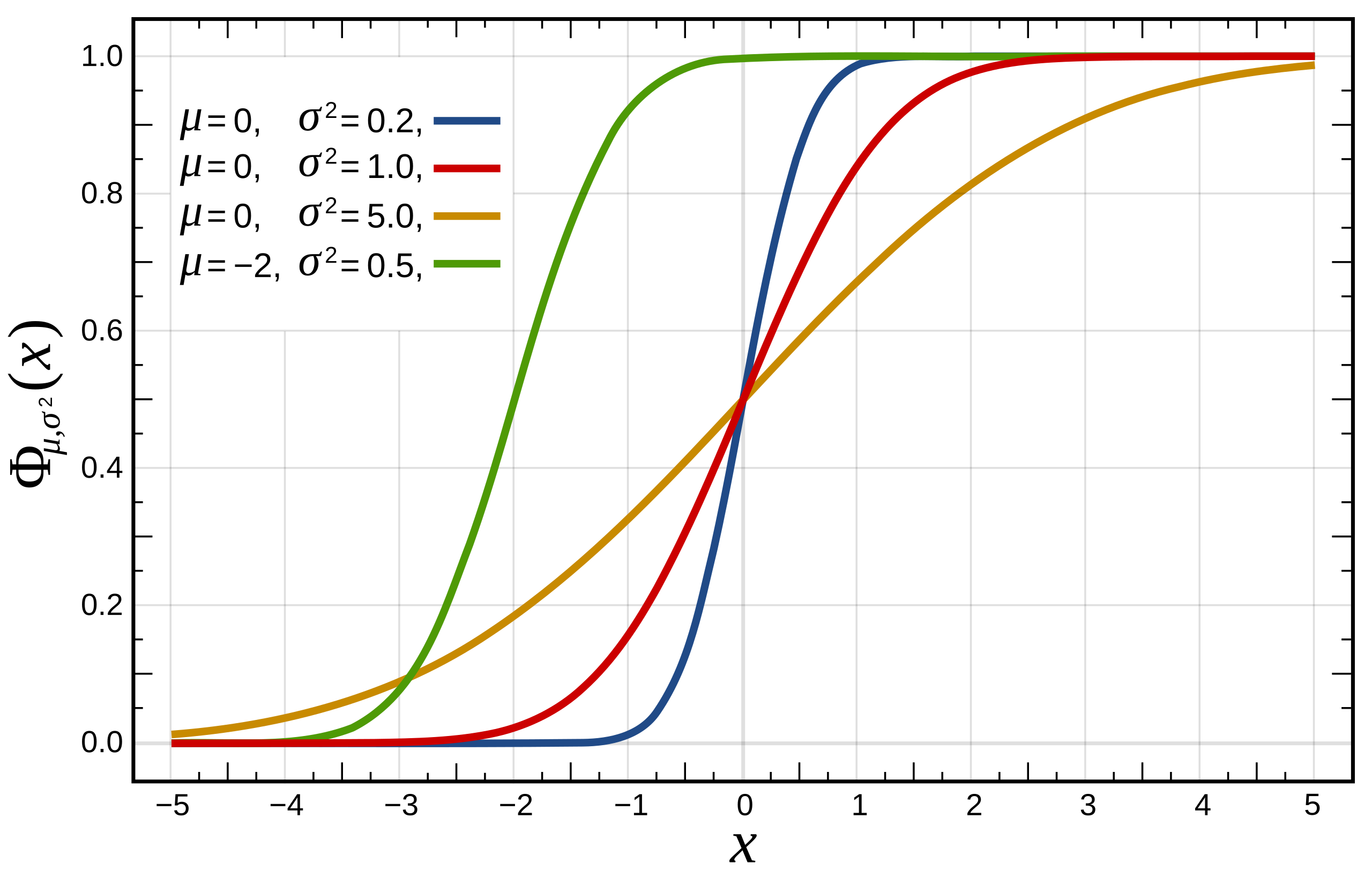
What about comparing to theoretical distributions?

One-Sample Kolmogorov-Smirnov Test

• We compare the ECDF \(\hat{F}(x)\) to a theoretical distribution’s CDF \(F(x)\)

• The one sample KS test statistic is: \(\text{max}_x |\hat{F}(x) - F(x)|\)

Flipper length example

What if we assume flipper_length_mm follows Normal distribution?

• i.e., flipper_length_mm \(\sim N(\mu, \sigma^2)\)

Need estimates for mean \(\mu\) and standard deviation \(\sigma\):

flipper_length_mean <- mean(penguins$flipper_length_mm, na.rm = TRUE)
flipper_length_sd <- sd(penguins$flipper_length_mm, na.rm = TRUE)

Perform one-sample KS test using ks.test():

ks.test(x = penguins$flipper_length_mm, y = "pnorm",
        mean = flipper_length_mean, sd = flipper_length_sd)

    Asymptotic one-sample Kolmogorov-Smirnov test

data:  penguins$flipper_length_mm
D = 0.12428, p-value = 5.163e-05
alternative hypothesis: two-sided

Flipper length example

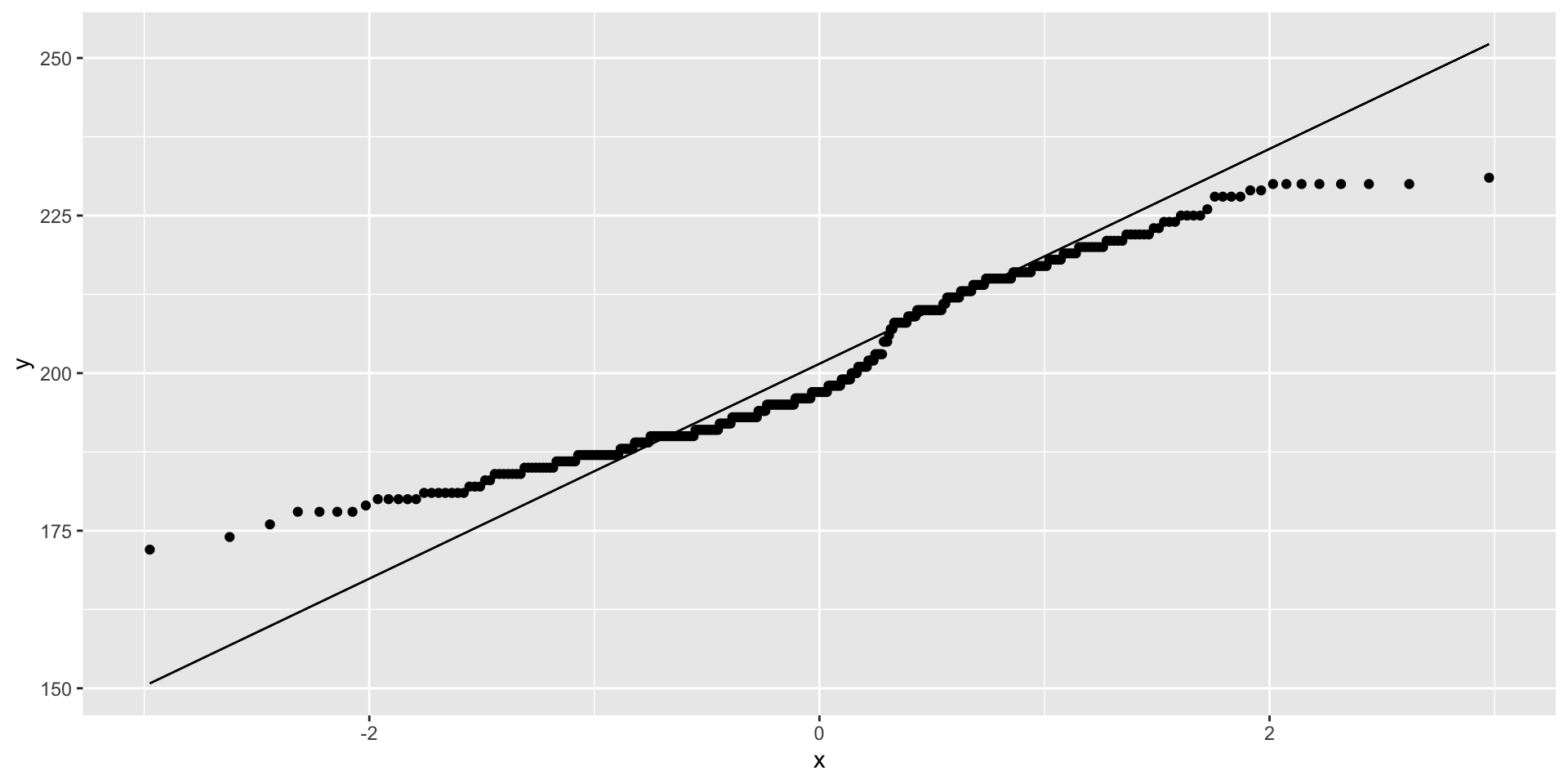
Visualize distribution comparisons using quantile-quantile (q-q) plots

penguins |>
  ggplot(aes(sample = flipper_length_mm)) +
  stat_qq() +
  stat_qq_line()

Recap and next steps

• Visualize categorical data with bars! Regular, stacked, side-by-side, mosaic

• Display uncertainty: (1D) standard errors, (2D) Pearson residuals

• Visualize 1D quantitative data with histograms, ECDFs, but never use a box plot by itself

• HW1 is due TONIGHT!

• HW2 is posted (due next Wednesday)

• Next time: Density Estimation

• Recommended reading:

• CW Chapter 11 Visualizing nested proportions, CW Chapter 7 Visualizing distributions: Histograms and density plots, CW Chapter 8 Visualizing distributions: Empirical cumulative distribution functions and q-q plots

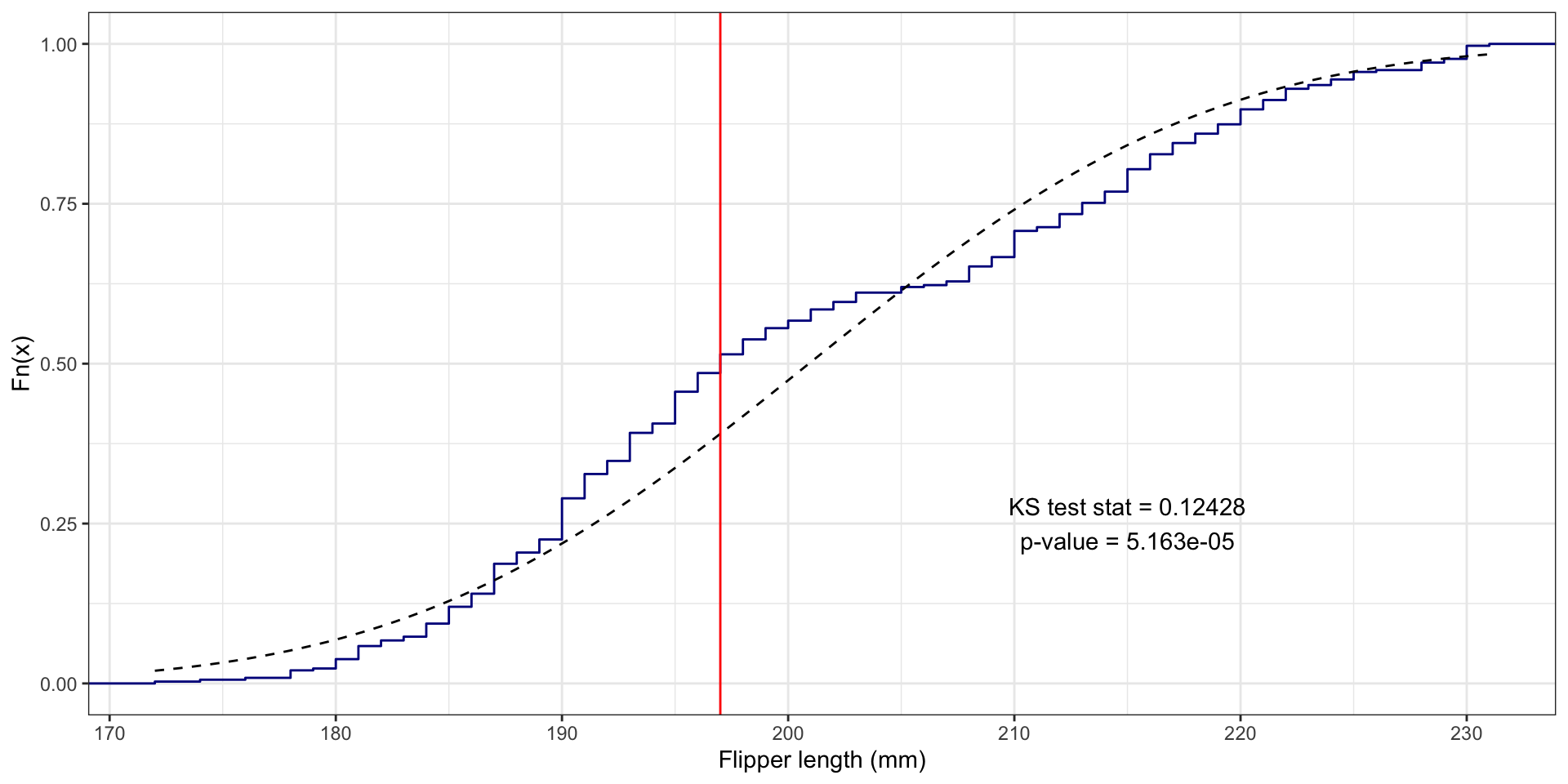
BONUS: Visualizing the KS test statistic

# First create the ECDF function for the variable:
fl_ecdf <- ecdf(penguins$flipper_length_mm)
# Compute the absolute value of the differences between the ECDF for the values
# and the theoretical values with assumed Normal distribution:
abs_ecdf_diffs <- abs(fl_ecdf(penguins$flipper_length_mm) - pnorm(penguins$flipper_length_mm,
                                                                  mean = flipper_length_mean, sd = flipper_length_sd))
# Now find where the maximum difference is:
max_abs_ecdf_diff_i <- which.max(abs_ecdf_diffs)
# Get this flipper length value:
max_fl_diff_value <- penguins$flipper_length_mm[max_abs_ecdf_diff_i]
# Plot the ECDF with the theoretical Normal and KS test info:
penguins |>
  ggplot(aes(x = flipper_length_mm)) +
  stat_ecdf(color = "darkblue") +
  # Use stat_function to draw the Normal ECDF
  stat_function(fun = pnorm, args = list(mean = flipper_length_mean, sd = flipper_length_sd), color = "black", linetype = "dashed") +
  # Draw KS test line:
  geom_vline(xintercept = max_fl_diff_value, color = "red") +
  # Add text with the test results (x and y are manually entered locations)
  annotate(geom = "text", x = 215, y = .25, label = "KS test stat = 0.12428\np-value = 5.163e-05") + 
  labs(x = "Flipper length (mm)", y = "Fn(x)") + theme_bw()