Visualizing Quantitative Distributions
2024-09-09
Reminders, previously, and today…
HW2 is due Wednesday Sept 11th!
HW3 is posted and due next Wednesday Sept 18th
Visualized 2D categorical data with more bar charts, include mosaic plots
Walked through different approaches for 1D quantitative data visualization
TODAY:
Thinking carefully about histograms
Introduction to density estimation
Visualization 1D quantitative by 1D categorical distributions
Simulate data from mixture of Normal distributions
Will sample 100 draws from \(N(-1.5, 1)\) and 100 draws from \(N(1.5, 1)\)
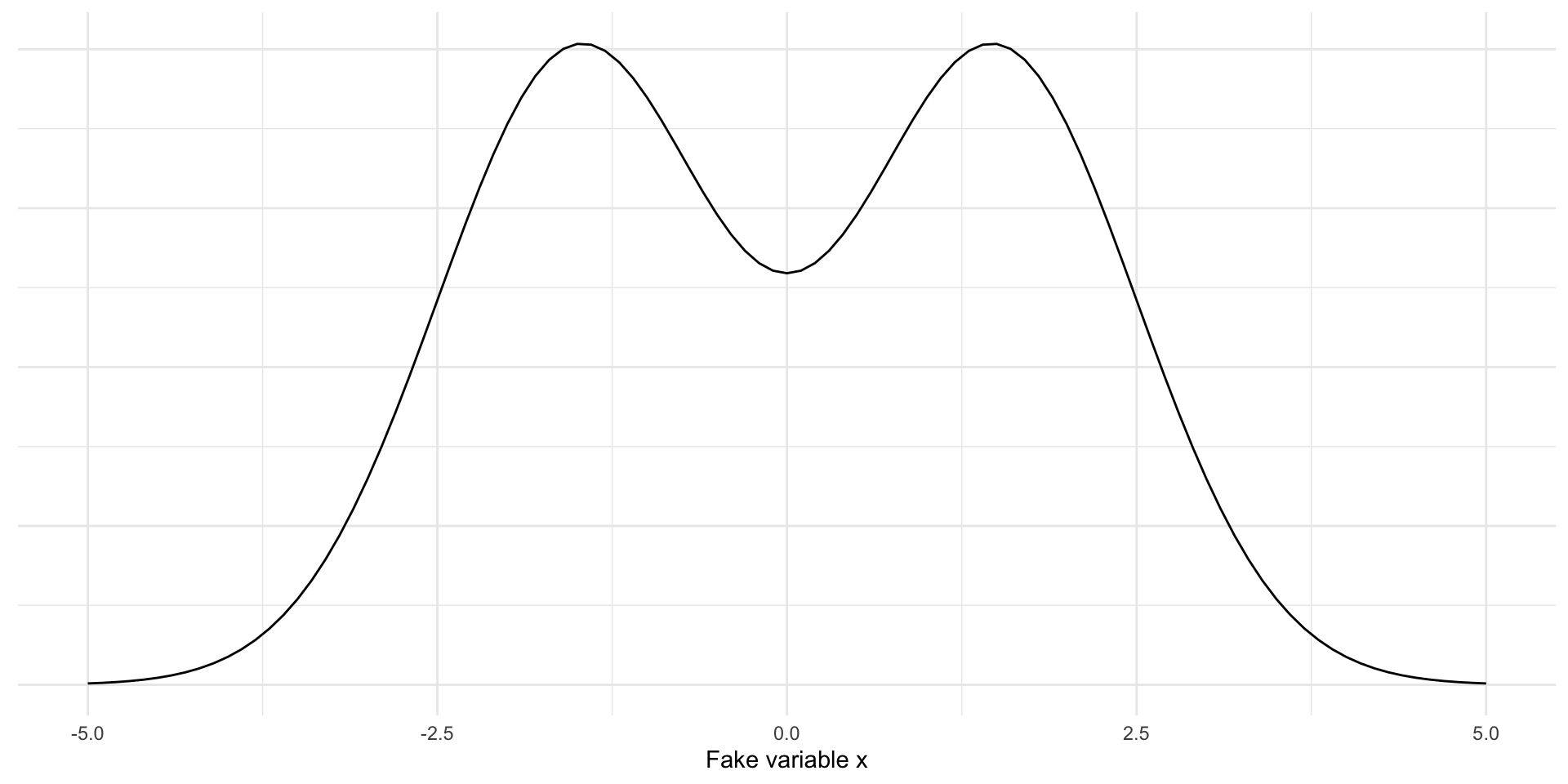
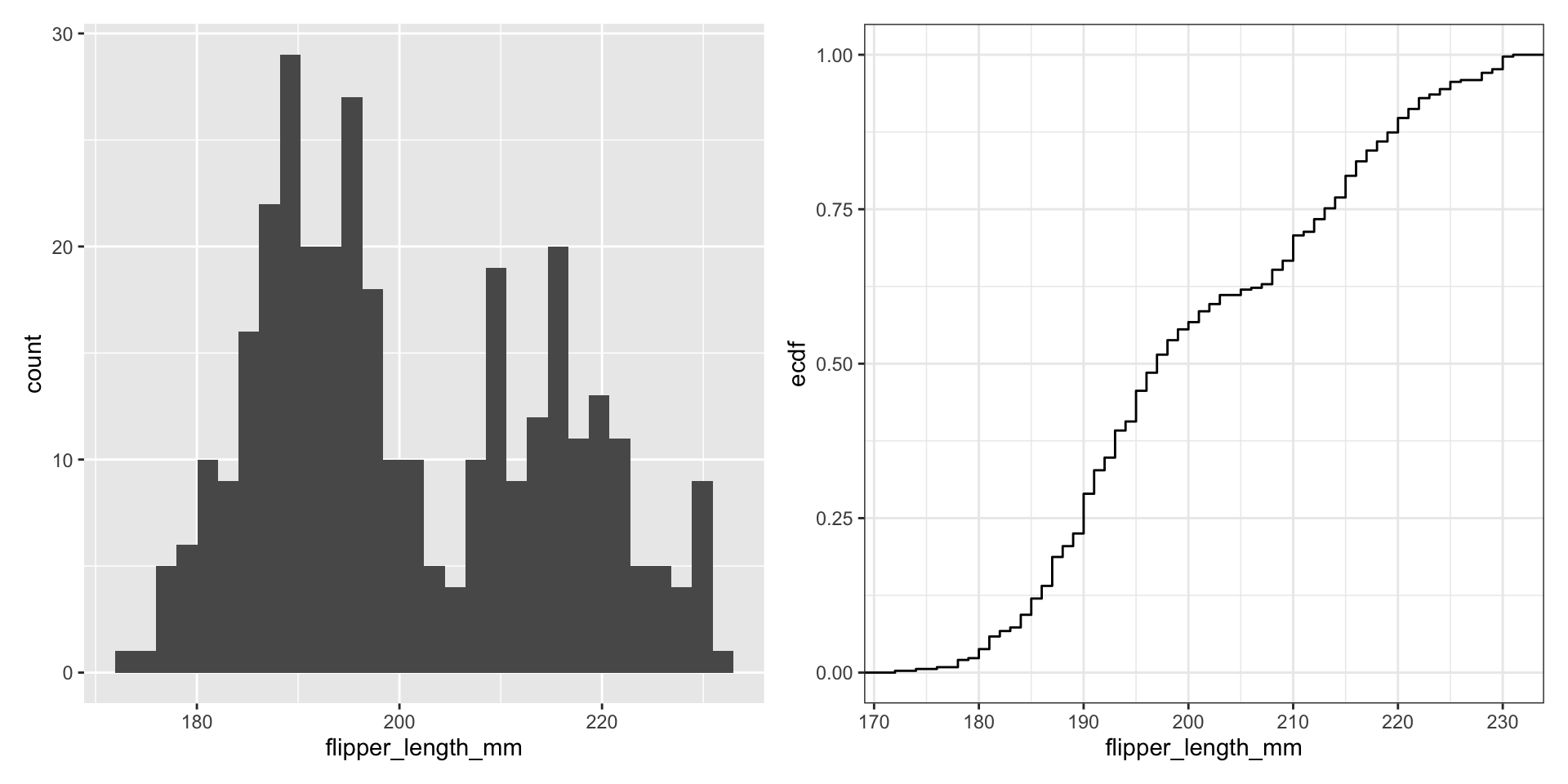
Revisit histograms
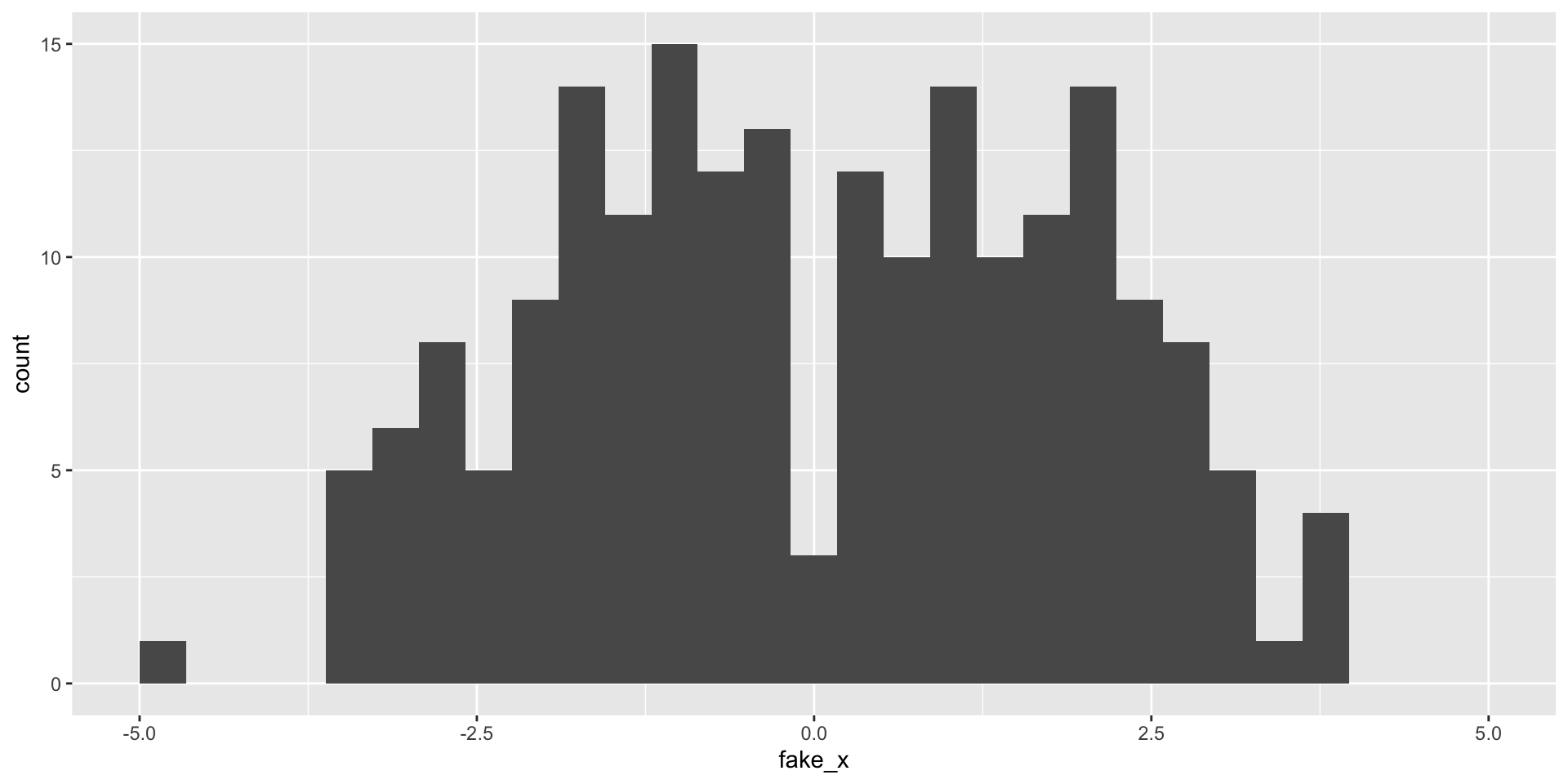
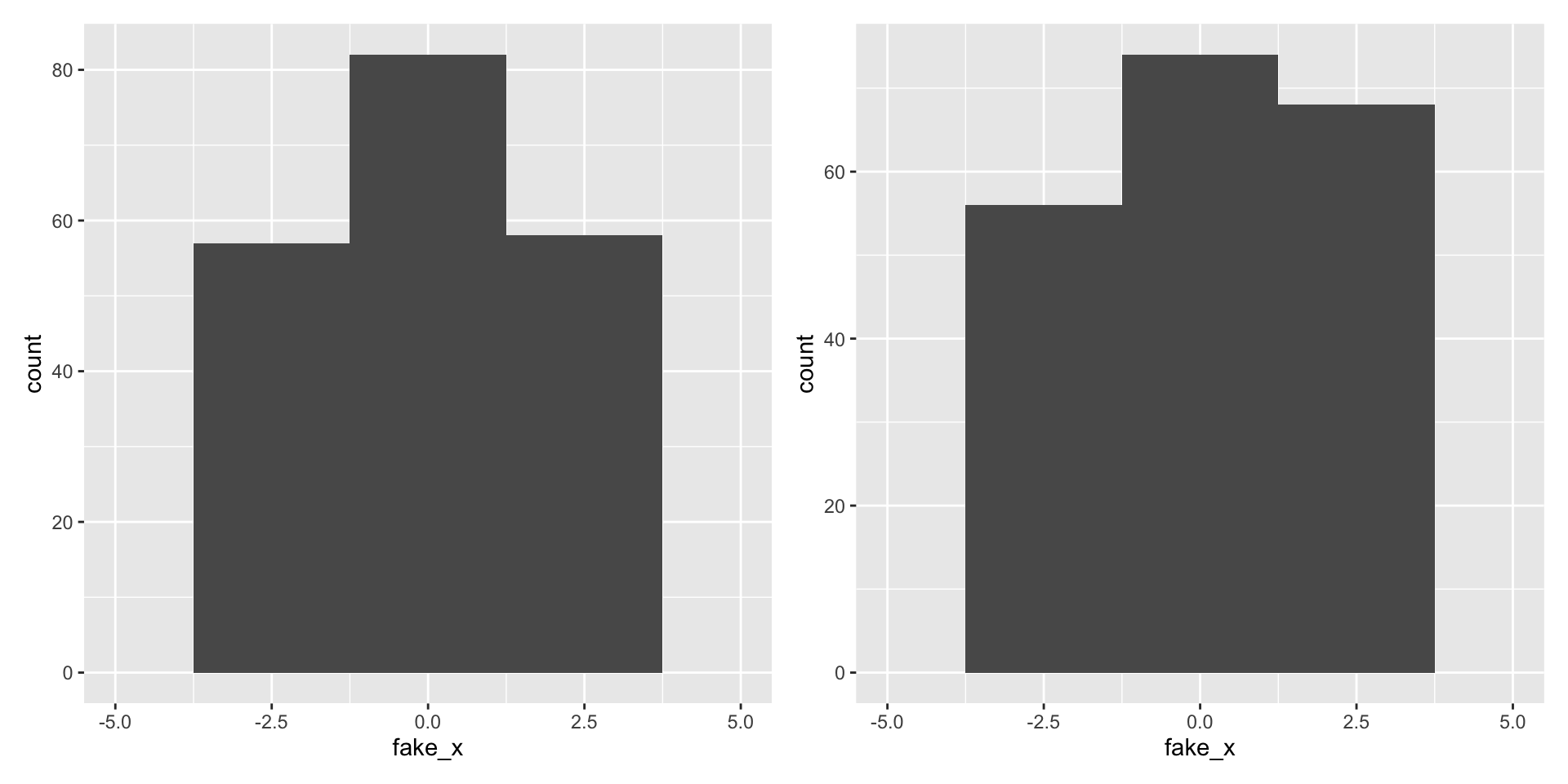
What happens as we change the number of bins?
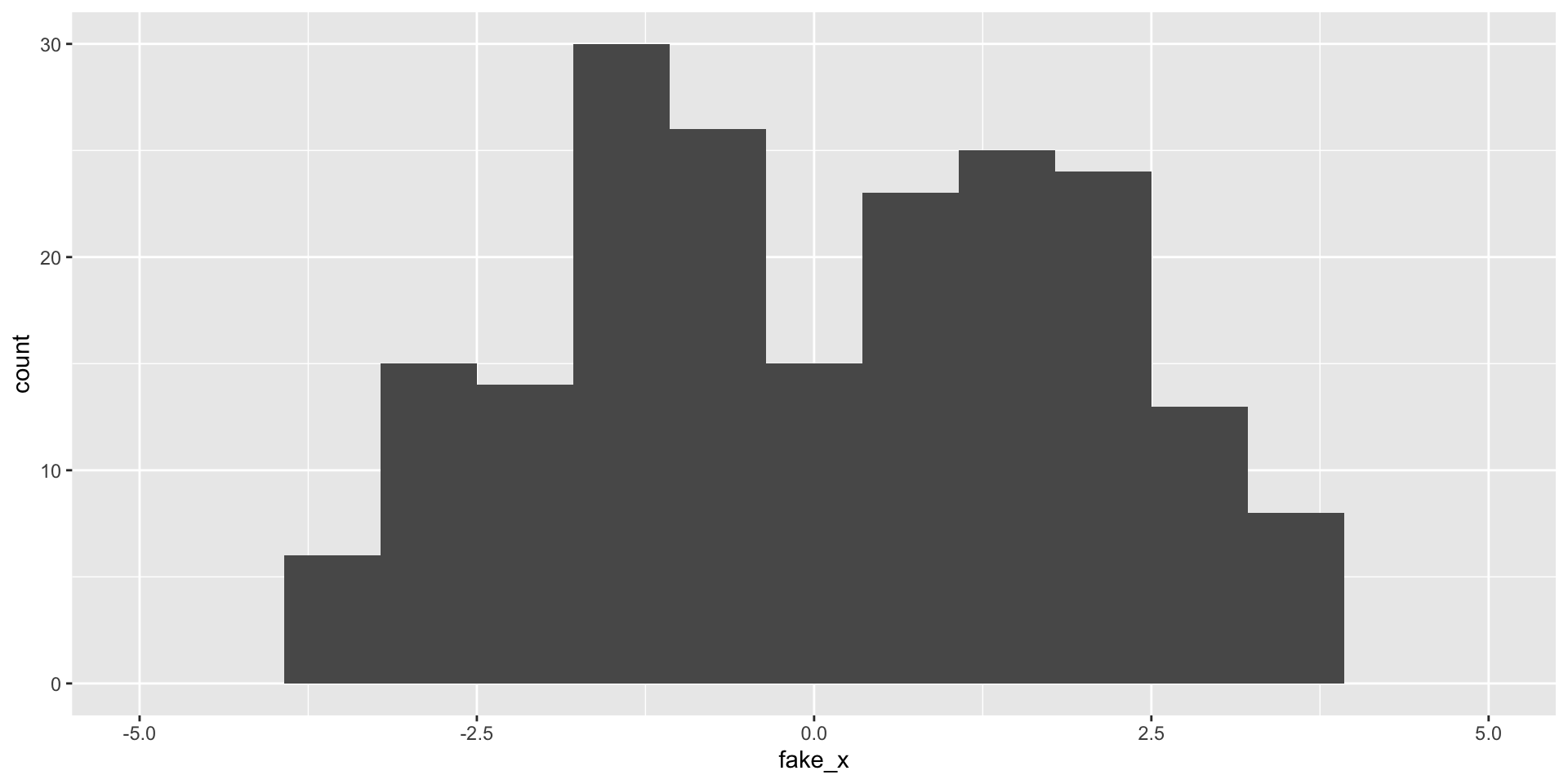
What happens as we change the number of bins?
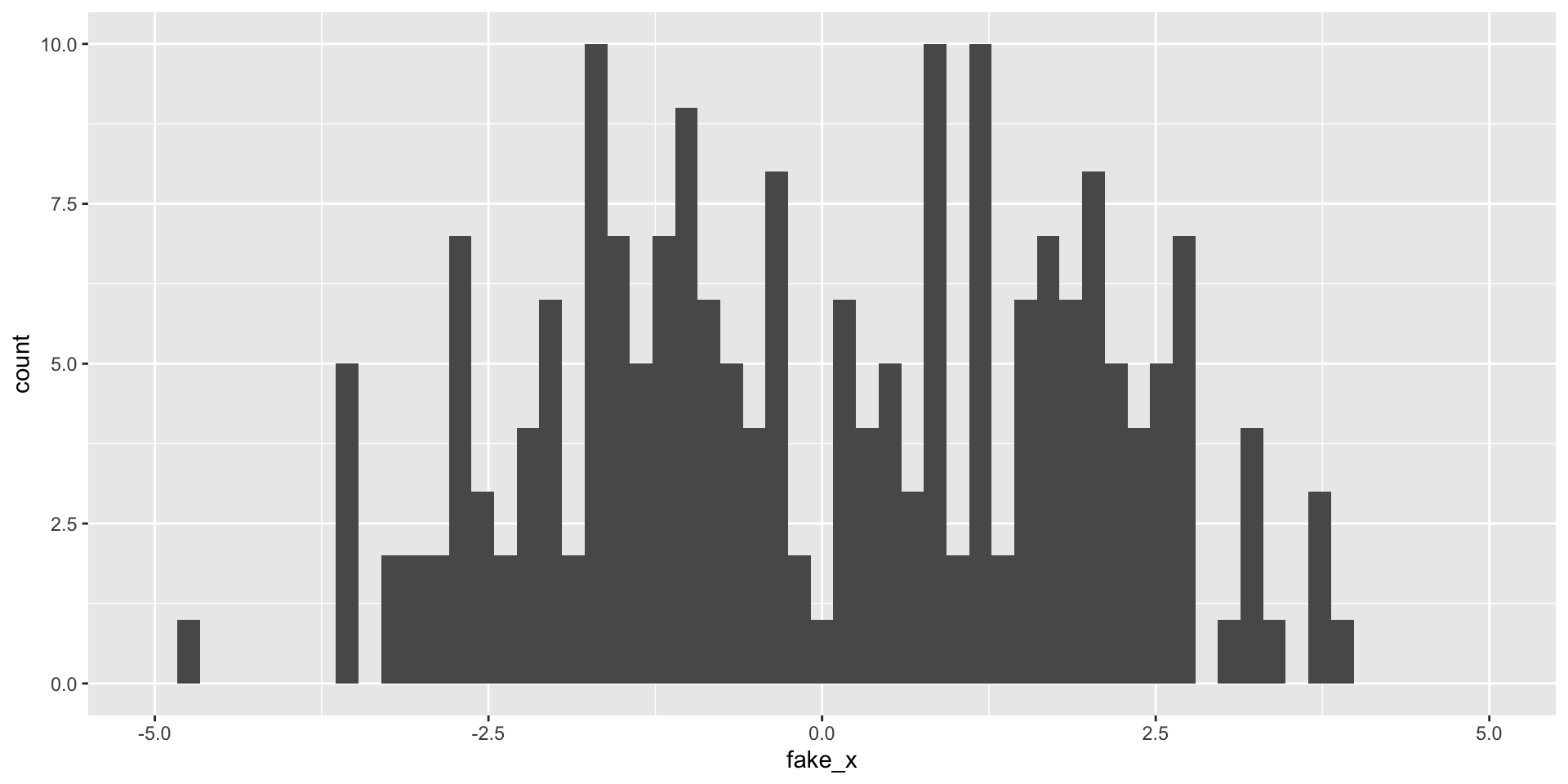
What happens as we change the number of bins?
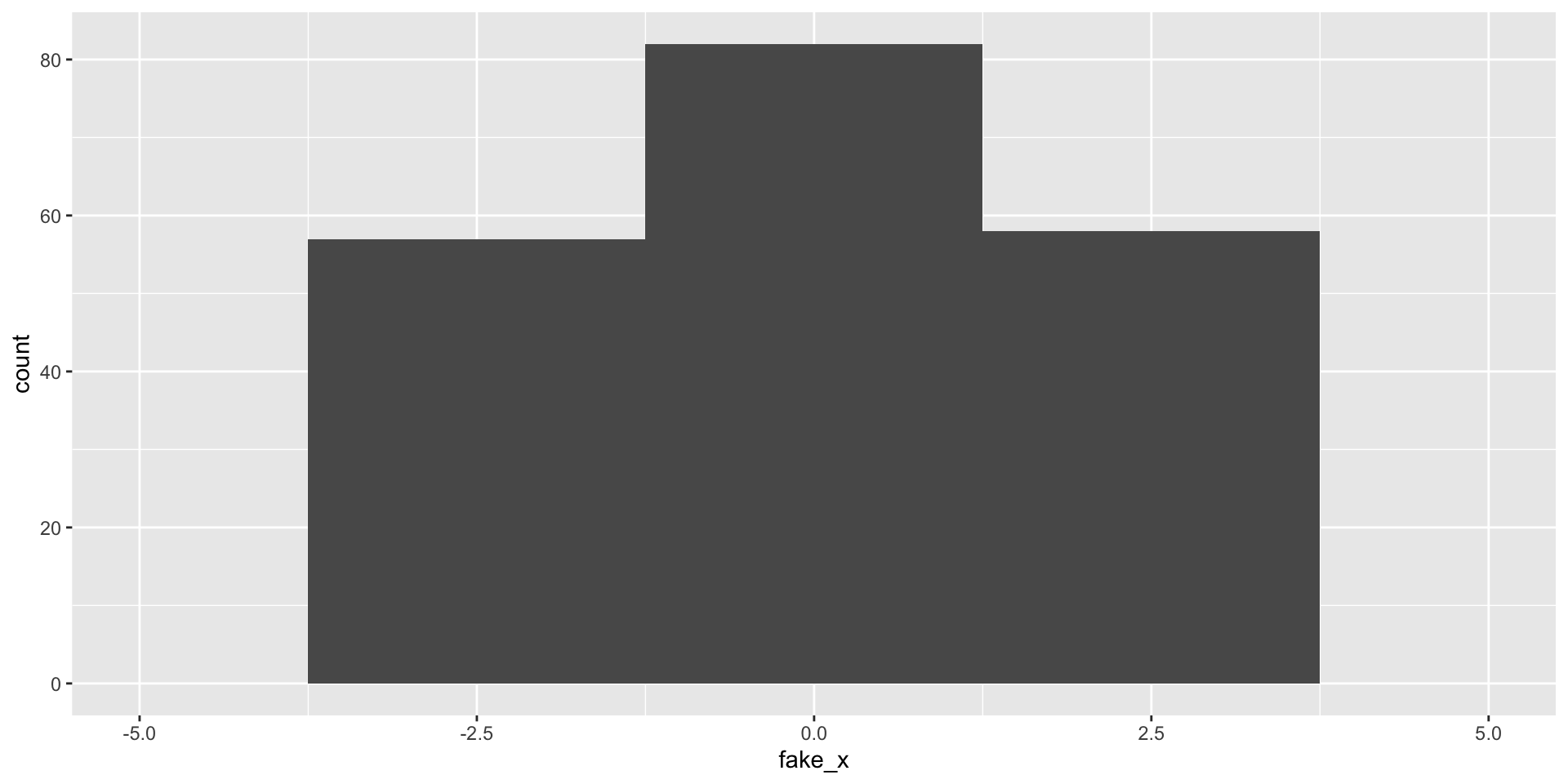
What happens as we change the number of bins?
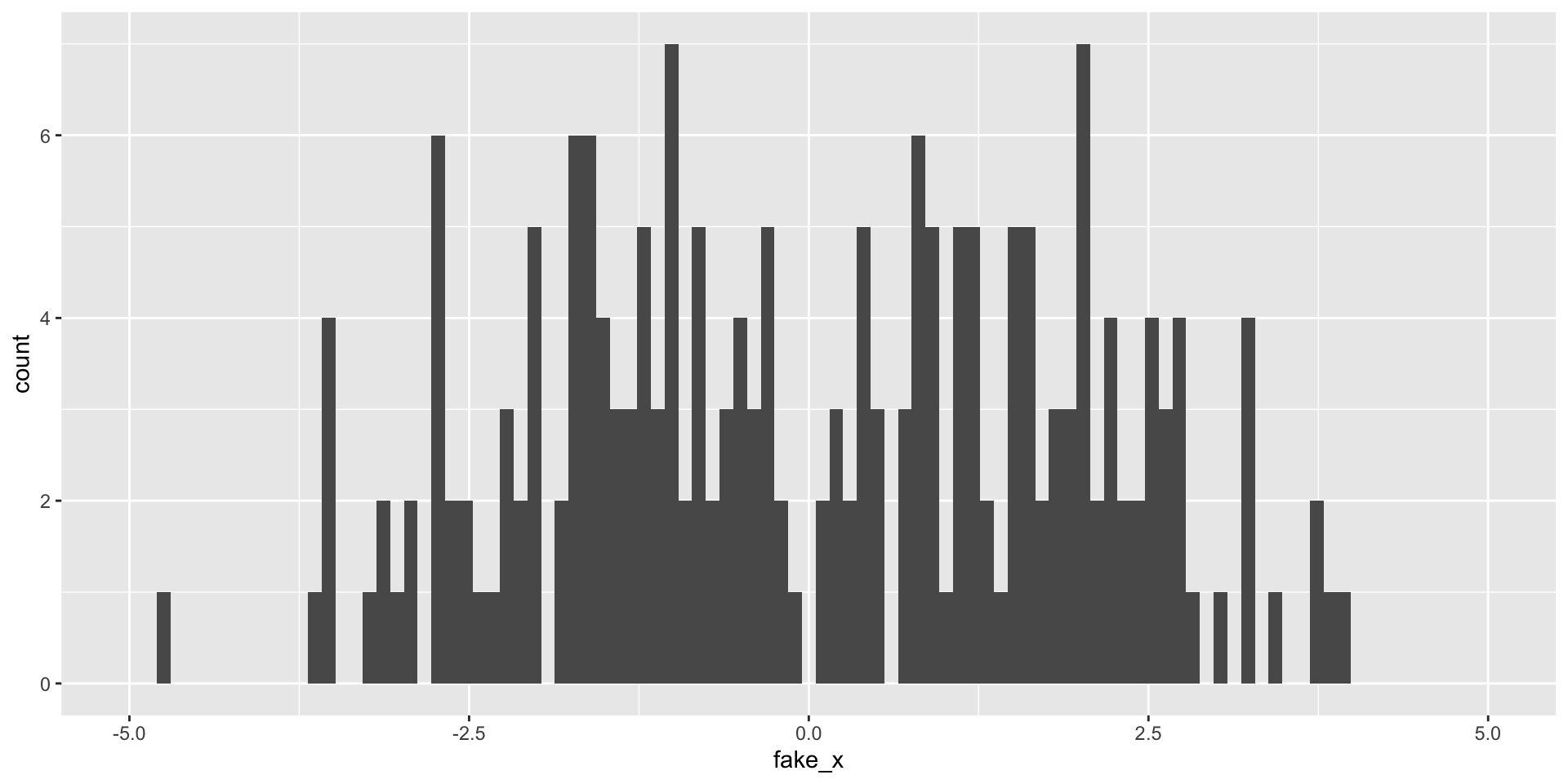
Variability of graphs - 30 bins
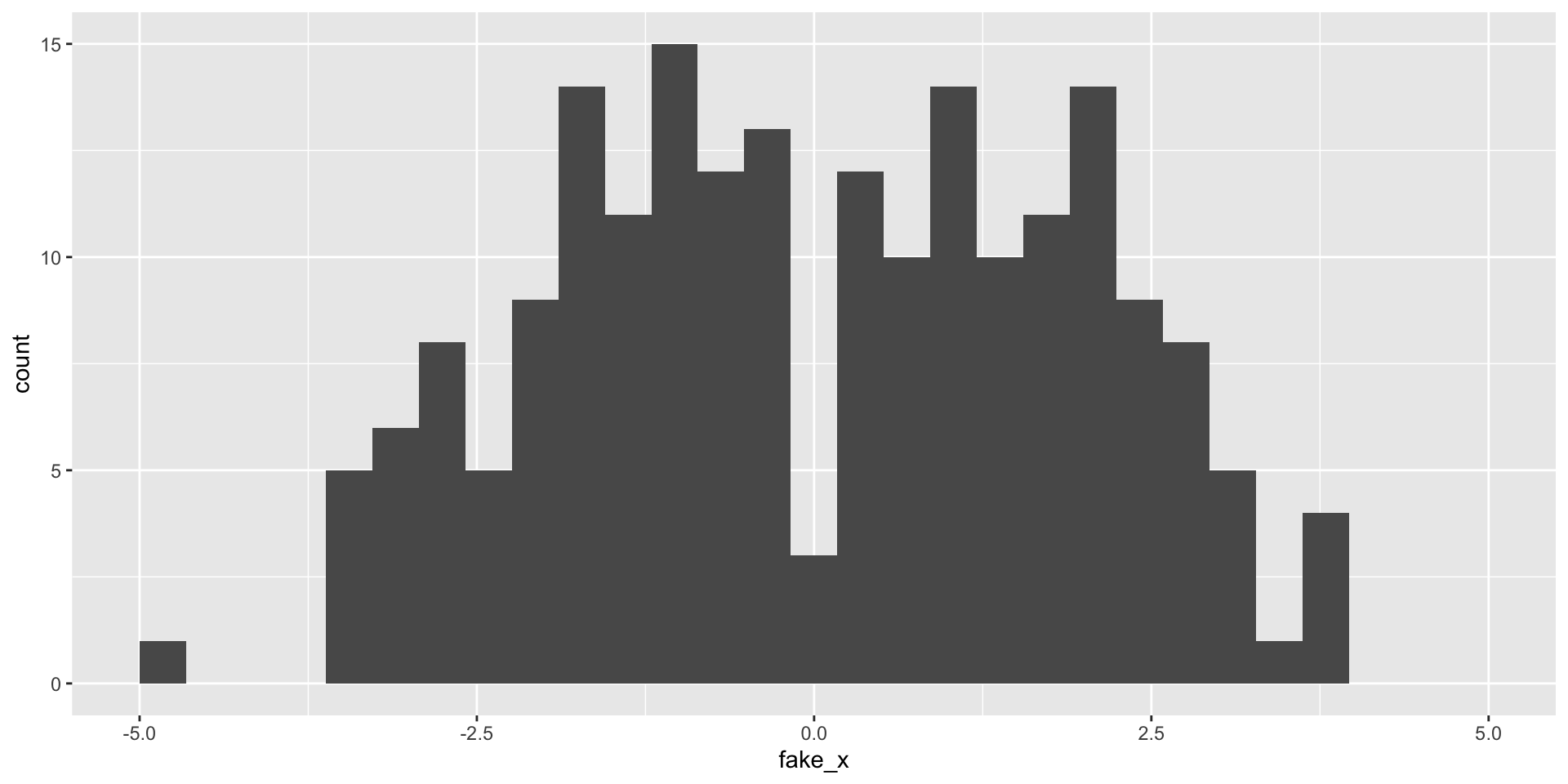
What happens with a different sample?
Variability of graphs - 15 bins
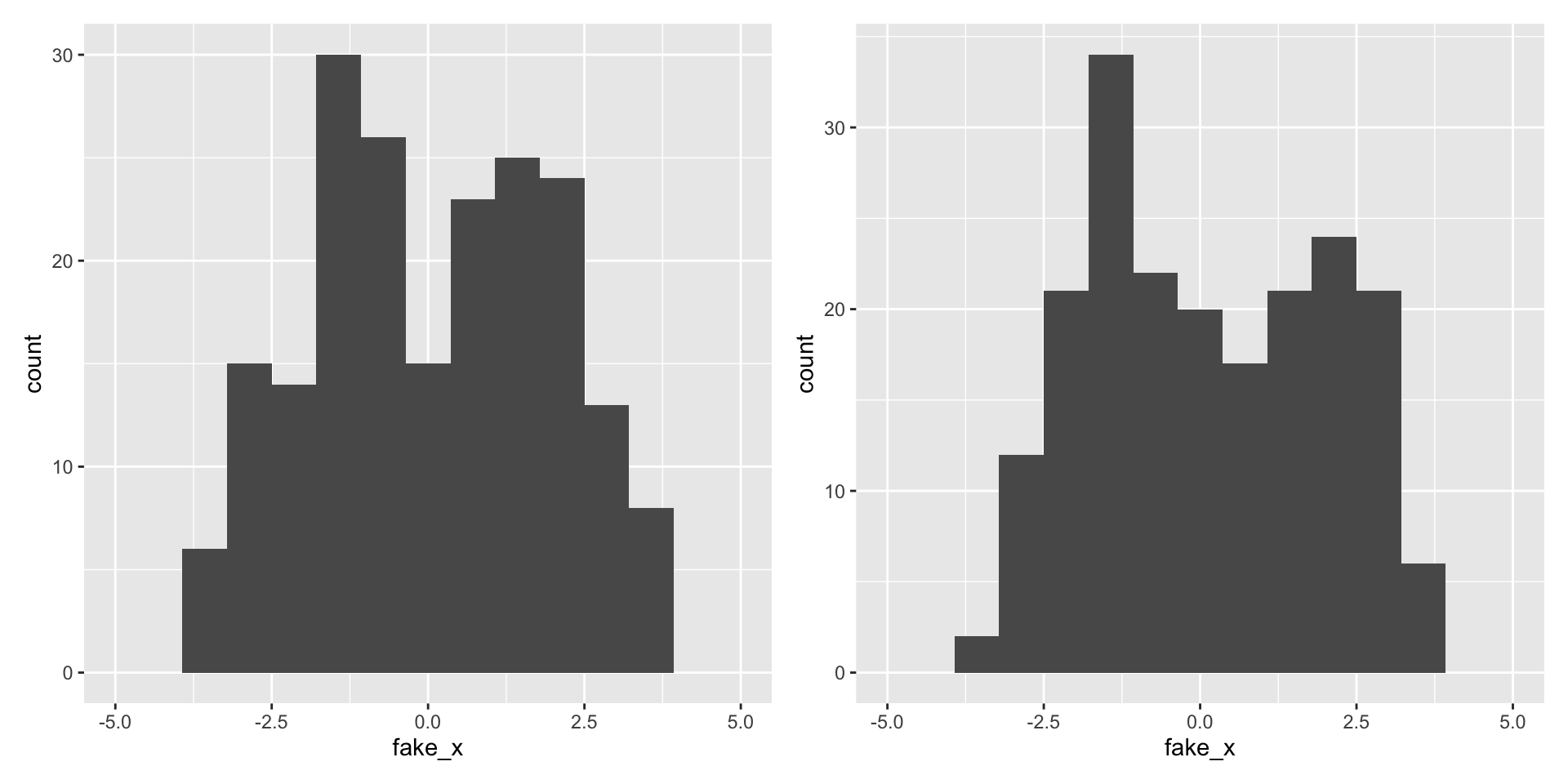
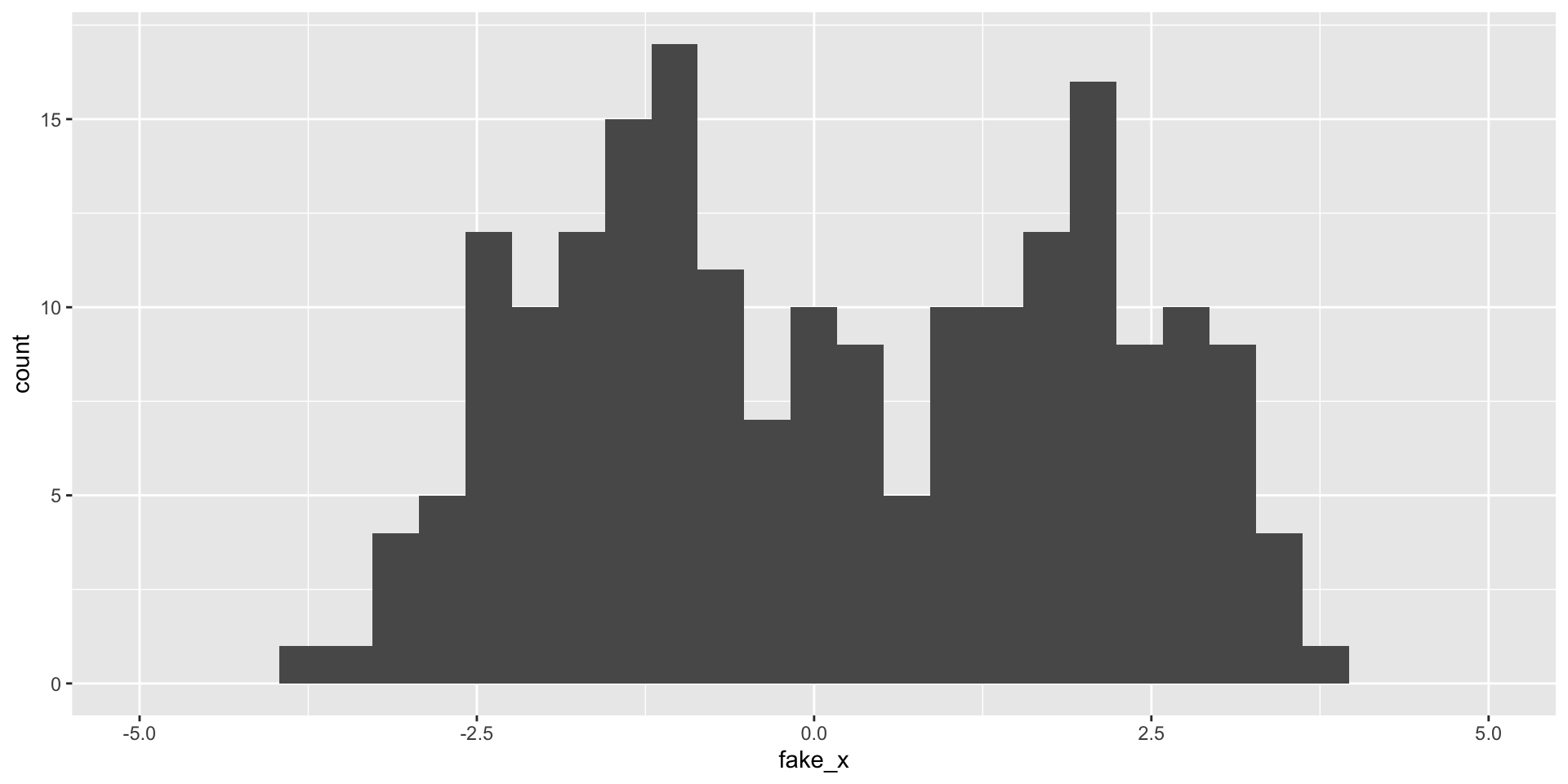
Variability of graphs - 5 bins
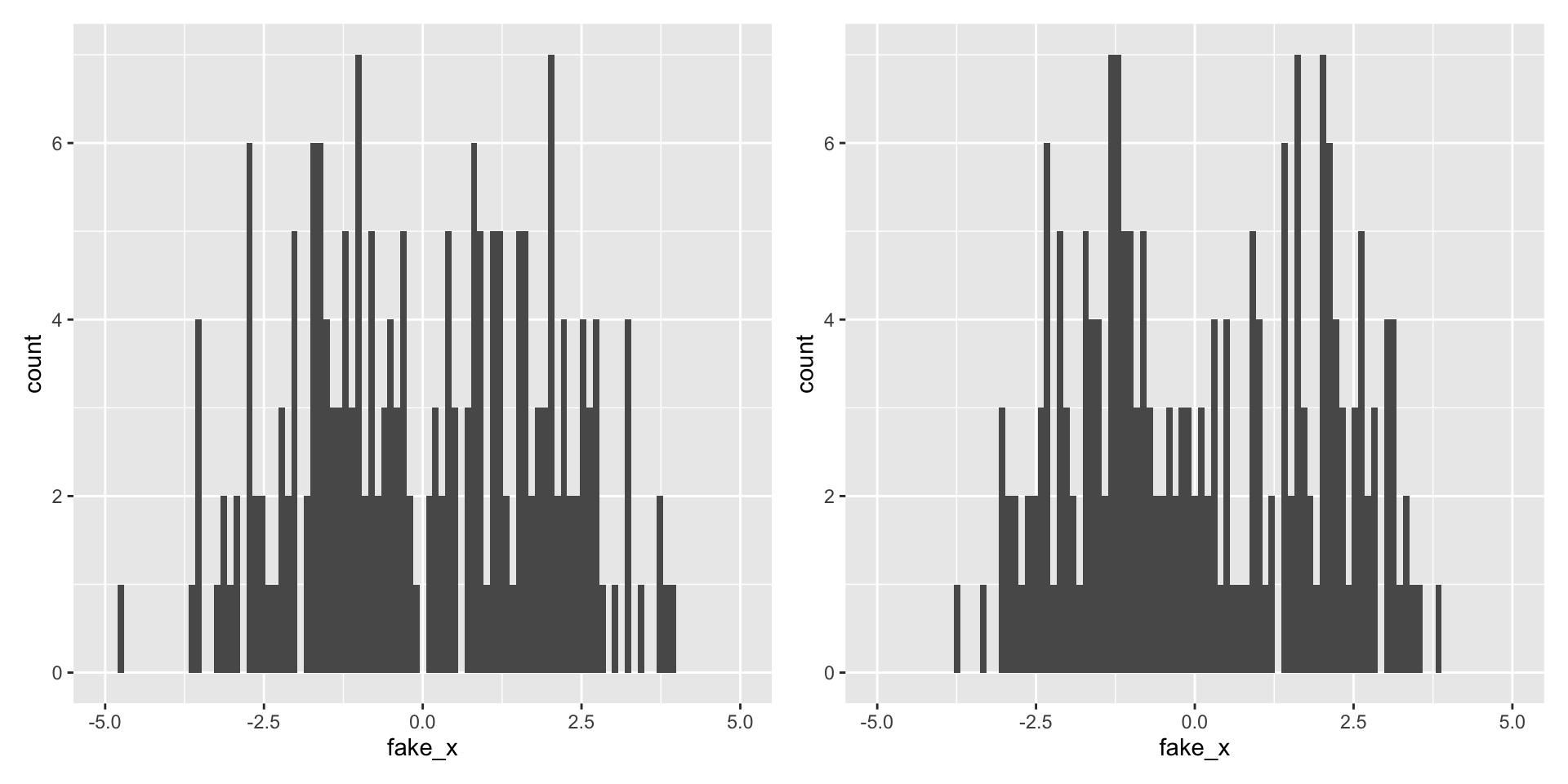
Variability of graphs - 100 bins
What do visualizations of continuous distributions display?
Probability that continuous variable \(X\) takes a particular value is 0
e.g., \(P\) (flipper_length_mm \(= 200\)) \(= 0\), why?
Instead we use the probability density function (PDF) to provide a relative likelihood
For continuous variables we can use the cumulative distribution function (CDF),
\[ F(x) = P(X \leq x) \]
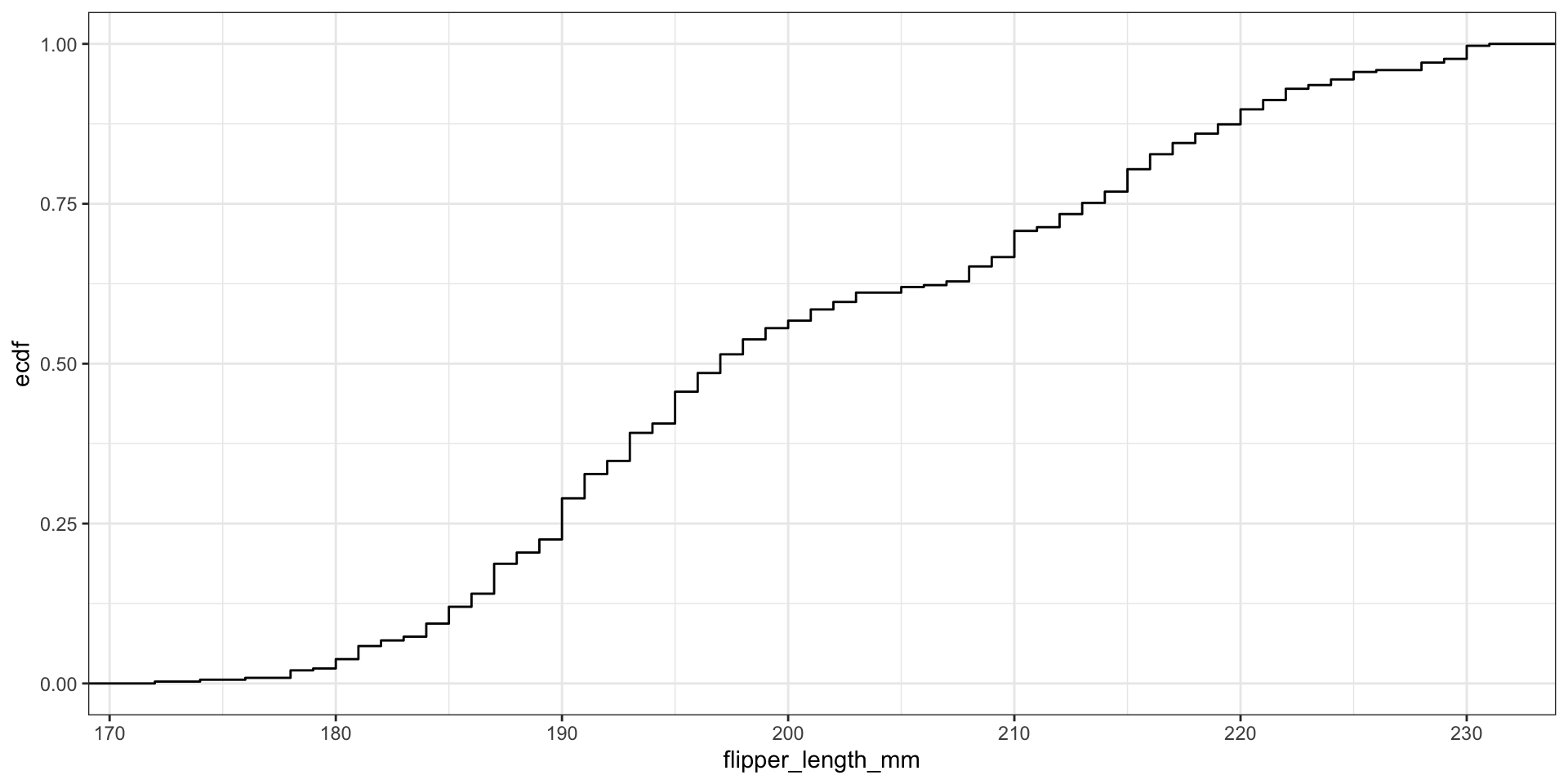
For \(n\) observations we can easily compute the Empirical CDF (ECDF):
\[\hat{F}_n(x) = \frac{\text{# obs. with variable} \leq x}{n} = \frac{1}{n} \sum_{i=1}^{n}1(x_i \leq x)\]
- where \(1()\) is the indicator function, i.e.
ifelse(x_i <= x, 1, 0)
Display full distribution with ECDF plot
What about comparing to theoretical distributions?

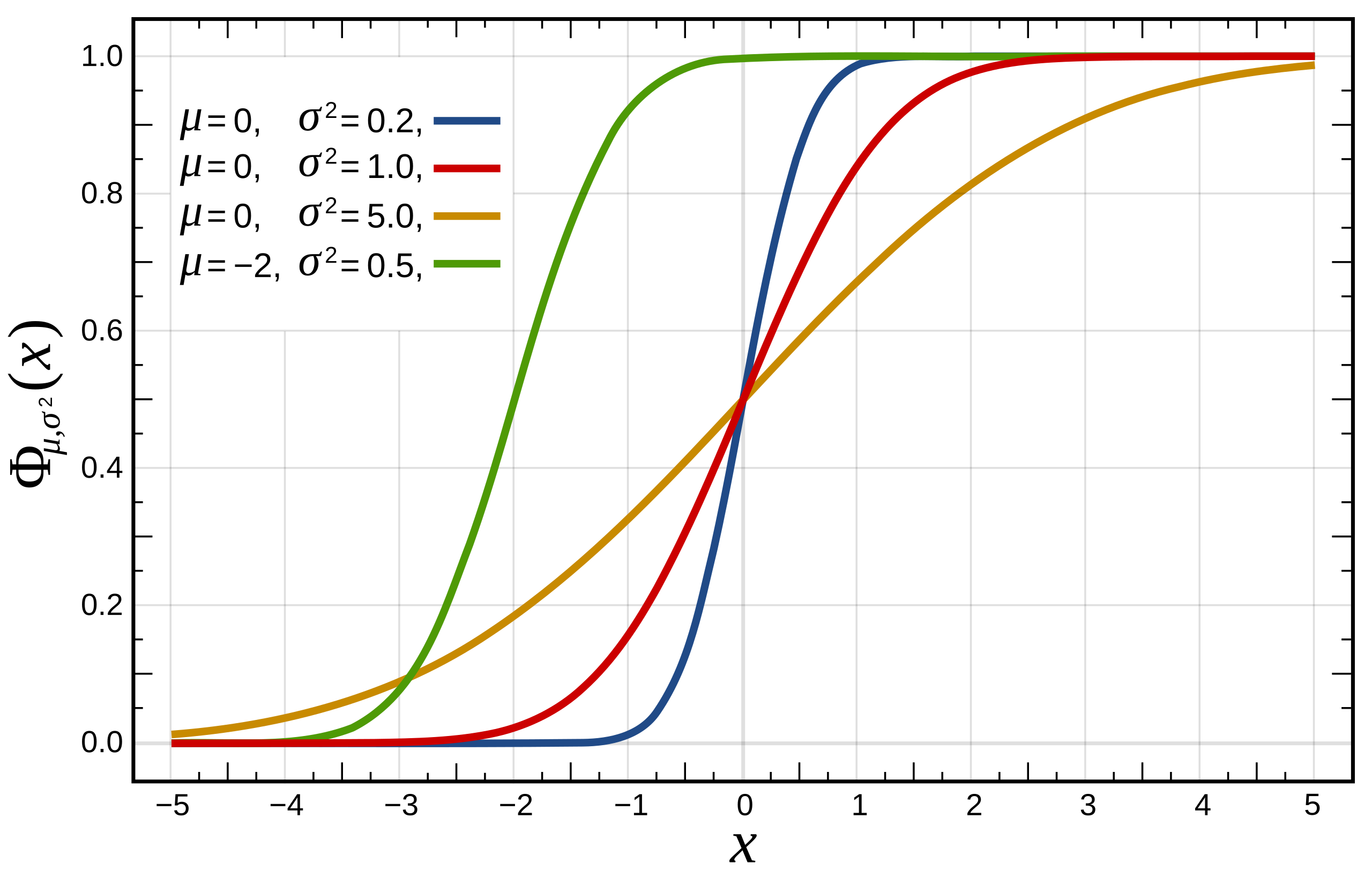
One-Sample Kolmogorov-Smirnov Test
We compare the ECDF \(\hat{F}(x)\) to a theoretical distribution’s CDF \(F(x)\)
The one sample KS test statistic is: \(\text{max}_x |\hat{F}(x) - F(x)|\)

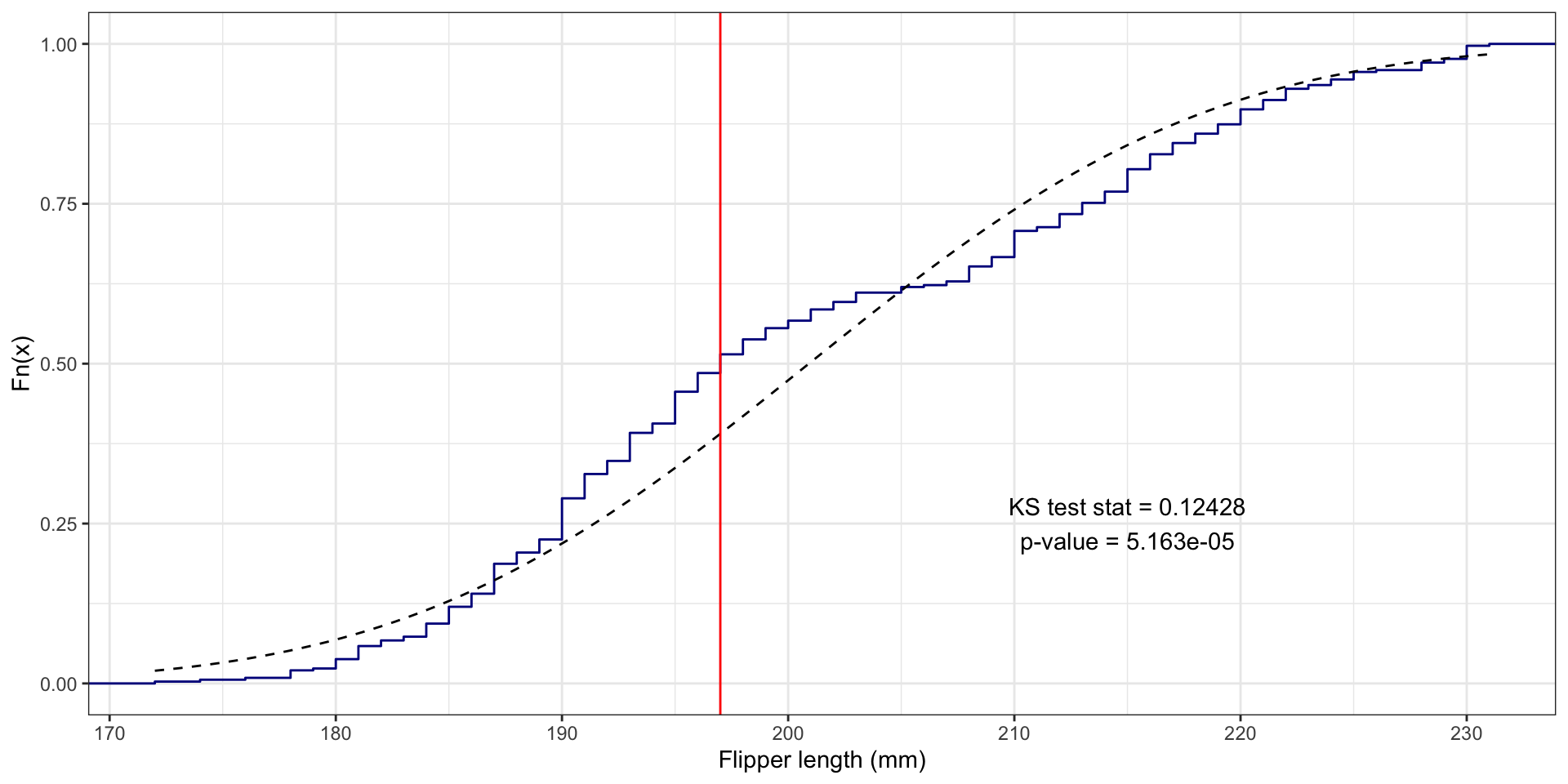
Flipper length example
What if we assume flipper_length_mm follows Normal distribution?
- i.e.,
flipper_length_mm\(\sim N(\mu, \sigma^2)\)
Need estimates for mean \(\mu\) and standard deviation \(\sigma\):
Perform one-sample KS test using ks.test():
Flipper length example
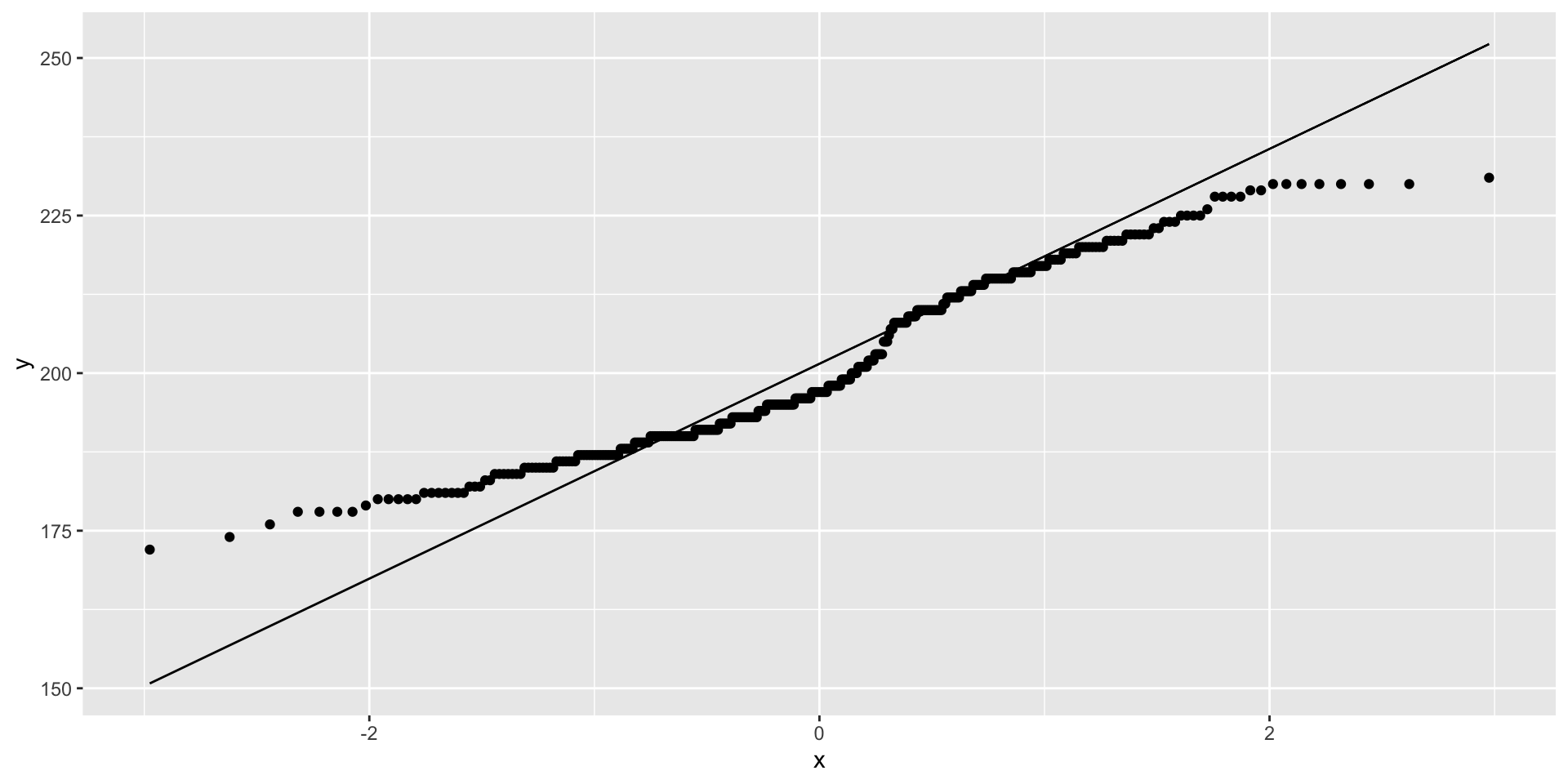
Visualize distribution comparisons using quantile-quantile (q-q) plots
What about displaying conditional distributions?
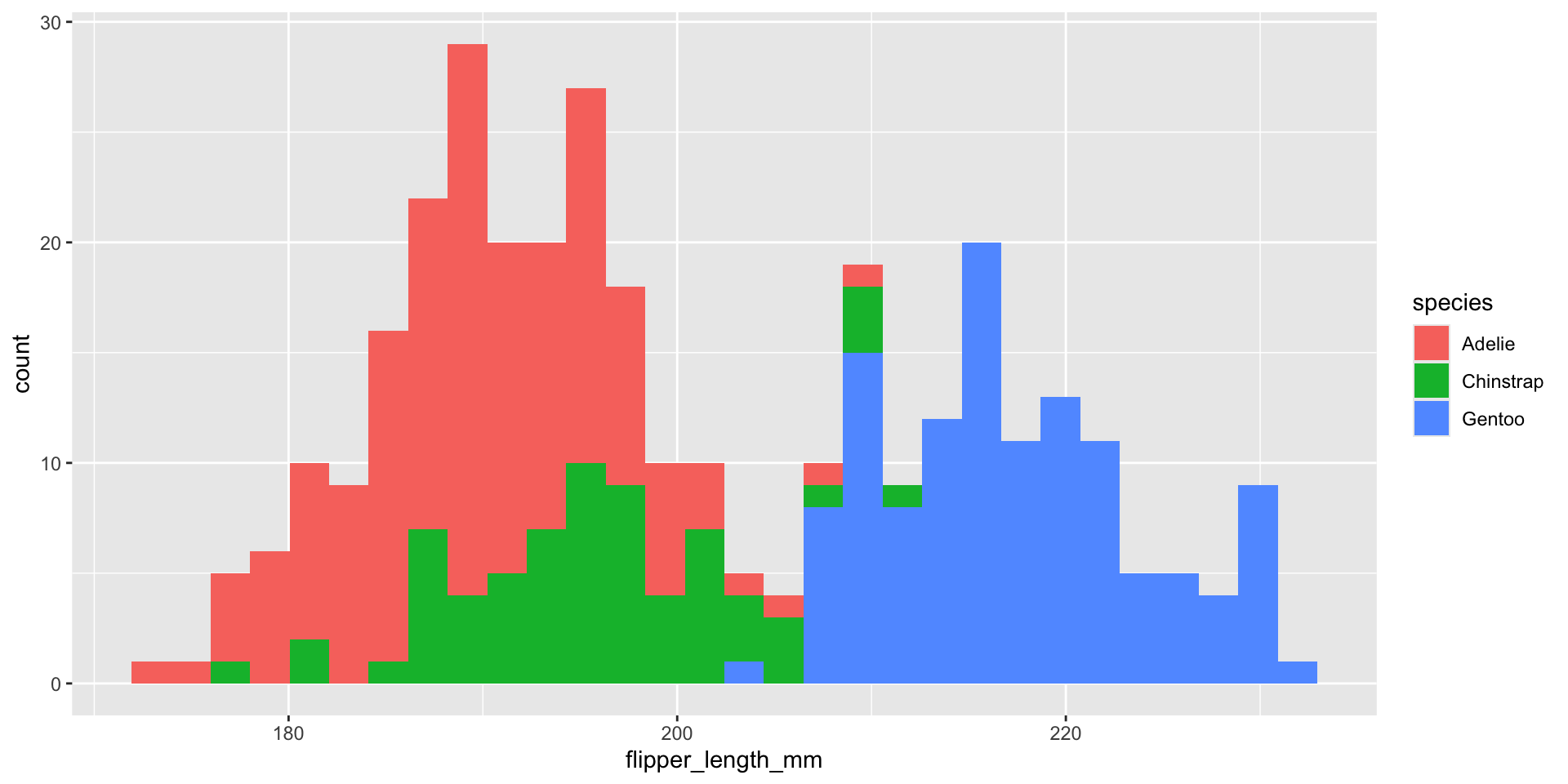
What about displaying conditional distributions?
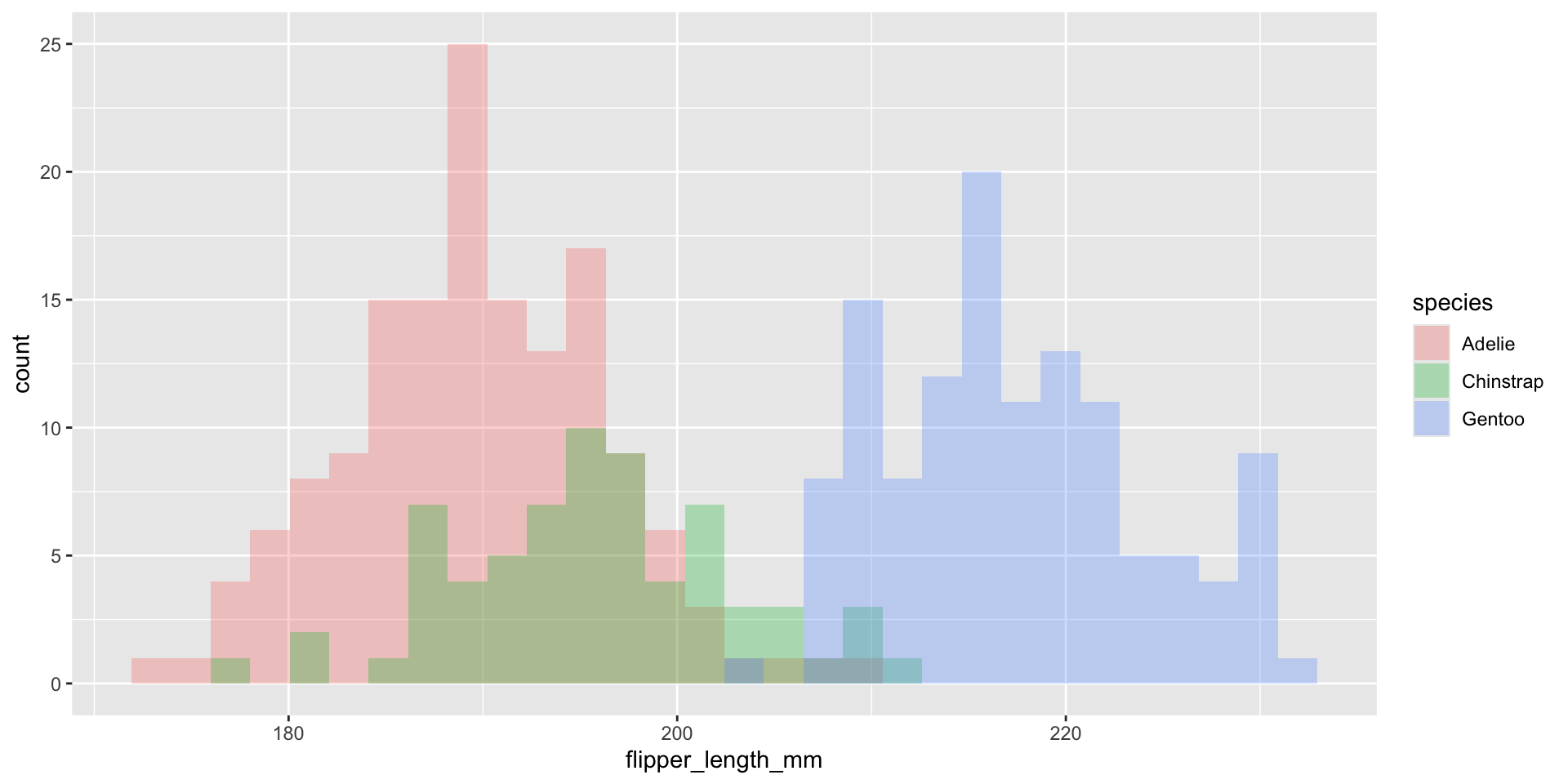
Normalize histogram frequencies with density values
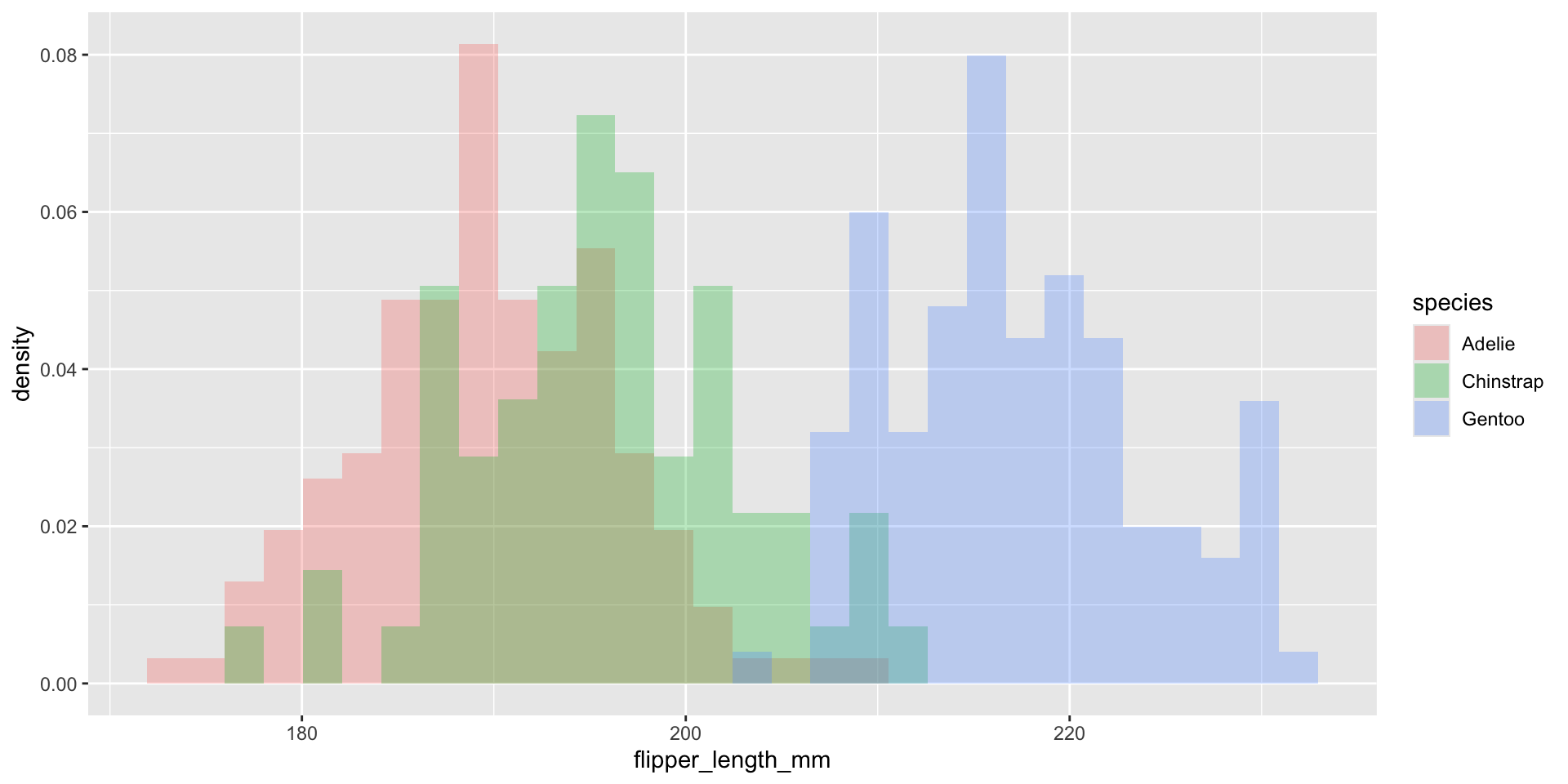
Use density curves instead for comparison
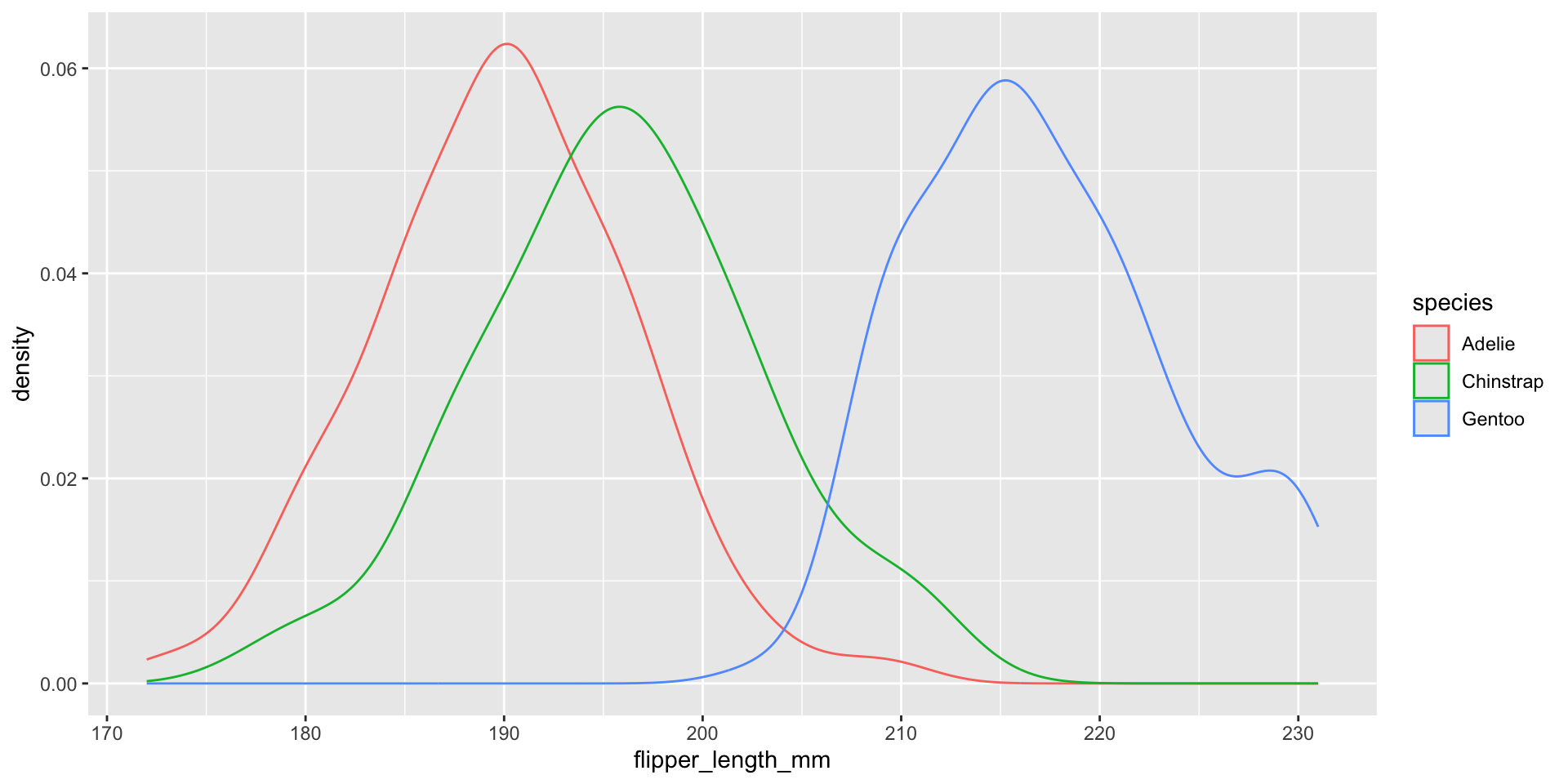
We should NOT fill the density curves
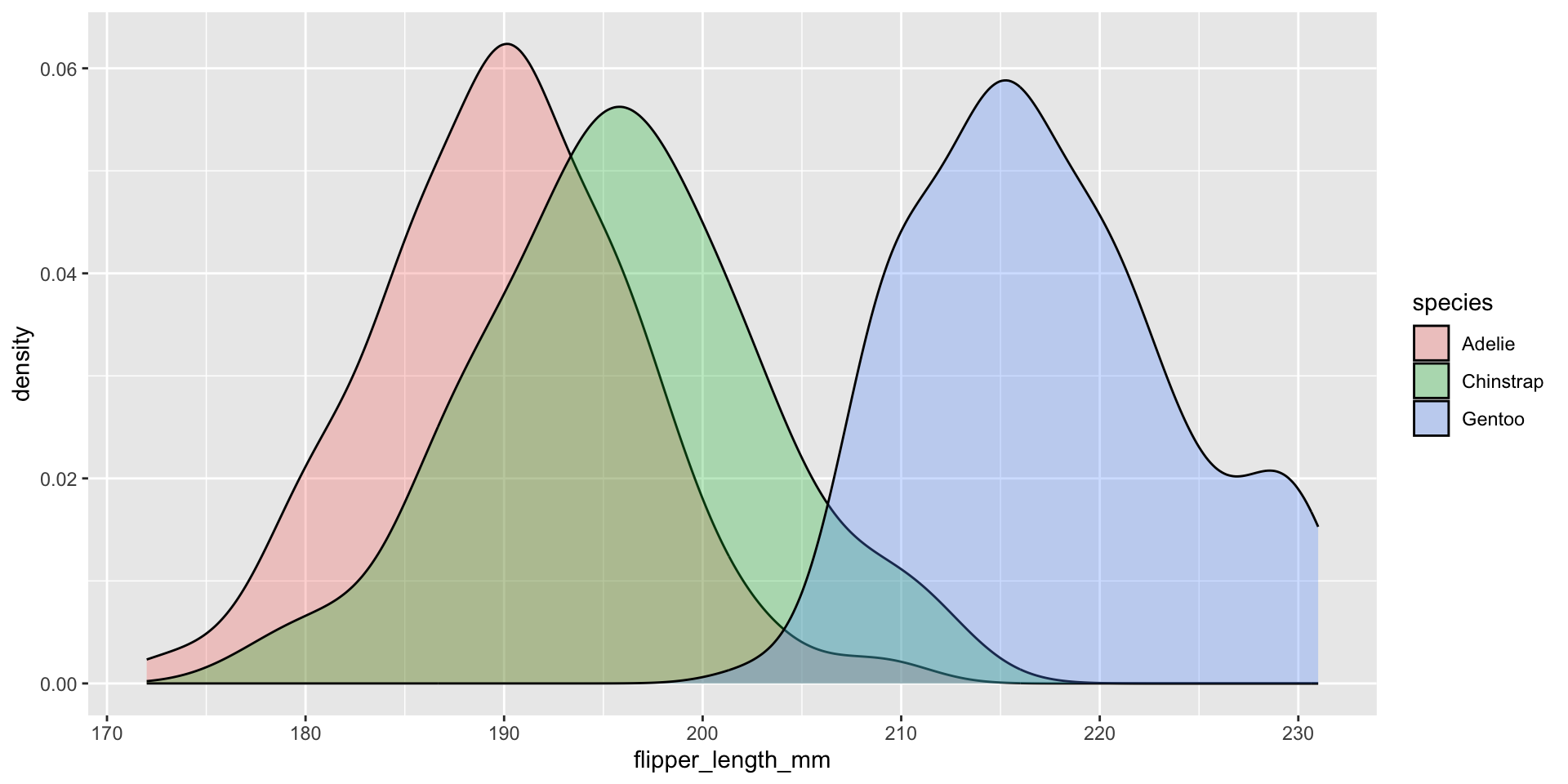
What’s the relationship between these two figures?
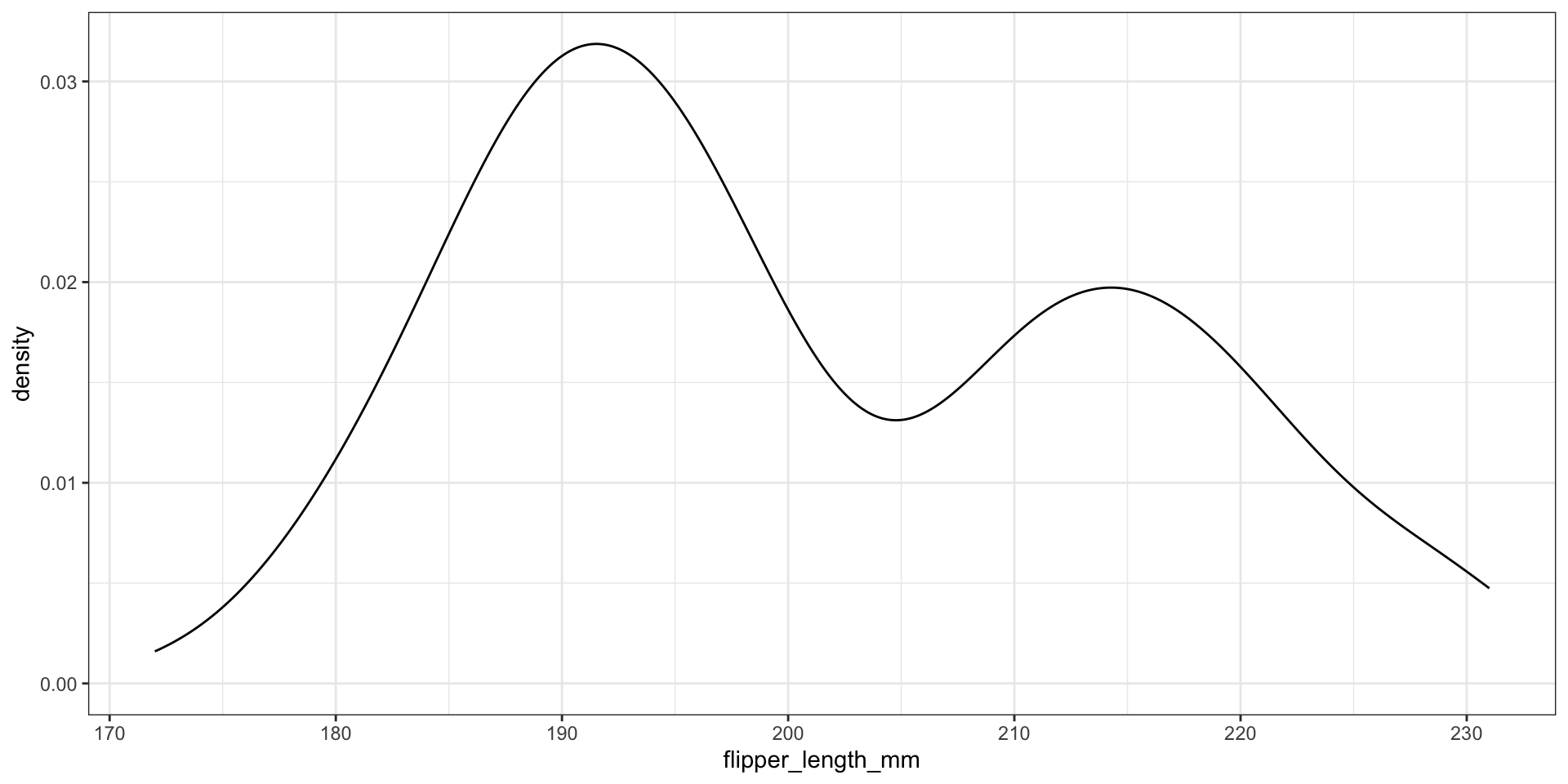
Kernel density estimation
Goal: estimate the PDF \(f(x)\) for all possible values (assuming it is continuous / smooth)
\[ \text{Kernel density estimate: } \hat{f}(x) = \frac{1}{n} \sum_{i=1}^n \frac{1}{h} K_h(x - x_i) \]
- \(n =\) sample size, \(x =\) new point to estimate \(f(x)\) (does NOT have to be in dataset!)
\(h =\) bandwidth, analogous to histogram bin width, ensures \(\hat{f}(x)\) integrates to 1
\(x_i =\) \(i\)th observation in dataset
- \(K_h(x - x_i)\) is the Kernel function, creates weight given distance of \(i\)th observation from new point
as \(|x - x_i| \rightarrow \infty\) then \(K_h(x - x_i) \rightarrow 0\), i.e. further apart \(i\)th row is from \(x\), smaller the weight
as bandwidth \(h \uparrow\) weights are more evenly spread out (as \(h \downarrow\) more concentrated around \(x\))
typically use Gaussian / Normal kernel: \(\propto e^{-(x - x_i)^2 / 2h^2}\)
\(K_h(x - x_i)\) is large when \(x_i\) is close to \(x\)
Wikipedia example

We display kernel density estimates with geom_density()
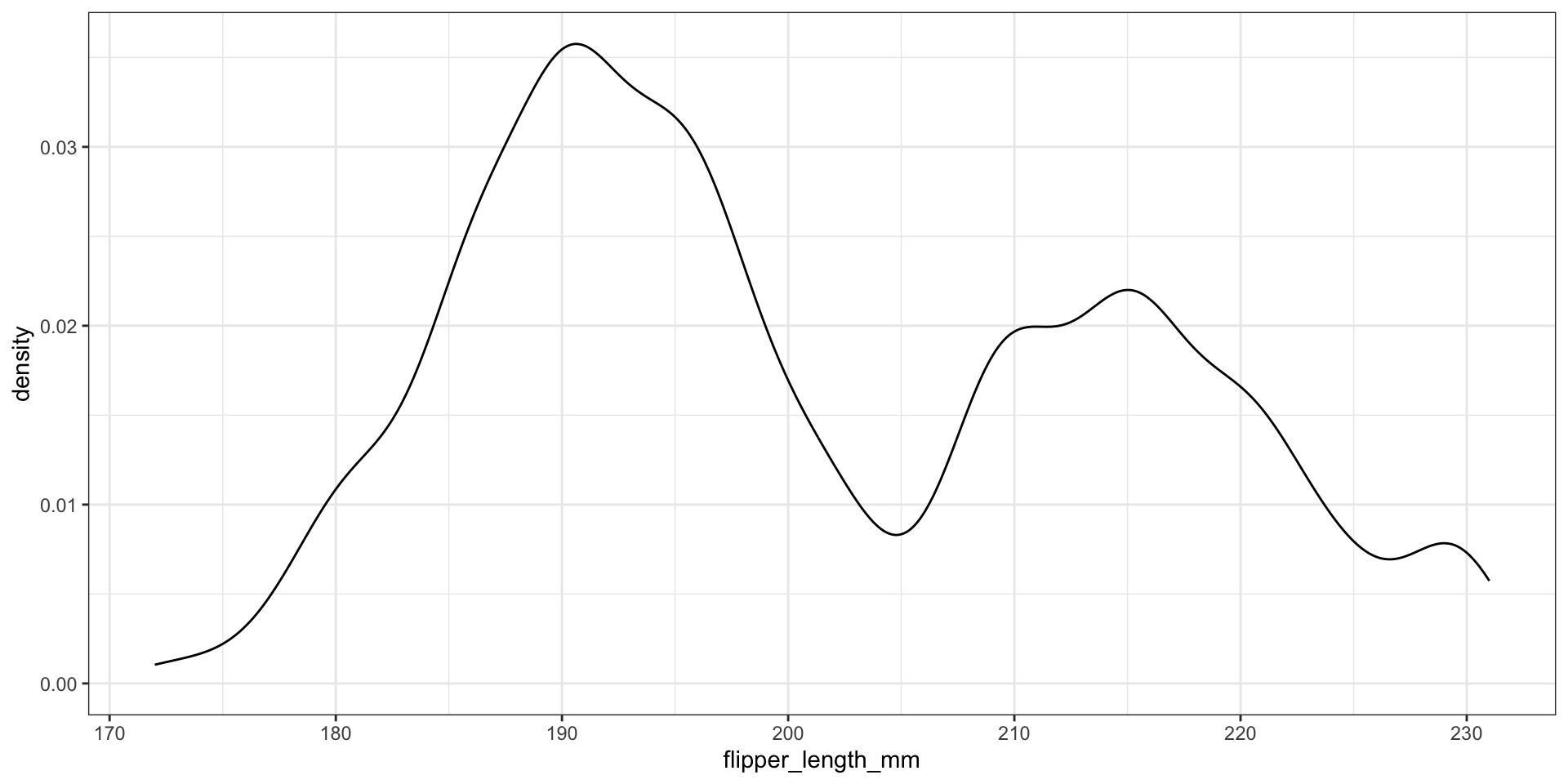
Choice of kernel?

What about the bandwidth?
Use Gaussian reference rule (rule-of-thumb) \(\approx 1.06 \cdot \sigma \cdot n^{-1/5}\), where \(\sigma\) is the observed standard deviation
Modify the bandwidth using the adjust argument - value to multiply default bandwidth by
What about the bandwidth?
Use Gaussian reference rule (rule-of-thumb) \(\approx 1.06 \cdot \sigma \cdot n^{-1/5}\), where \(\sigma\) is the observed standard deviation
Modify the bandwidth using the adjust argument - value to multiply default bandwidth by
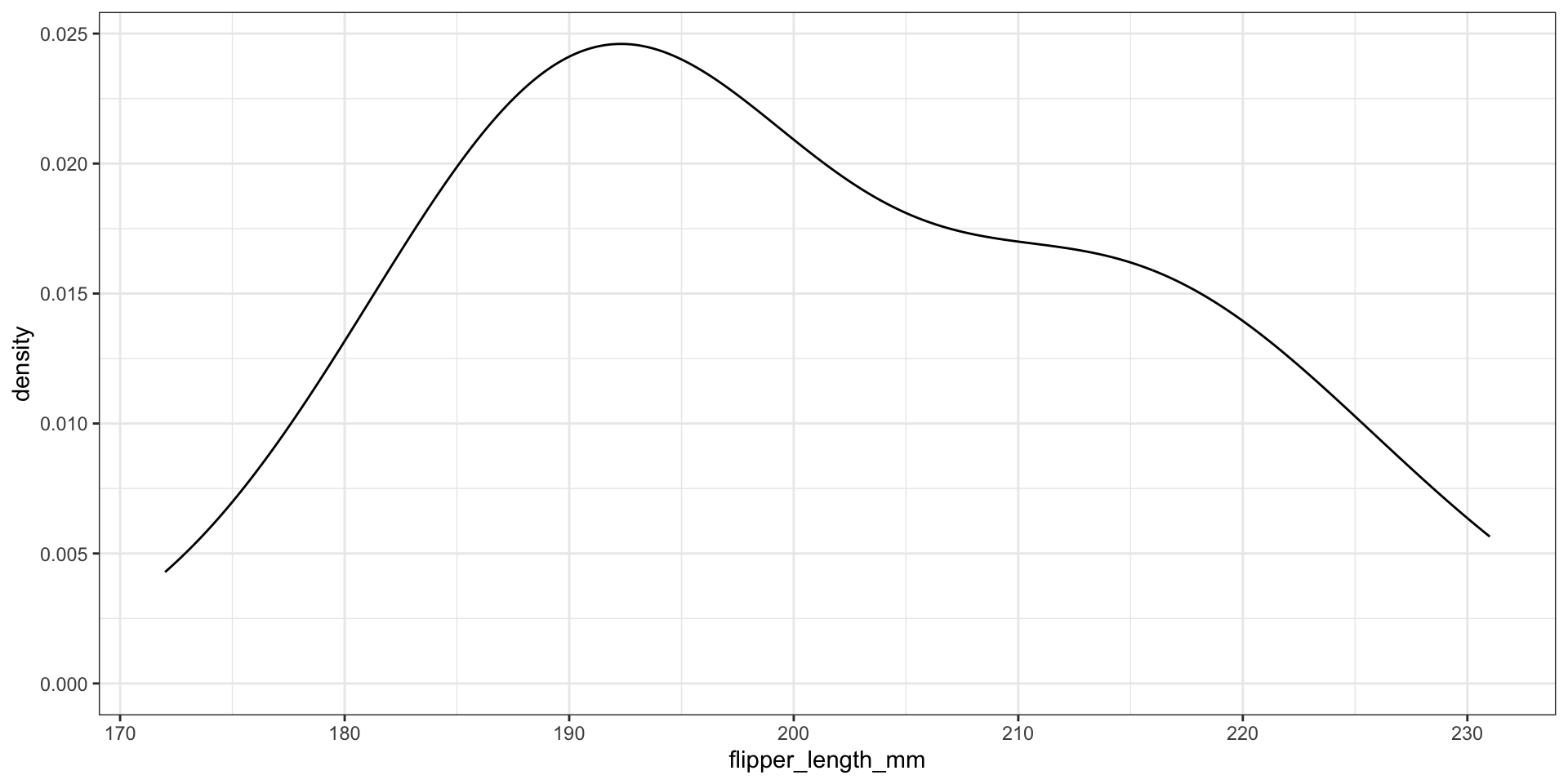
CAUTION: dealing with bounded data…
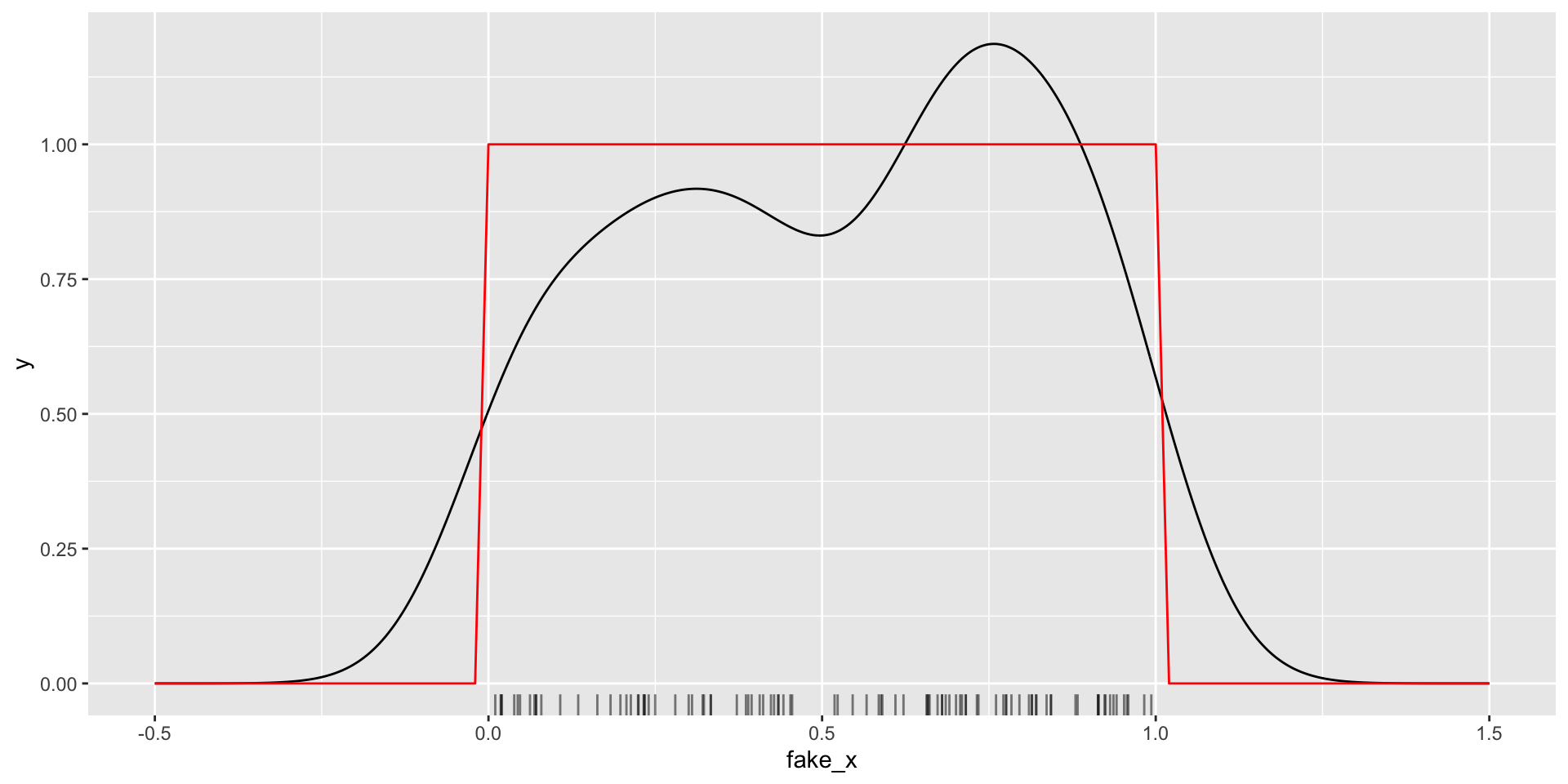
Visualizing conditional distributions with violin plots
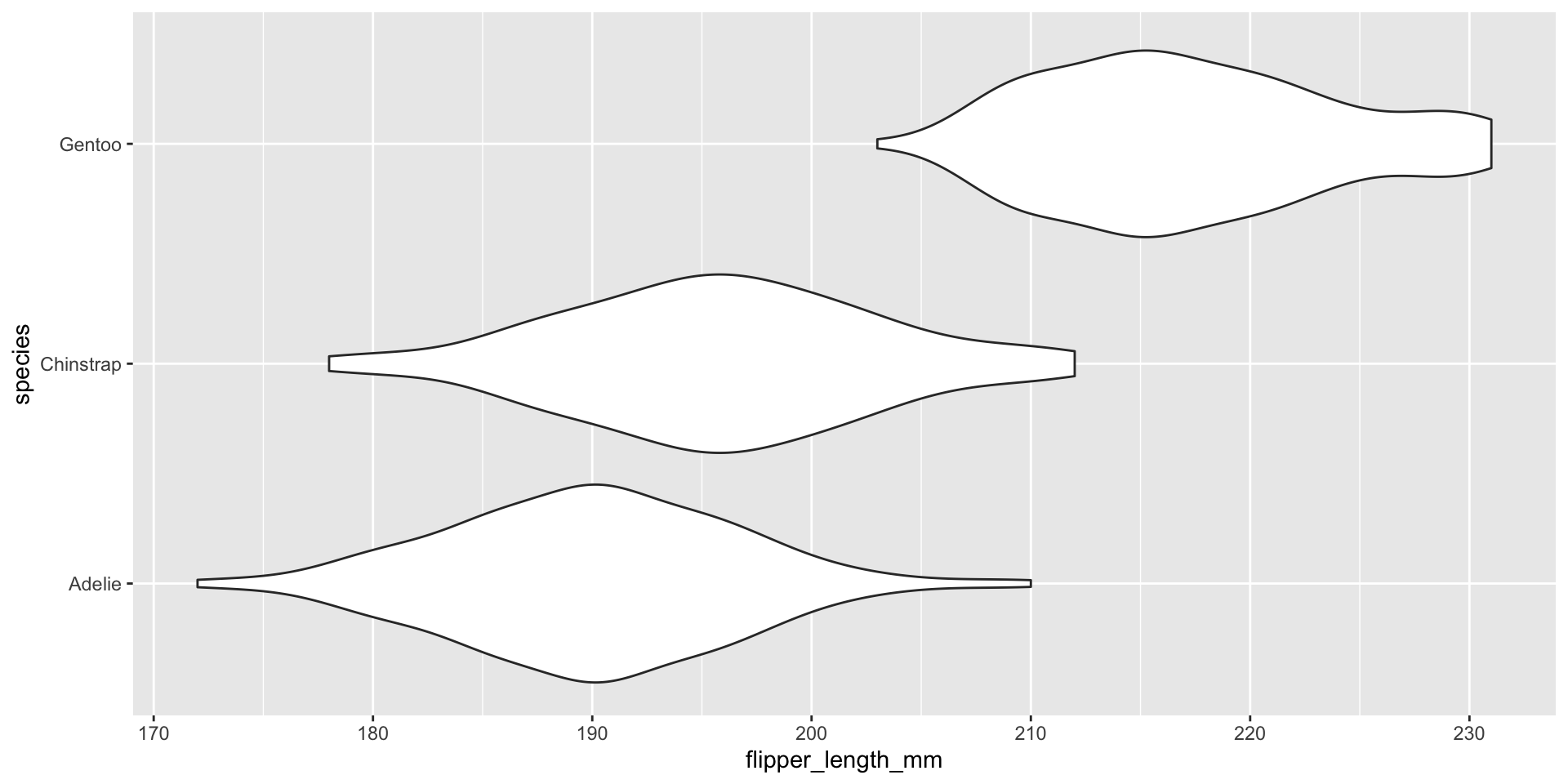
Visualizing conditional distributions with violin plots
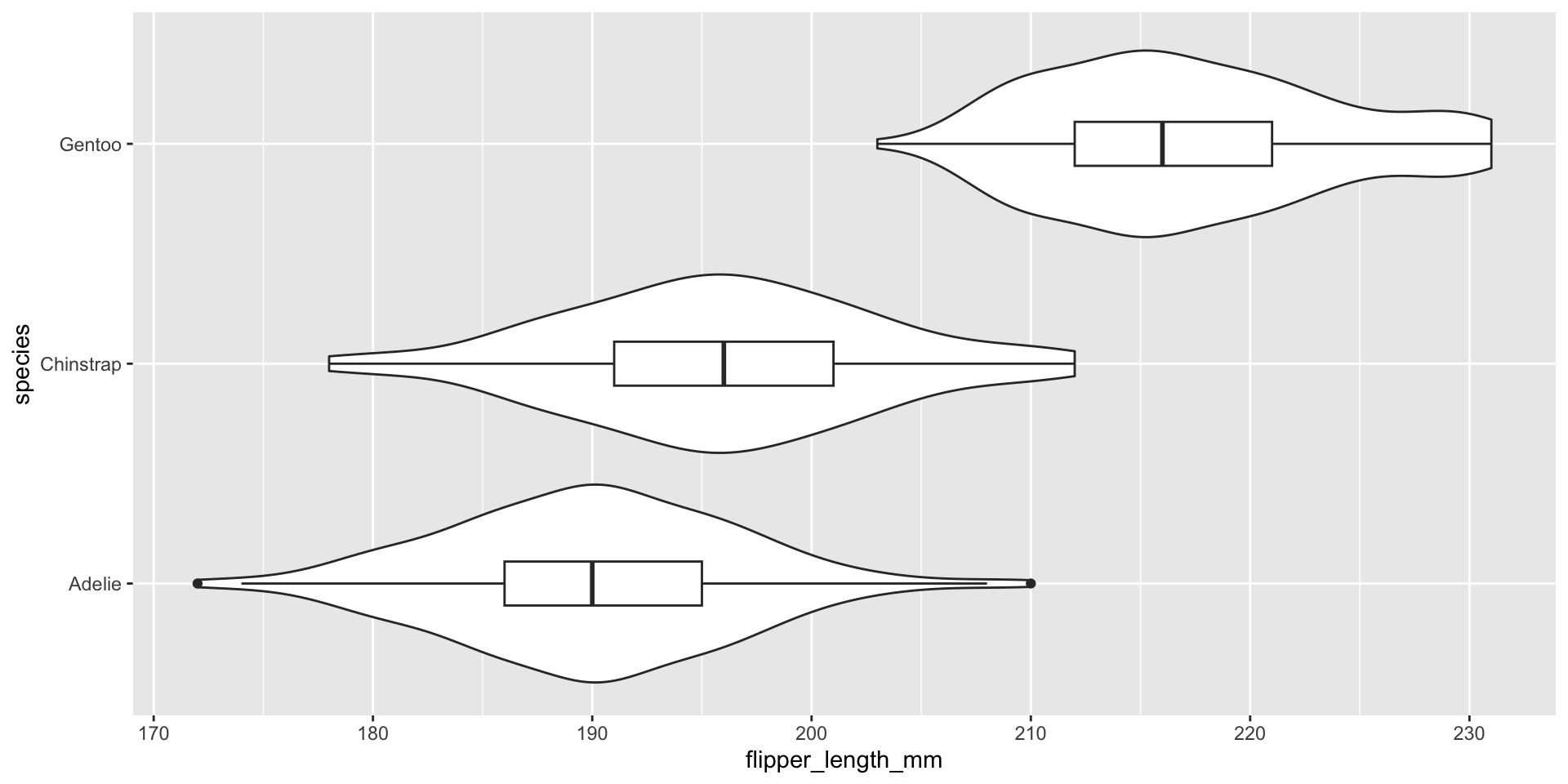
Visualizing conditional distributions with ggridges package
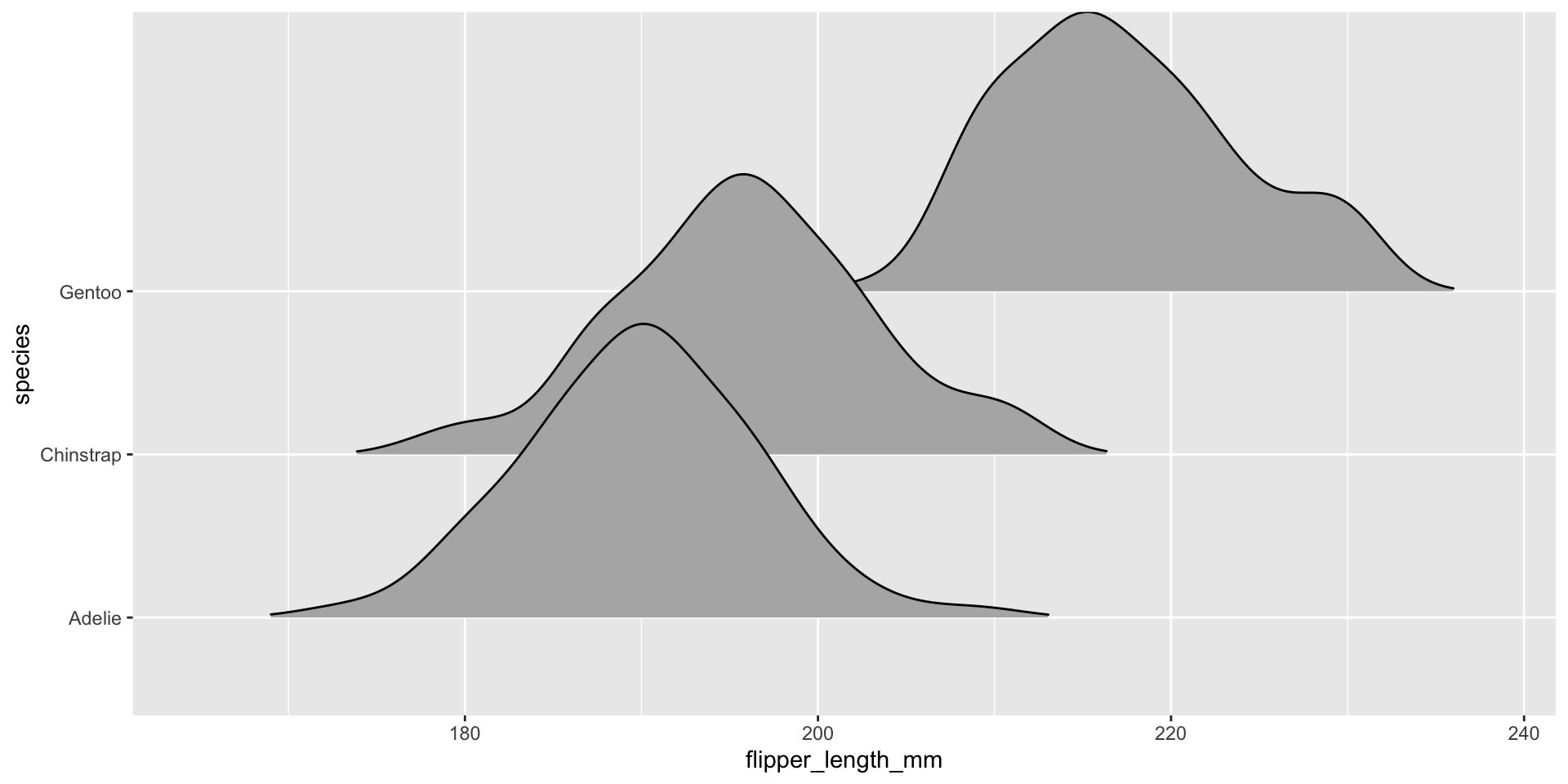
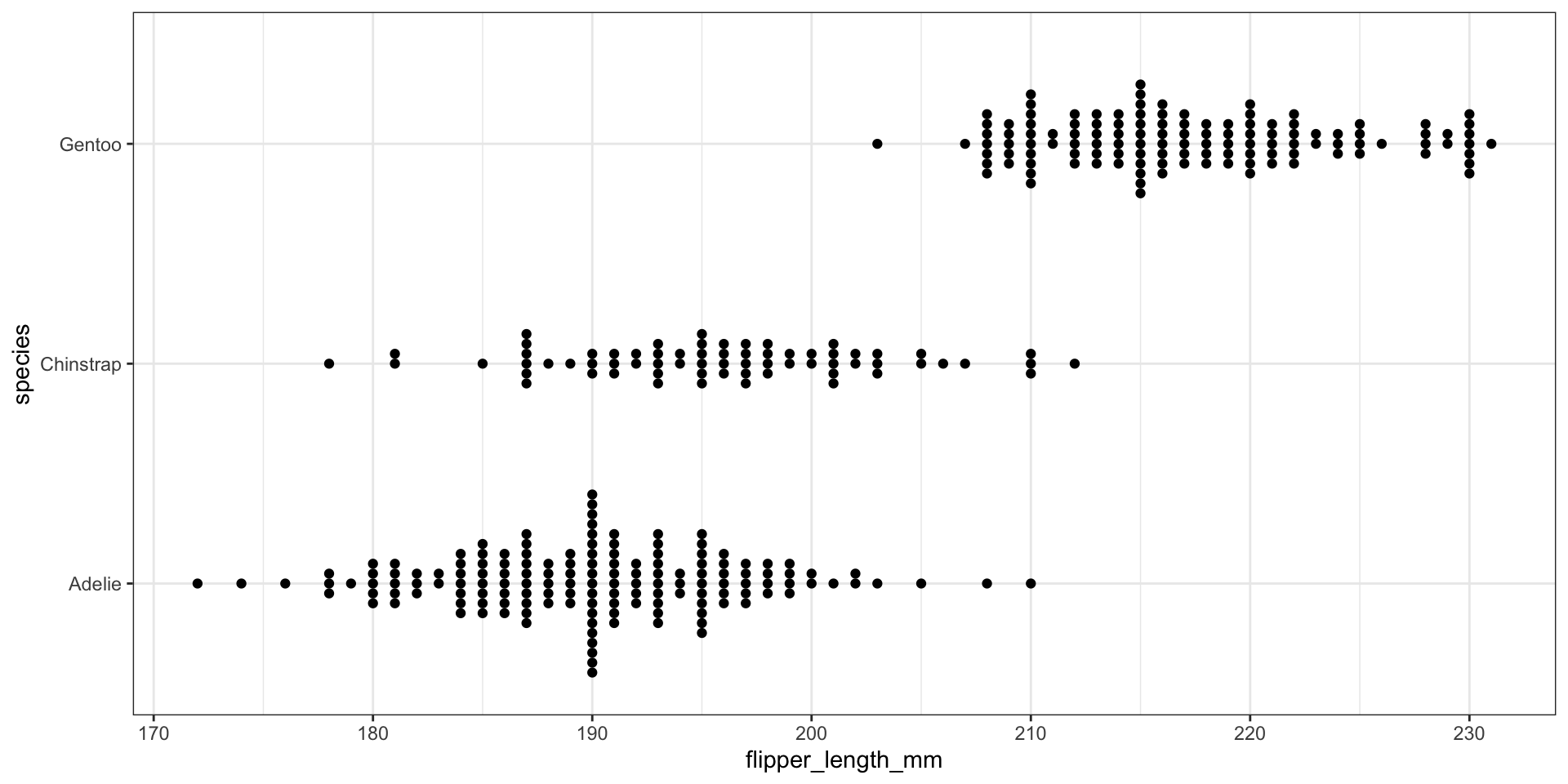
Visualizing conditional distributions with ggbeeswarm package
Recap and next steps
Discussed impact of bins on histograms
Covered ECDFs and connection to KS-tests
Walked through density estimation
Discussed ways of visualizing conditional distributions
HW2 is due Wednesday Sept 11th!
HW3 is posted and due next Wednesday Sept 18th
Next time: 2D quantitative data
Recommended reading:
CW Chapter 7 Visualizing distributions: Histograms and density plots, CW Chapter 8 Visualizing distributions: Empirical cumulative distribution functions and q-q plots
BONUS: Visualizing the KS test statistic
# First create the ECDF function for the variable:
fl_ecdf <- ecdf(penguins$flipper_length_mm)
# Compute the absolute value of the differences between the ECDF for the values
# and the theoretical values with assumed Normal distribution:
abs_ecdf_diffs <- abs(fl_ecdf(penguins$flipper_length_mm) - pnorm(penguins$flipper_length_mm,
mean = flipper_length_mean, sd = flipper_length_sd))
# Now find where the maximum difference is:
max_abs_ecdf_diff_i <- which.max(abs_ecdf_diffs)
# Get this flipper length value:
max_fl_diff_value <- penguins$flipper_length_mm[max_abs_ecdf_diff_i]
# Plot the ECDF with the theoretical Normal and KS test info:
penguins |>
ggplot(aes(x = flipper_length_mm)) +
stat_ecdf(color = "darkblue") +
# Use stat_function to draw the Normal ECDF
stat_function(fun = pnorm, args = list(mean = flipper_length_mean, sd = flipper_length_sd), color = "black", linetype = "dashed") +
# Draw KS test line:
geom_vline(xintercept = max_fl_diff_value, color = "red") +
# Add text with the test results (x and y are manually entered locations)
annotate(geom = "text", x = 215, y = .25, label = "KS test stat = 0.12428\np-value = 5.163e-05") +
labs(x = "Flipper length (mm)", y = "Fn(x)") + theme_bw()