set.seed(2013)
tsne_fit <- starbucks |>
dplyr::select(serv_size_m_l:caffeine_mg) |>
scale() |>
Rtsne(check_duplicates = FALSE)
starbucks |>
mutate(tsne1 = tsne_fit$Y[,1],
tsne2 = tsne_fit$Y[,2]) |>
ggplot(aes(x = tsne1, y = tsne2,
color = size)) +
geom_point(alpha = 0.5) +
labs(x = "t-SNE 1", y = "t-SNE 2")t-SNE + visualizing trends and time series data
2024-09-23
Reminders, previously, and today…
HW4 is due Wednesday Sept 25th
You need to email me a draft of your EDA report! (1 per group)
Walked through PCA for dimension reduction
Discussed choosing the number of PCs with scree plots
Created biplots for interpreting variable contributions to PCs
TODAY:
Introduce non-linear dimension reduction with t-SNE plots
Discuss visualizing trends
Walk through the basics of time series data
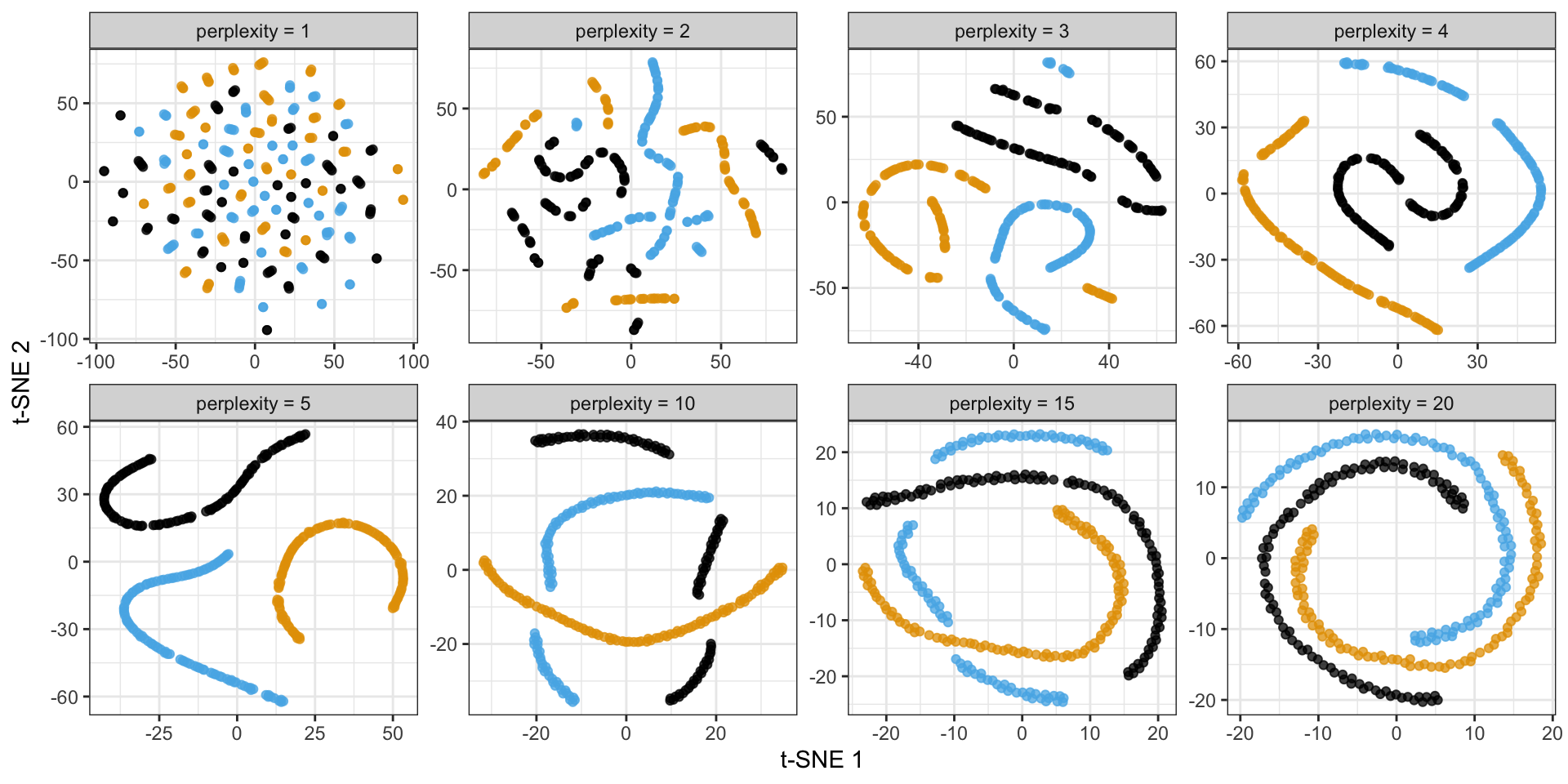
Consider the following spiral structure…
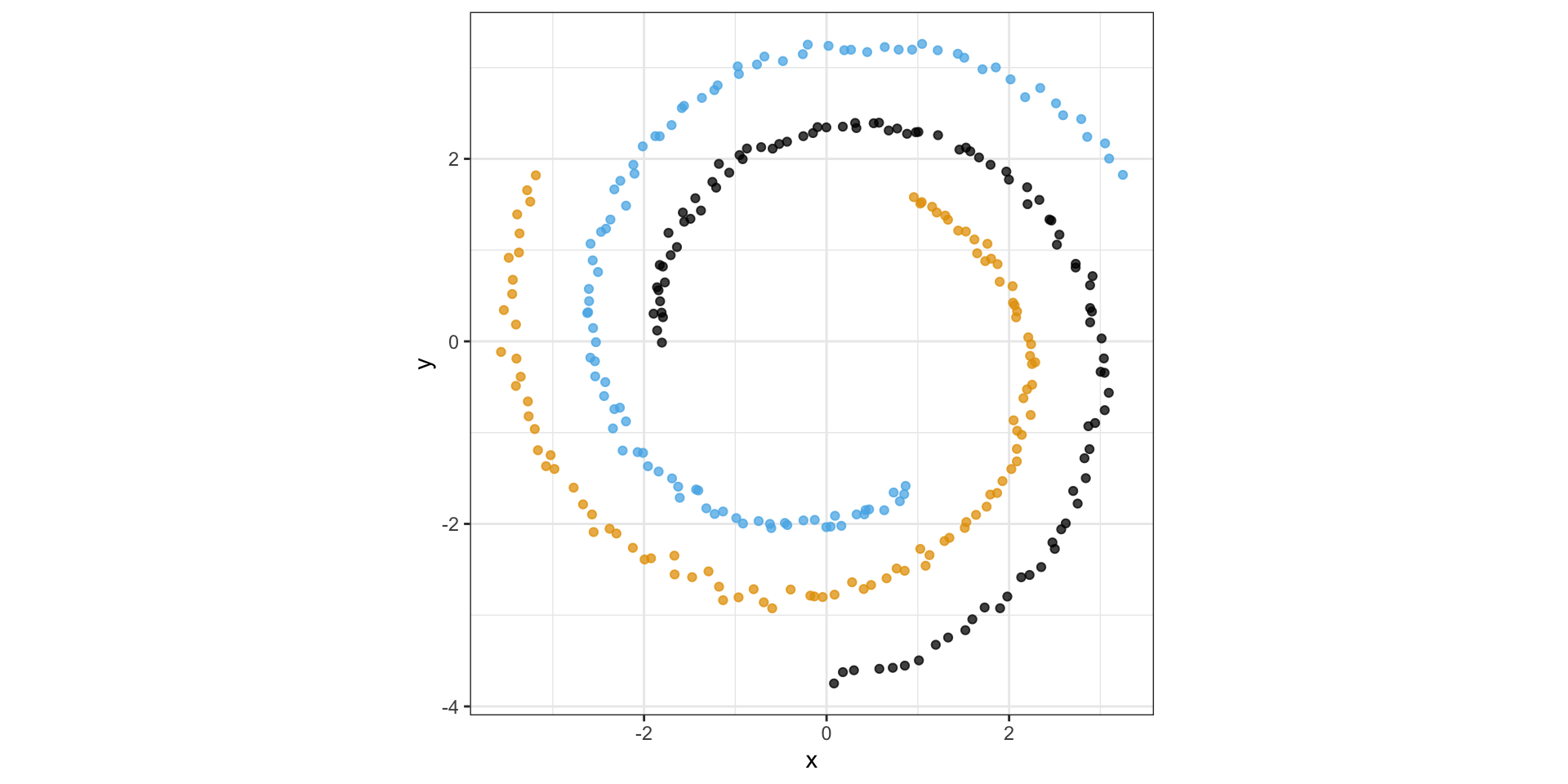
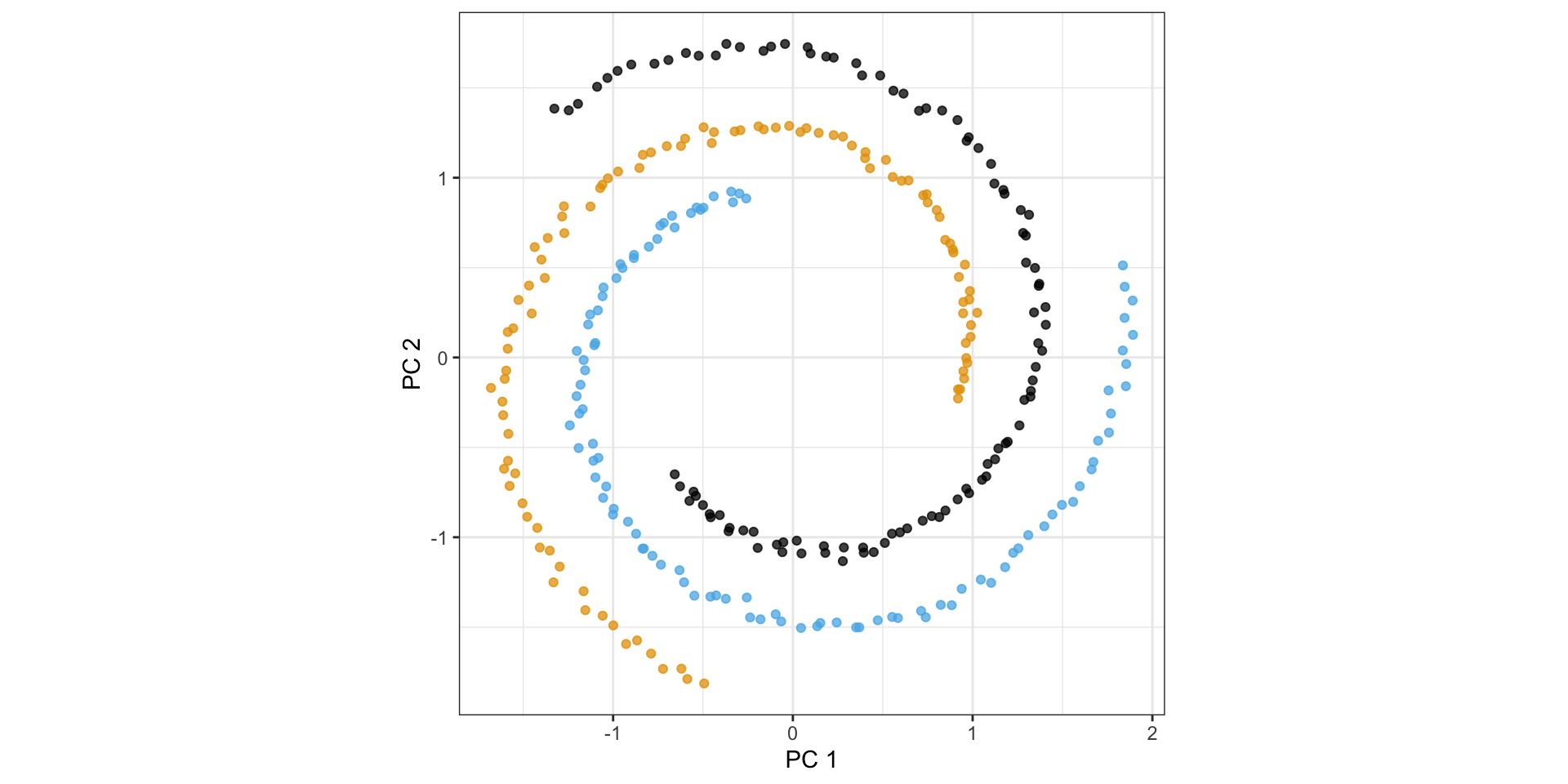
PCA simply rotates the data…
Nonlinear dimension reduction with t-SNE
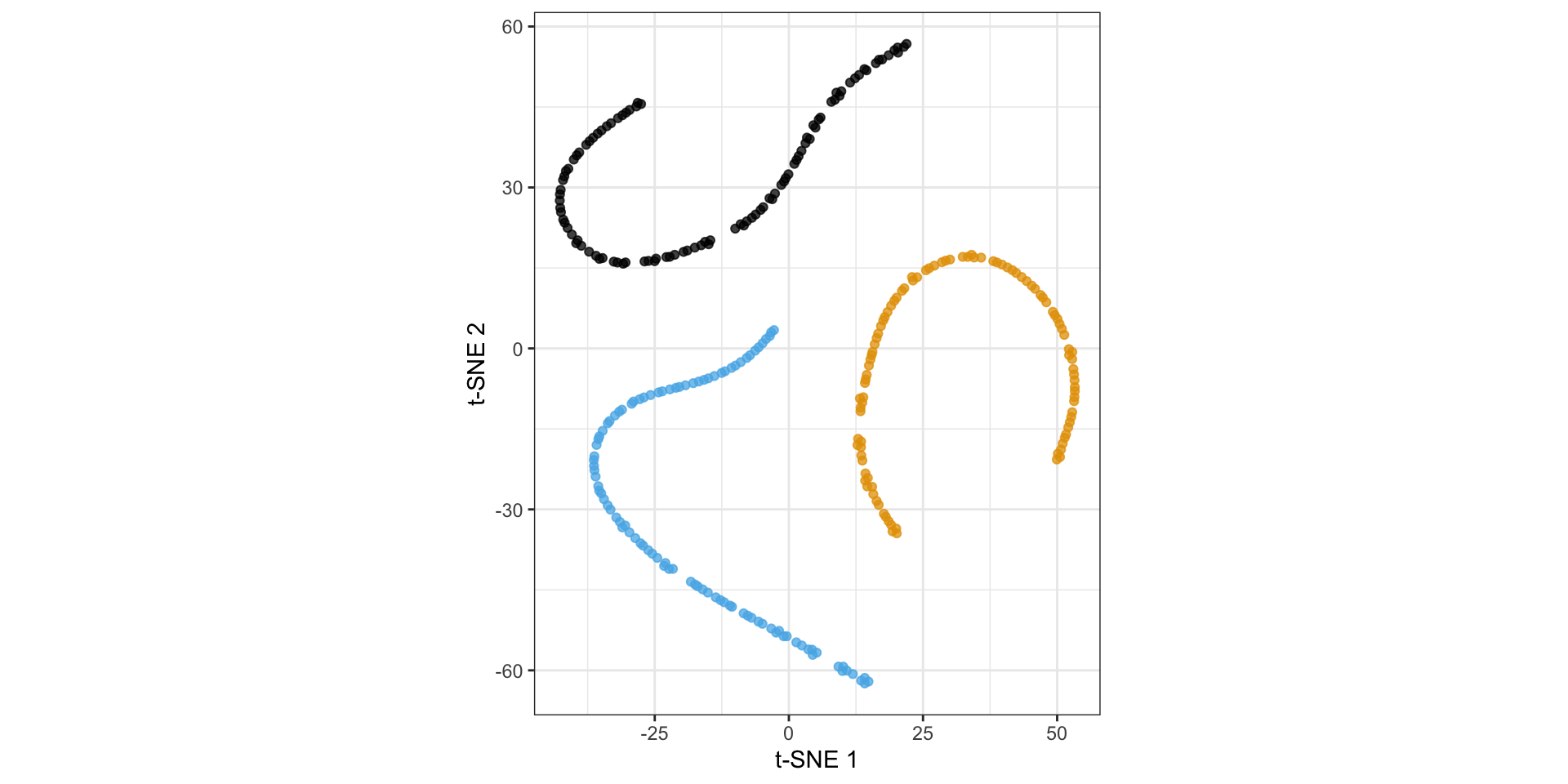
t-distributed stochastic neighbor embedding
- Construct conditional probability for similarity between observations in original space, i.e., probability \(x_i\) will pick \(x_j\) as its neighbor
\[p_{j \mid i}=\frac{\exp \left(-\left\|x_i-x_j\right\|^2 / 2 \sigma_i^2\right)}{\sum_{k \neq i} \exp \left(-\left\|x_i-x_k\right\|^2 / 2 \sigma_i^2\right)},\quad p_{i j}=\frac{\left(p_{j \mid i}+p_{i \mid j}\right)}{2 n}\]
- \(\sigma_i\) is the variance of Gaussian centered at \(x_i\) controlled by perplexity: \(\log (\text { perplexity })=-\sum_j p_{j \mid i} \log _2 p_{j \mid i}\)
t-distributed stochastic neighbor embedding
- Find points \(y_i\) in lower dimensional space with symmetrized student t-distribution
\[q_{j \mid i}=\frac{\left(1+\left\|y_i-y_j\right\|^2\right)^{-1}}{\sum_{k \neq i}\left(1+\left\|y_i-y_k\right\|^2\right)^{-1}}, \quad q_{i j}=\frac{q_{i \mid j}+q_{j \mid i}}{2 n}\]
- Match conditional probabilities by minimize sum of KL divergences \(C=\sum_{i j} p_{i j} \log \left(\frac{p_{i j}}{q_{i j}}\right)\)
Starbucks t-SNE plot with Rtsne
Starbucks t-SNE plot with Rtsne
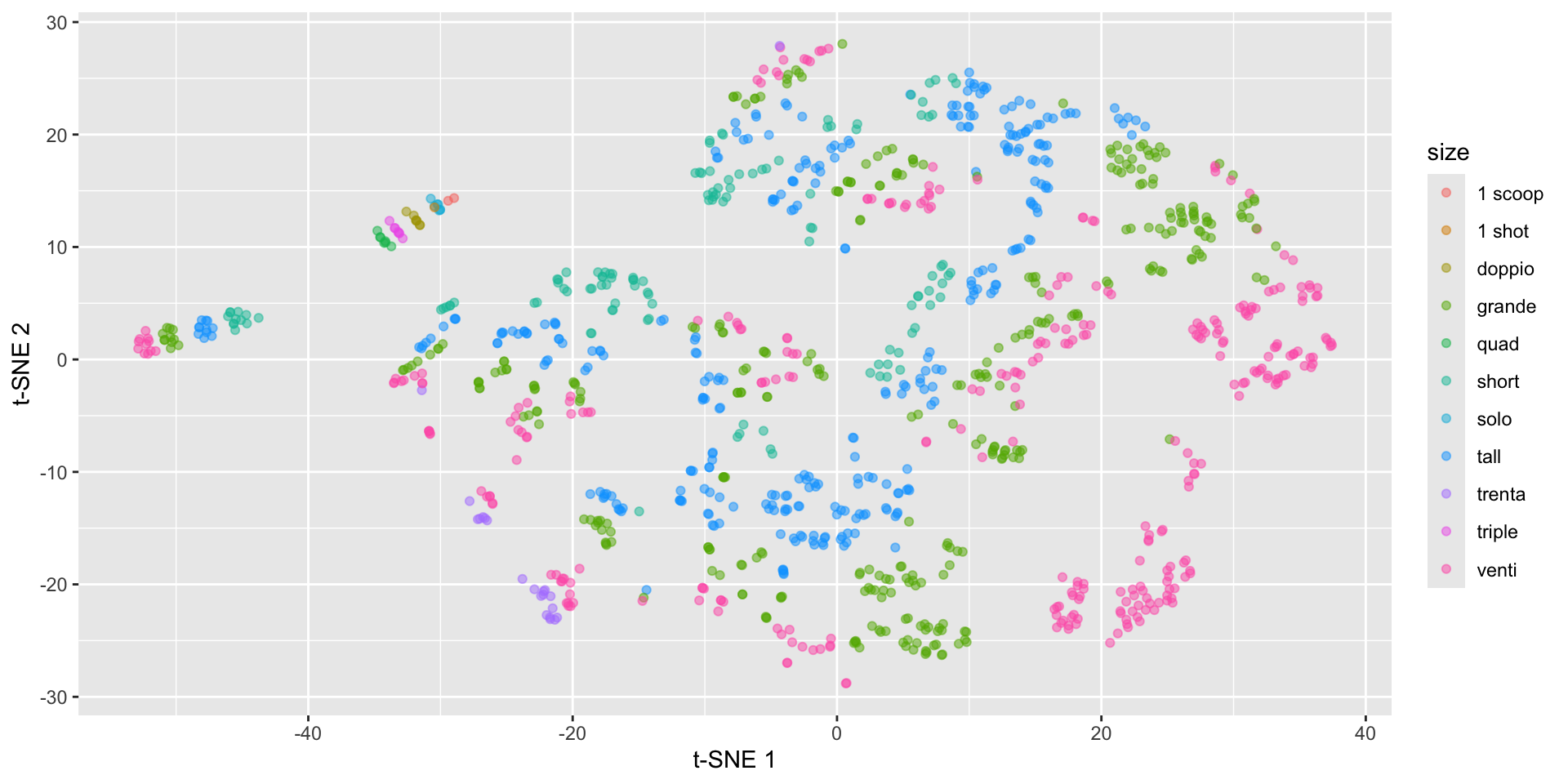
Starbucks t-SNE plot - involves randomness!
set.seed(2014)
tsne_fit <- starbucks |>
dplyr::select(serv_size_m_l:caffeine_mg) |>
scale() |>
Rtsne(check_duplicates = FALSE)
starbucks |>
mutate(tsne1 = tsne_fit$Y[,1],
tsne2 = tsne_fit$Y[,2]) |>
ggplot(aes(x = tsne1, y = tsne2,
color = size)) +
geom_point(alpha = 0.5) +
labs(x = "t-SNE 1", y = "t-SNE 2")Starbucks t-SNE plot - involves randomness!
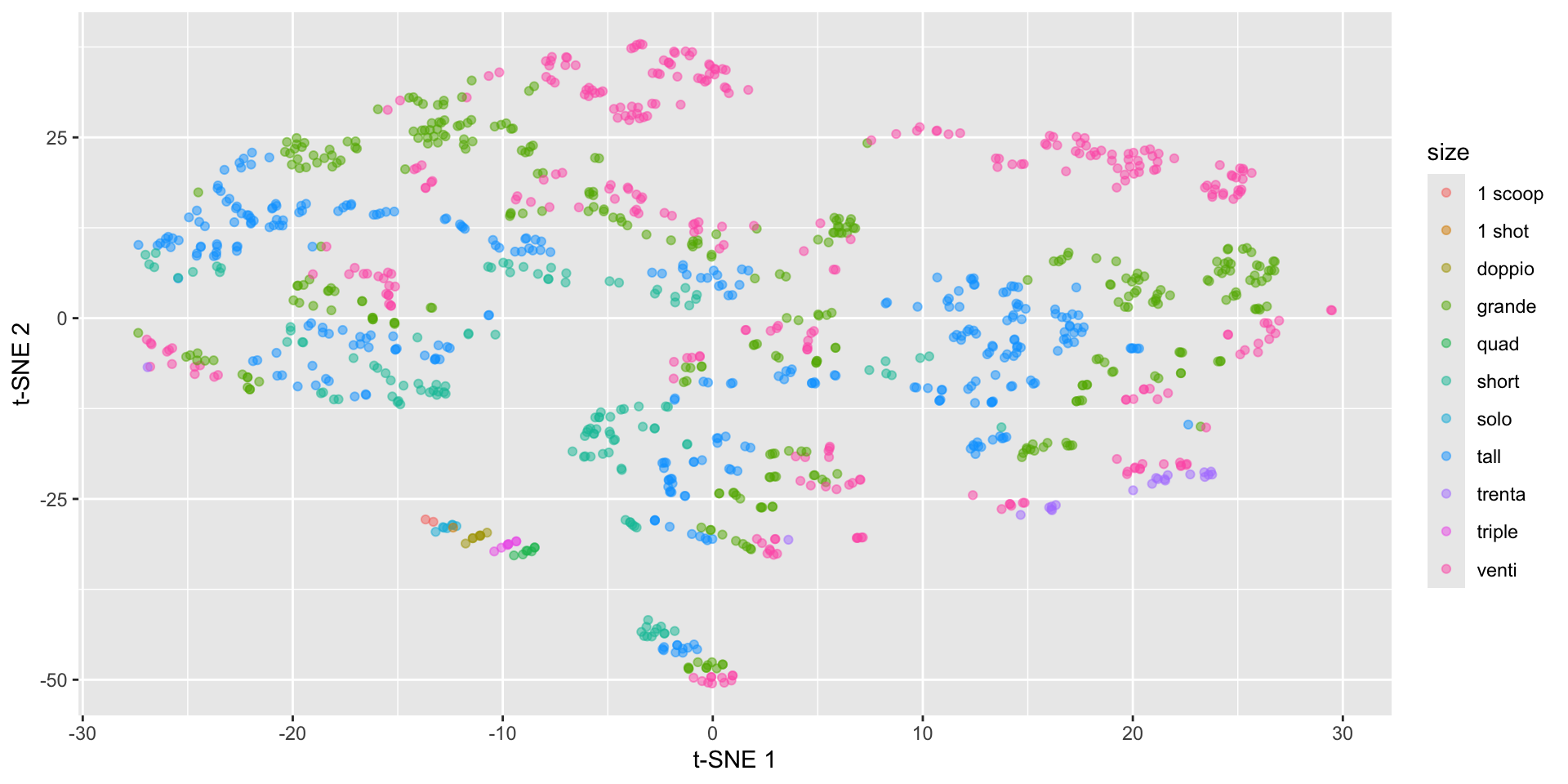
Starbucks t-SNE plot - watch the perplexity!
set.seed(2013)
tsne_fit <- starbucks |>
dplyr::select(serv_size_m_l:caffeine_mg) |>
scale() |>
Rtsne(perplexity = 100,
check_duplicates = FALSE)
starbucks |>
mutate(tsne1 = tsne_fit$Y[,1],
tsne2 = tsne_fit$Y[,2]) |>
ggplot(aes(x = tsne1, y = tsne2,
color = size)) +
geom_point(alpha = 0.5) +
labs(x = "t-SNE 1", y = "t-SNE 2")Starbucks t-SNE plot - watch the perplexity!
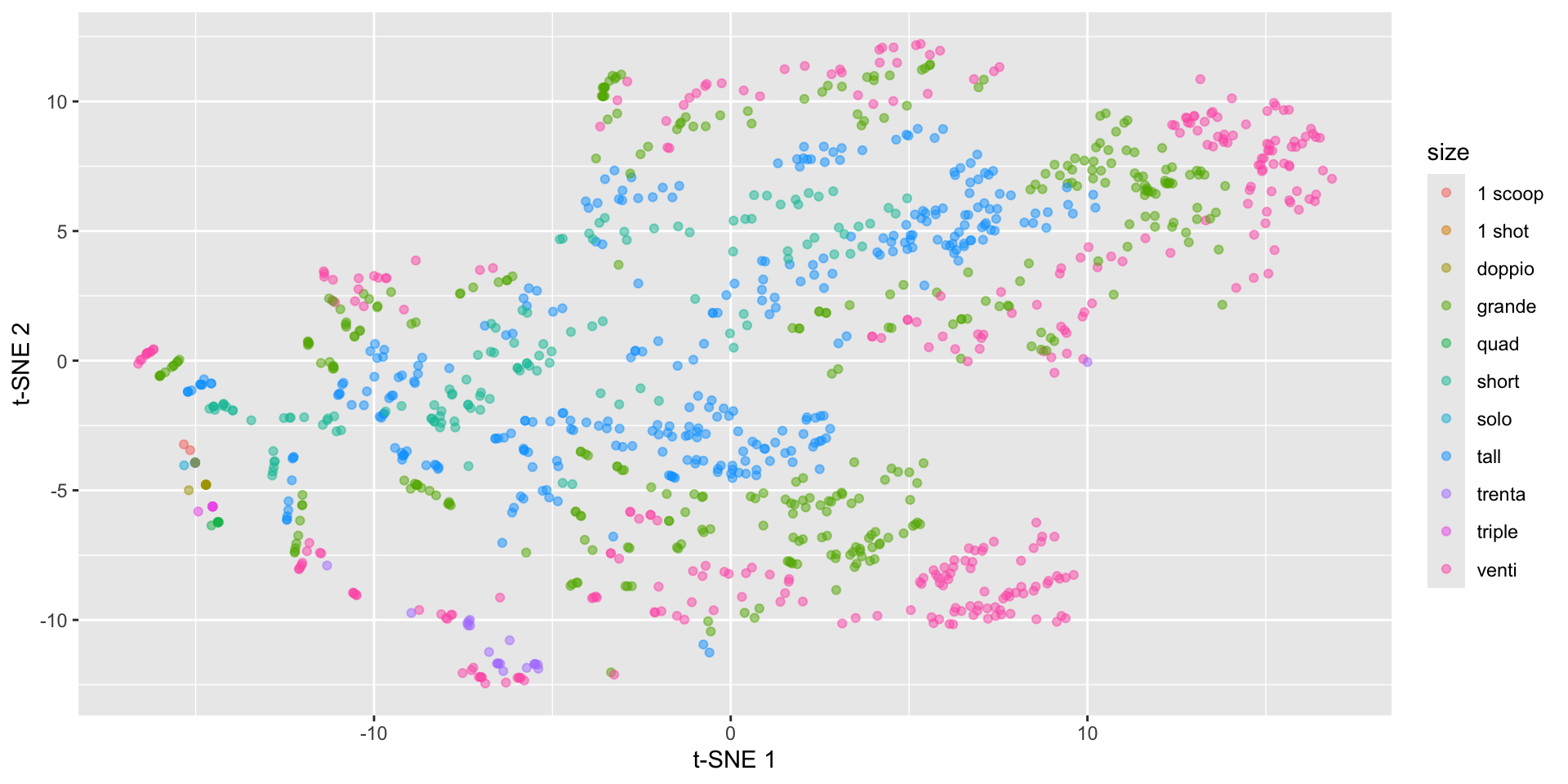
Back to the spirals: results depend on perplexity!
Criticisms of t-SNE plots
Poor scalability: does not scale well for large data, can practically only embed into 2 or 3 dimensions
Meaningless global structure: distance between clusters might not have clear interpretation and cluster size doesn’t have any meaning to it
Poor performance with very high dimensional data: need PCA as pre-dimension reduction step
Sometime random noise can lead to false positive structure in the t-SNE projection
Can NOT interpret like PCA!
Longitudinal data and time series structure
- Consider a single observation measured across time
| Variable | \(T_1\) | \(T_2\) | \(\dots\) | \(T_J\) |
|---|---|---|---|---|
| \(X_1\) | \(x_{11}\) | \(x_{12}\) | \(\dots\) | \(x_{1J}\) |
| \(X_2\) | \(x_{21}\) | \(x_{22}\) | \(\dots\) | \(x_{2J}\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\dots\) | \(\vdots\) |
| \(X_P\) | \(x_{P1}\) | \(x_{P2}\) | \(\dots\) | \(x_{PJ}\) |
With \(N\) observations we have \(N\) of these matrices
Time may consist of regularly spaced intervals
- For example, \(T_1 = t\), \(T_2 = t + h\), \(T_3 = t + 2h\), etc.
Irregularly spaced intervals, then work with the raw \(T_1,T_2,...\)
Example: Statistics PhDs by year
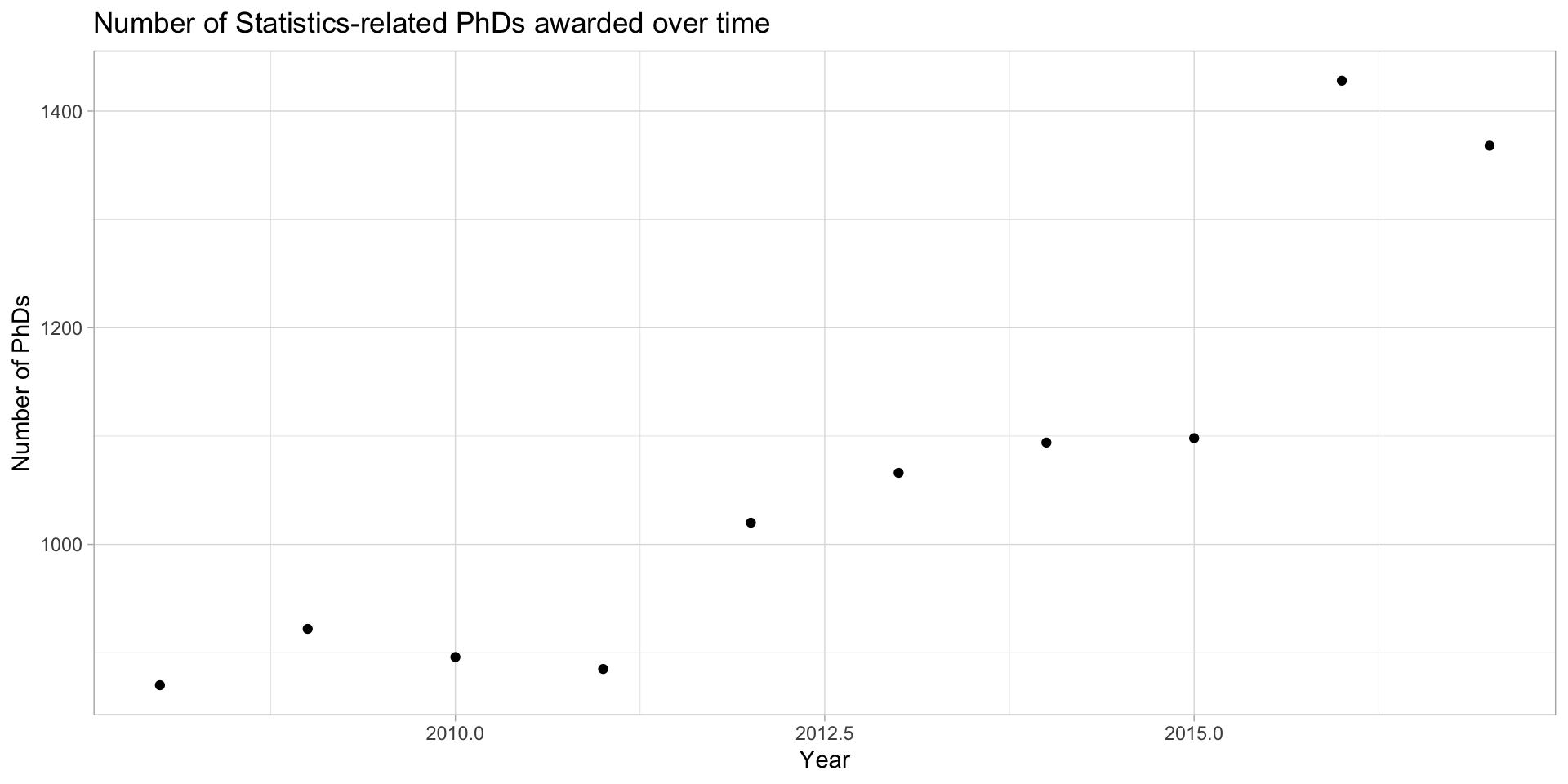
Example: Statistics PhDs by year
stat_phd_year_summary |>
ggplot(aes(x = year, y = n_phds)) +
geom_point() +
scale_x_continuous(breaks = unique(stat_phd_year_summary$year),
labels = unique(stat_phd_year_summary$year)) +
theme_light() +
labs(x = "Year", y = "Number of PhDs", title = "Number of Statistics-related PhDs awarded over time")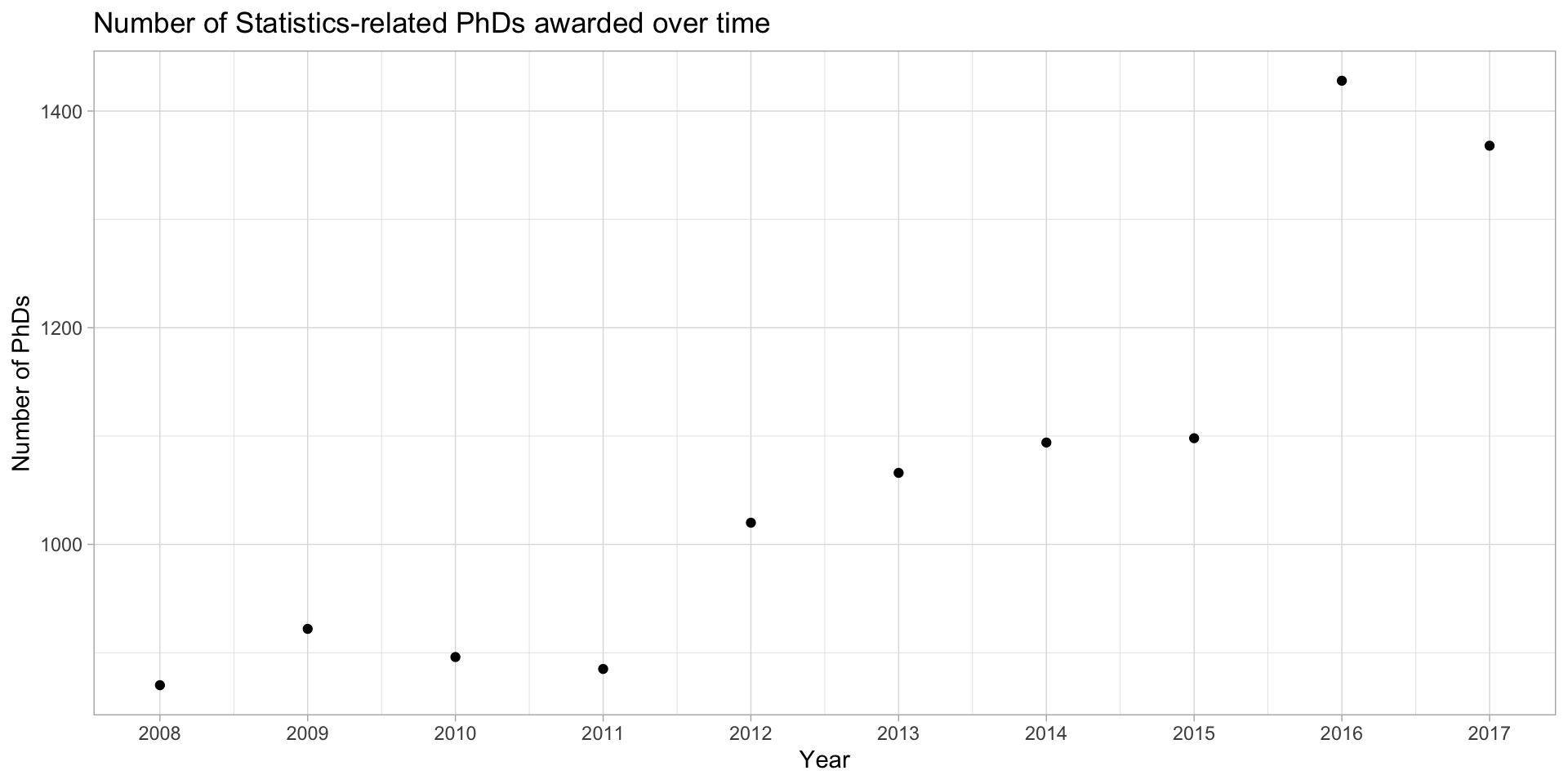
Add lines to emphasize order
stat_phd_year_summary |>
ggplot(aes(x = year, y = n_phds)) +
geom_point() +
geom_line() +
scale_x_continuous(breaks = unique(stat_phd_year_summary$year),
labels = unique(stat_phd_year_summary$year)) +
theme_light() +
labs(x = "Year", y = "Number of PhDs",
title = "Number of Statistics-related PhDs awarded over time")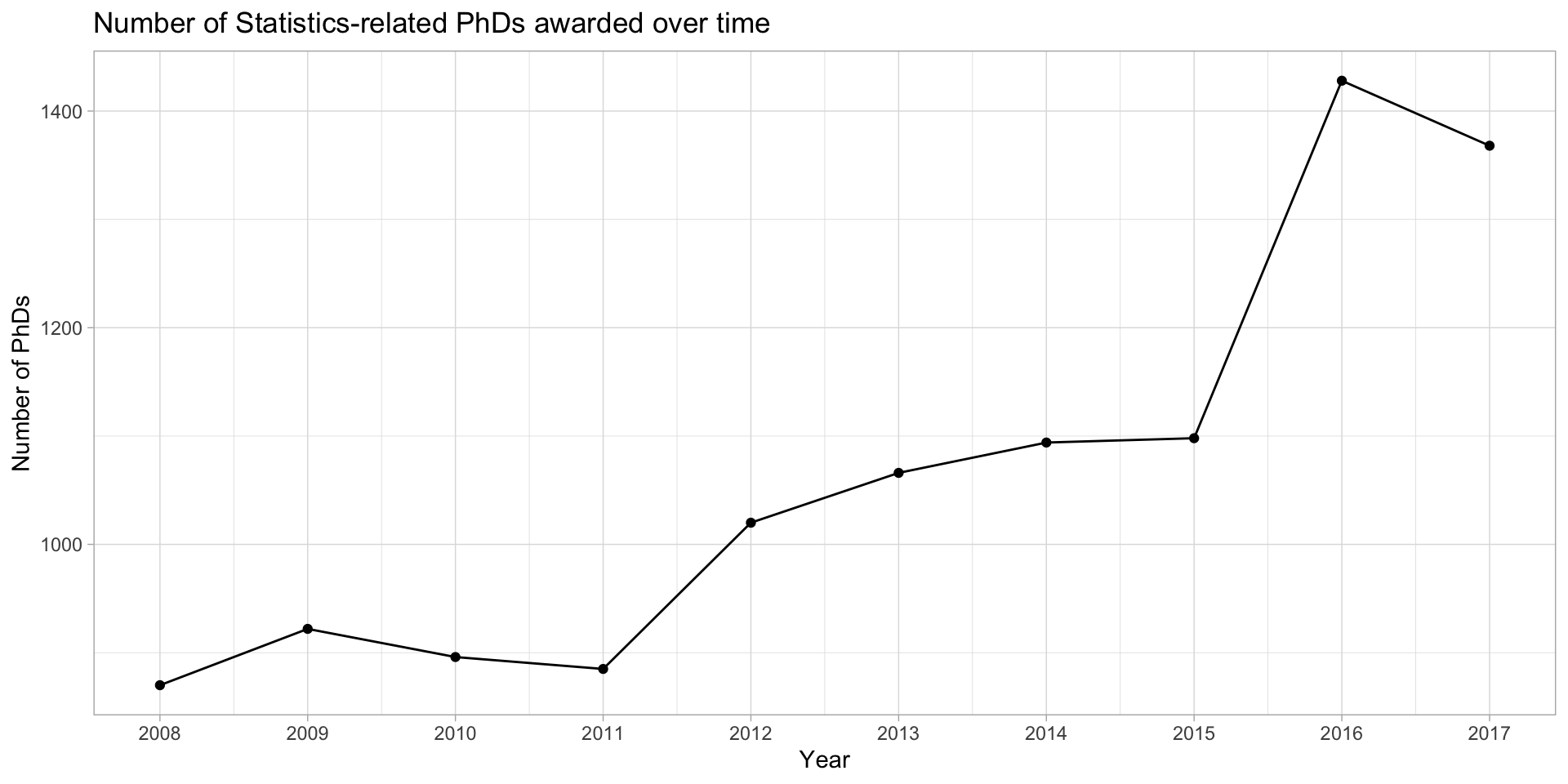
Drop points to emphasize trends
stat_phd_year_summary |>
ggplot(aes(x = year, y = n_phds)) +
geom_line() +
scale_x_continuous(breaks = unique(stat_phd_year_summary$year),
labels = unique(stat_phd_year_summary$year)) +
theme_light() +
labs(x = "Year", y = "Number of PhDs",
title = "Number of Statistics-related PhDs awarded over time")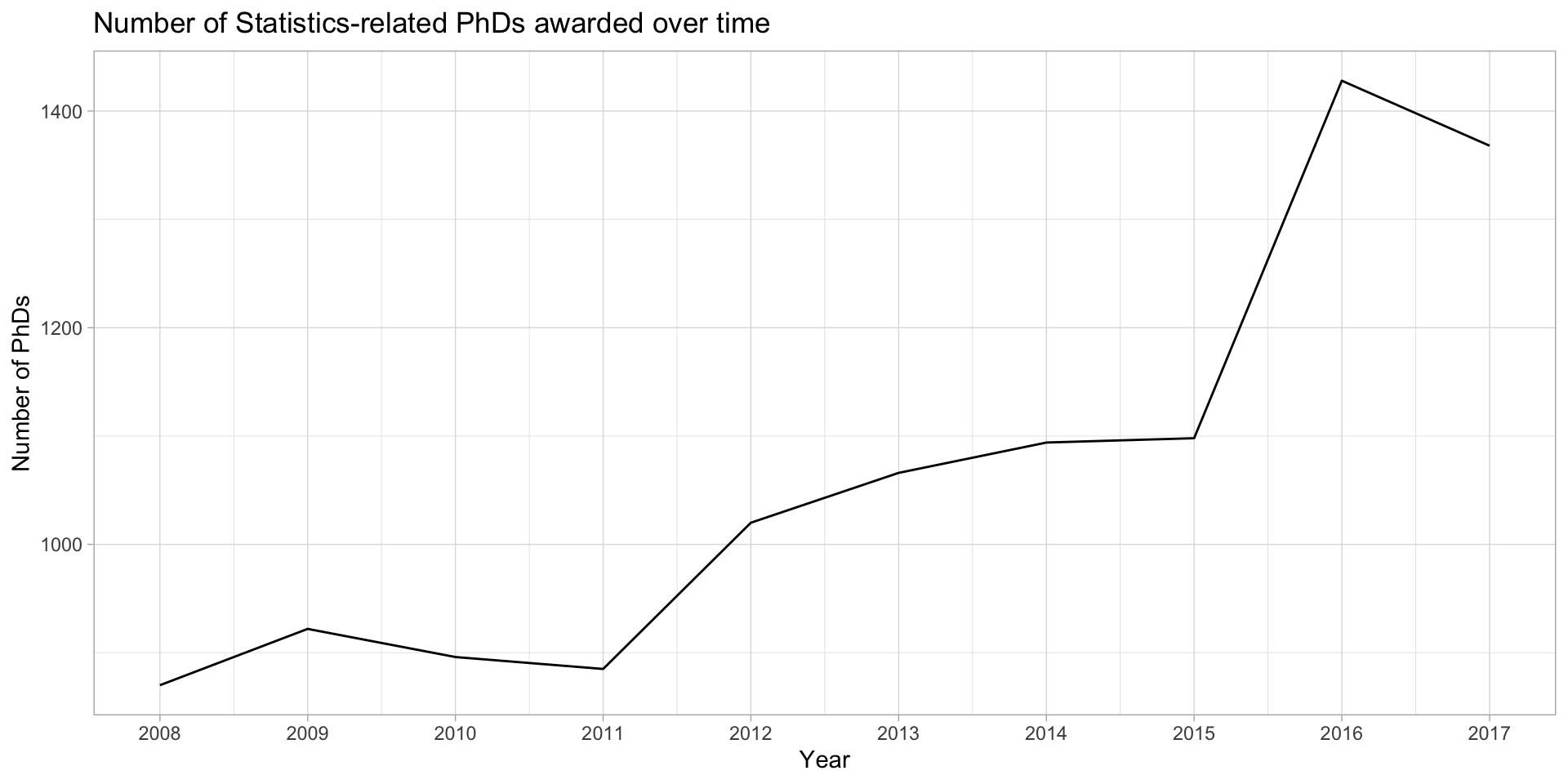
Can fill the area under the line
stat_phd_year_summary |>
ggplot(aes(x = year, y = n_phds)) +
geom_area(fill = "darkblue", alpha = 0.5) +
geom_line() +
scale_x_continuous(breaks = unique(stat_phd_year_summary$year),
labels = unique(stat_phd_year_summary$year)) +
theme_light() +
labs(x = "Year", y = "Number of PhDs",
title = "Number of Statistics-related PhDs awarded over time")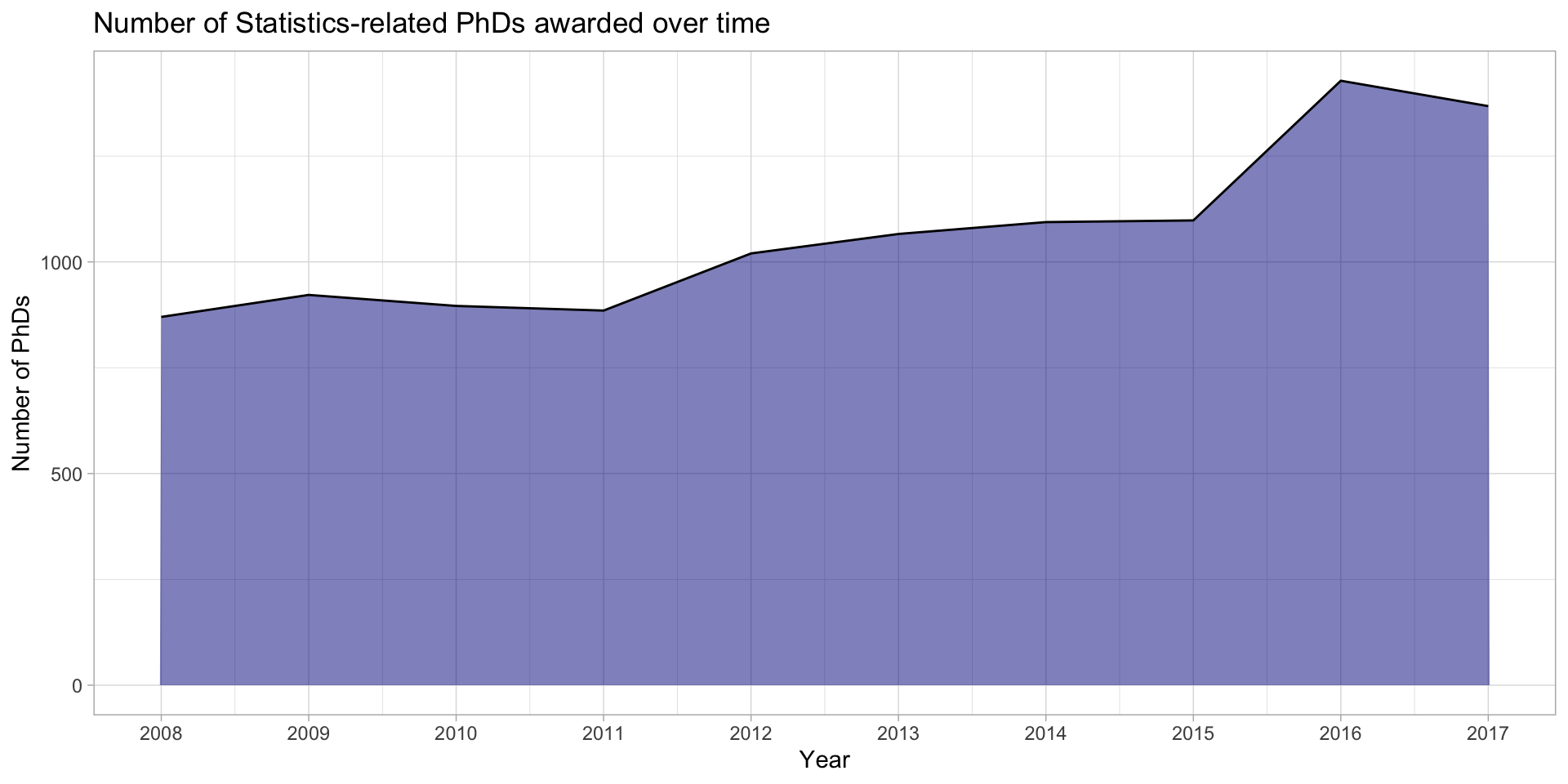
Several time series? Do NOT only use points
stats_phds |>
ggplot(aes(x = year, y = n_phds, color = field)) +
geom_point() +
scale_x_continuous(breaks = unique(stat_phd_year_summary$year),
labels = unique(stat_phd_year_summary$year)) +
theme_light() +
theme(legend.position = "bottom", legend.text = element_text(size = 7)) +
labs(x = "Year", y = "Number of PhDs",
title = "Number of Statistics-related PhDs awarded over time",
color = "Field")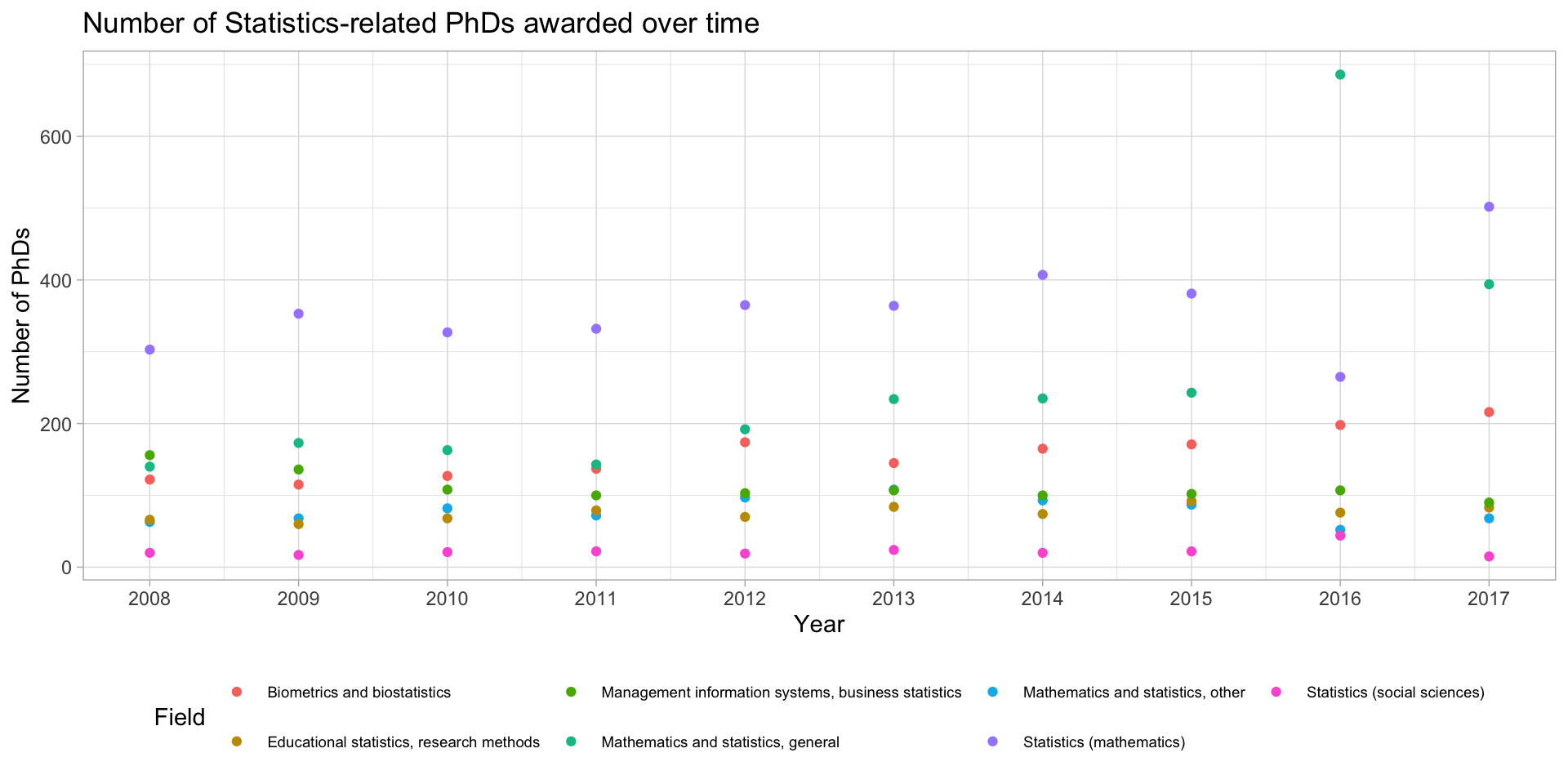
Several time series? Use lines!
stats_phds |>
ggplot(aes(x = year, y = n_phds, color = field)) +
geom_line() +
scale_x_continuous(breaks = unique(stat_phd_year_summary$year),
labels = unique(stat_phd_year_summary$year)) +
theme_light() +
theme(legend.position = "bottom") +
labs(x = "Year", y = "Number of PhDs", color = "Field",
title = "Number of Statistics-related PhDs awarded over time")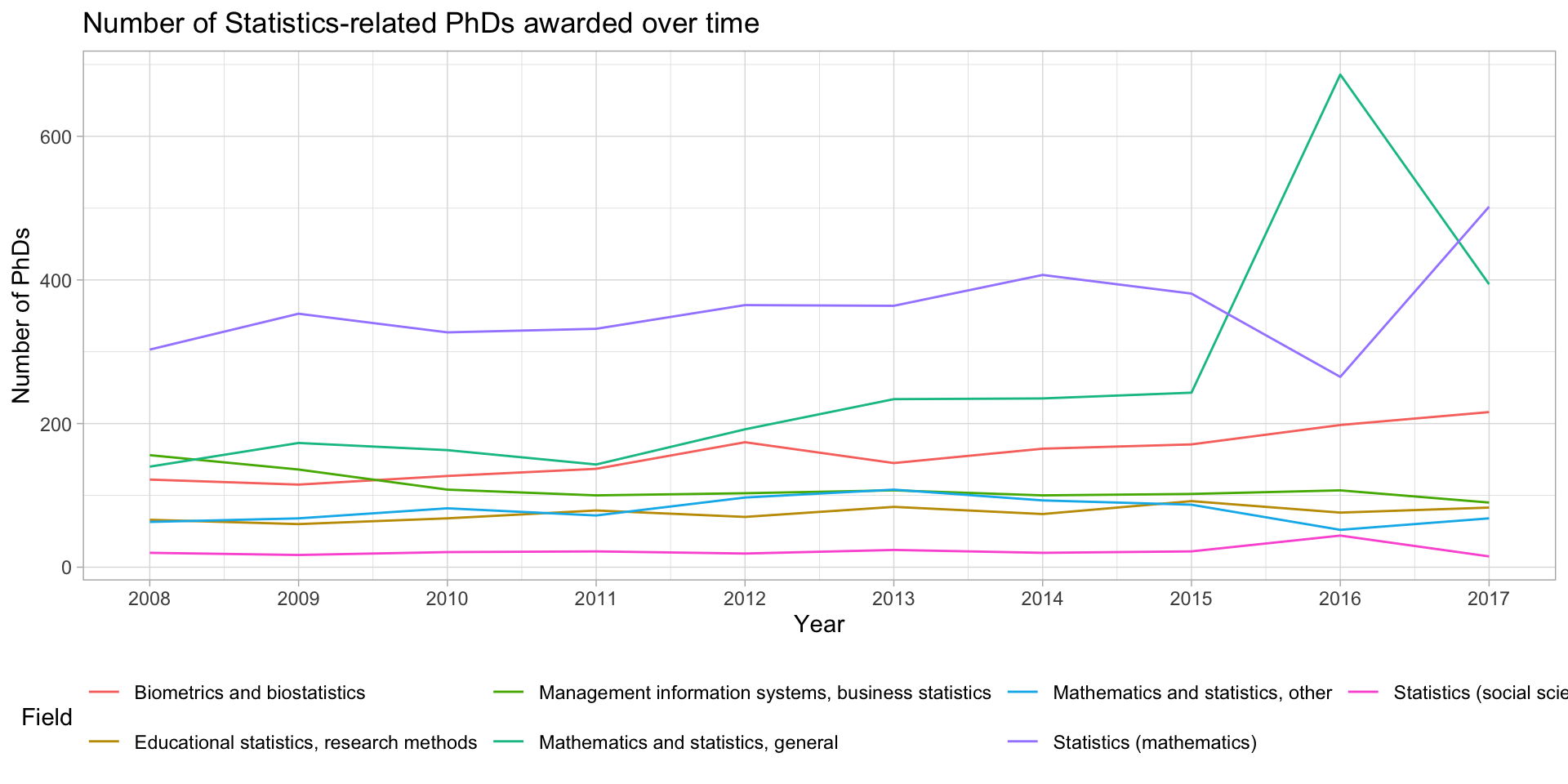
Using ggrepel to directly label lines
stats_phds_2017 <- stats_phds |> filter(year == 2017)
library(ggrepel)
stats_phds |>
ggplot(aes(x = year, y = n_phds, color = field)) +
geom_line() +
# Add the labels:
geom_text_repel(data = stats_phds_2017, aes(label = field),
size = 3,
# Drop the segment connection:
segment.color = NA,
# Move labels up or down based on overlap
direction = "y",
# Try to align the labels horizontally on the left hand side
hjust = "left") +
scale_x_continuous(breaks = unique(stat_phd_year_summary$year),
labels = unique(stat_phd_year_summary$year),
# Update the limits so that there is some padding on the
# x-axis but don't label the new maximum
limits = c(min(stat_phd_year_summary$year),
max(stat_phd_year_summary$year) + 3)) +
theme_light() +
theme(legend.position = "none") +
labs(x = "Year", y = "Number of PhDs", color = "Field",
title = "Number of Statistics-related PhDs awarded over time")Using ggrepel to directly label lines
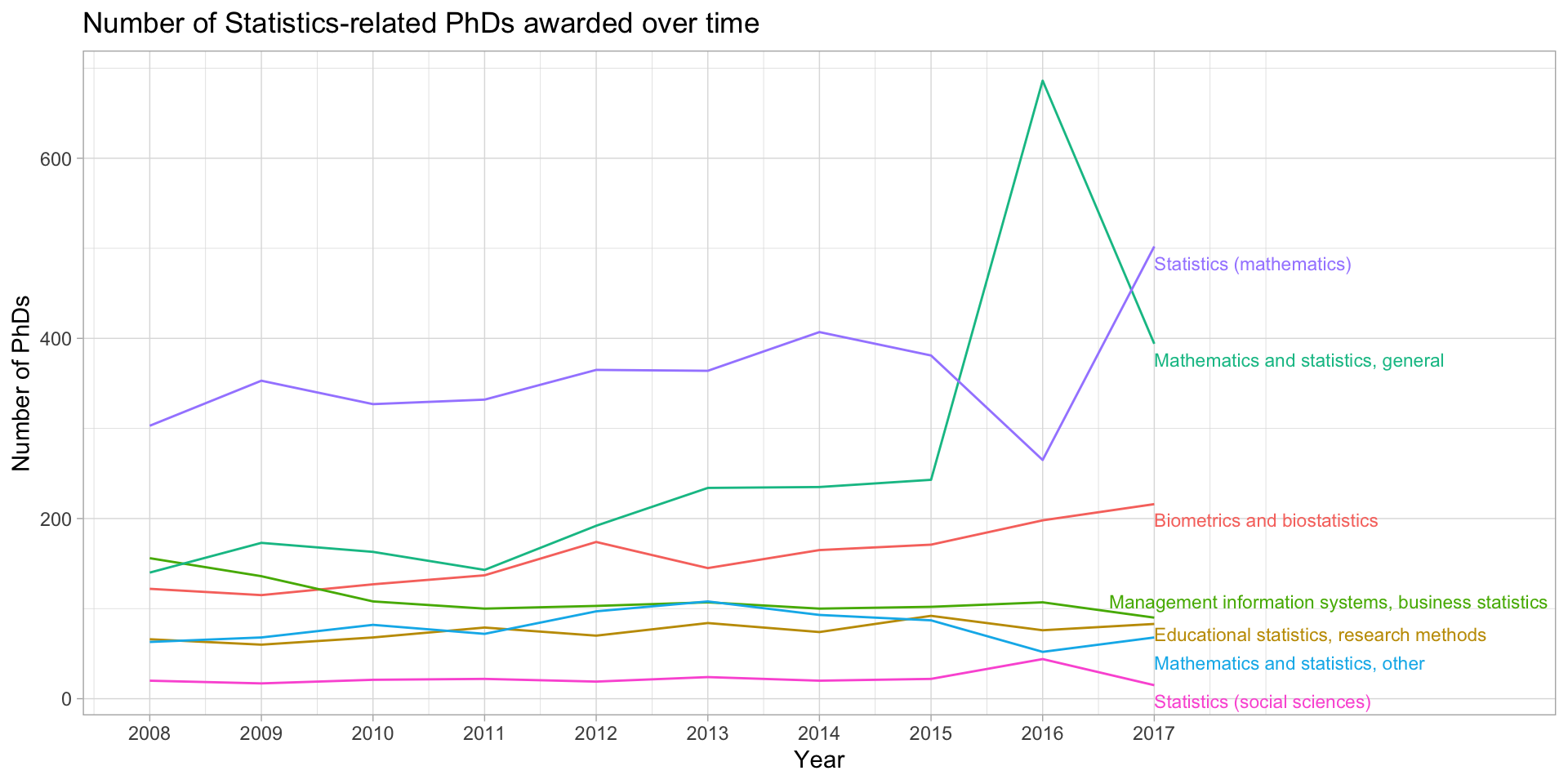
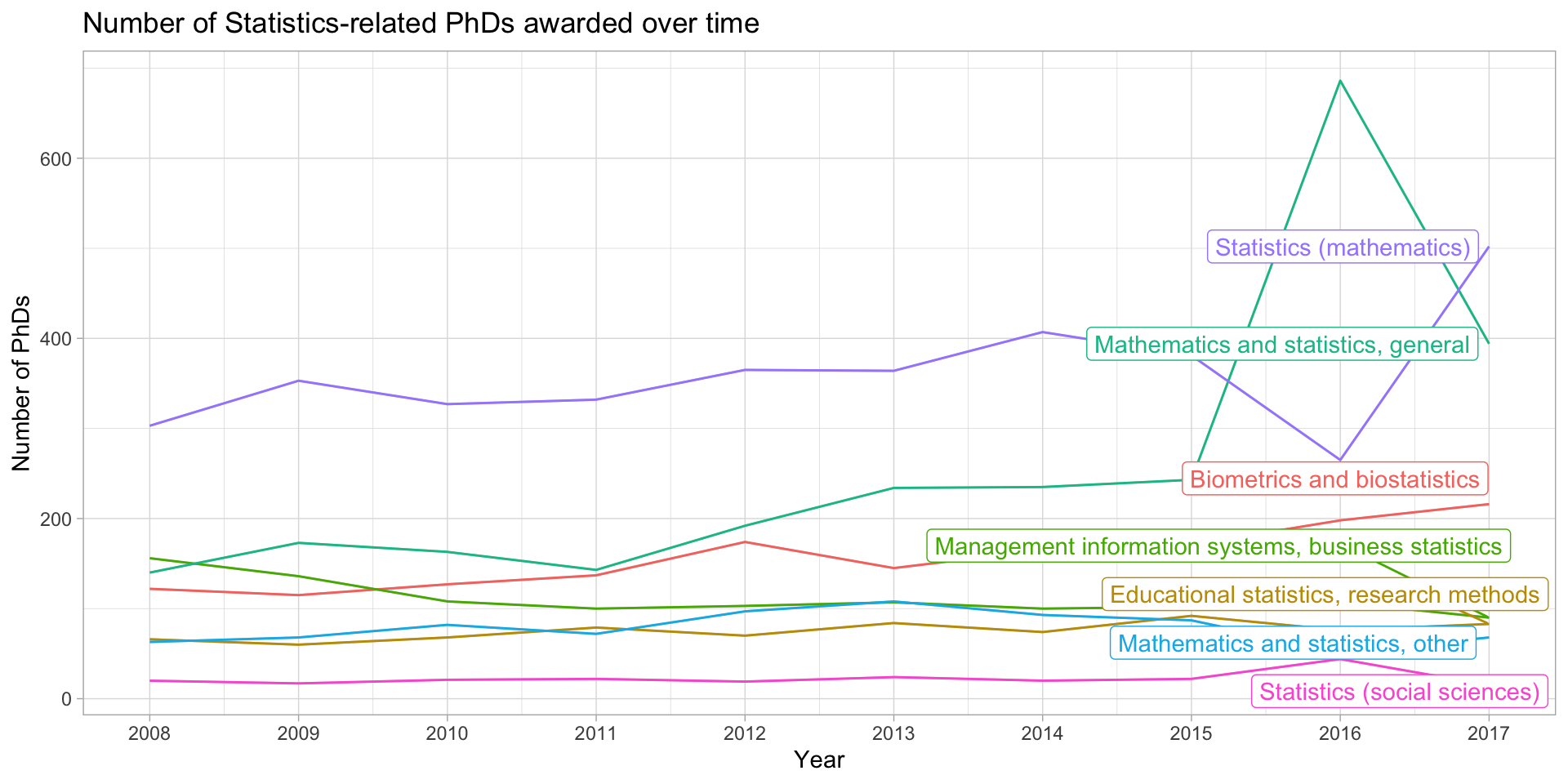
Using gghighlight instead
library(gghighlight)
stats_phds |>
ggplot(aes(x = year, y = n_phds, color = field)) +
geom_line() +
gghighlight() +
scale_x_continuous(breaks = unique(stat_phd_year_summary$year),
labels = unique(stat_phd_year_summary$year)) +
theme_light() +
theme(legend.position = "none") +
labs(x = "Year", y = "Number of PhDs", color = "Field",
title = "Number of Statistics-related PhDs awarded over time")Using gghighlight instead
Using gghighlight instead
library(gghighlight)
stats_phds |>
ggplot(aes(x = year, y = n_phds, color = field)) +
geom_line() +
gghighlight(line_label_type = "sec_axis") +
scale_x_continuous(breaks = unique(stat_phd_year_summary$year),
labels = unique(stat_phd_year_summary$year)) +
theme_light() +
theme(legend.position = "none") +
labs(x = "Year", y = "Number of PhDs", color = "Field",
title = "Number of Statistics-related PhDs awarded over time")Using gghighlight instead
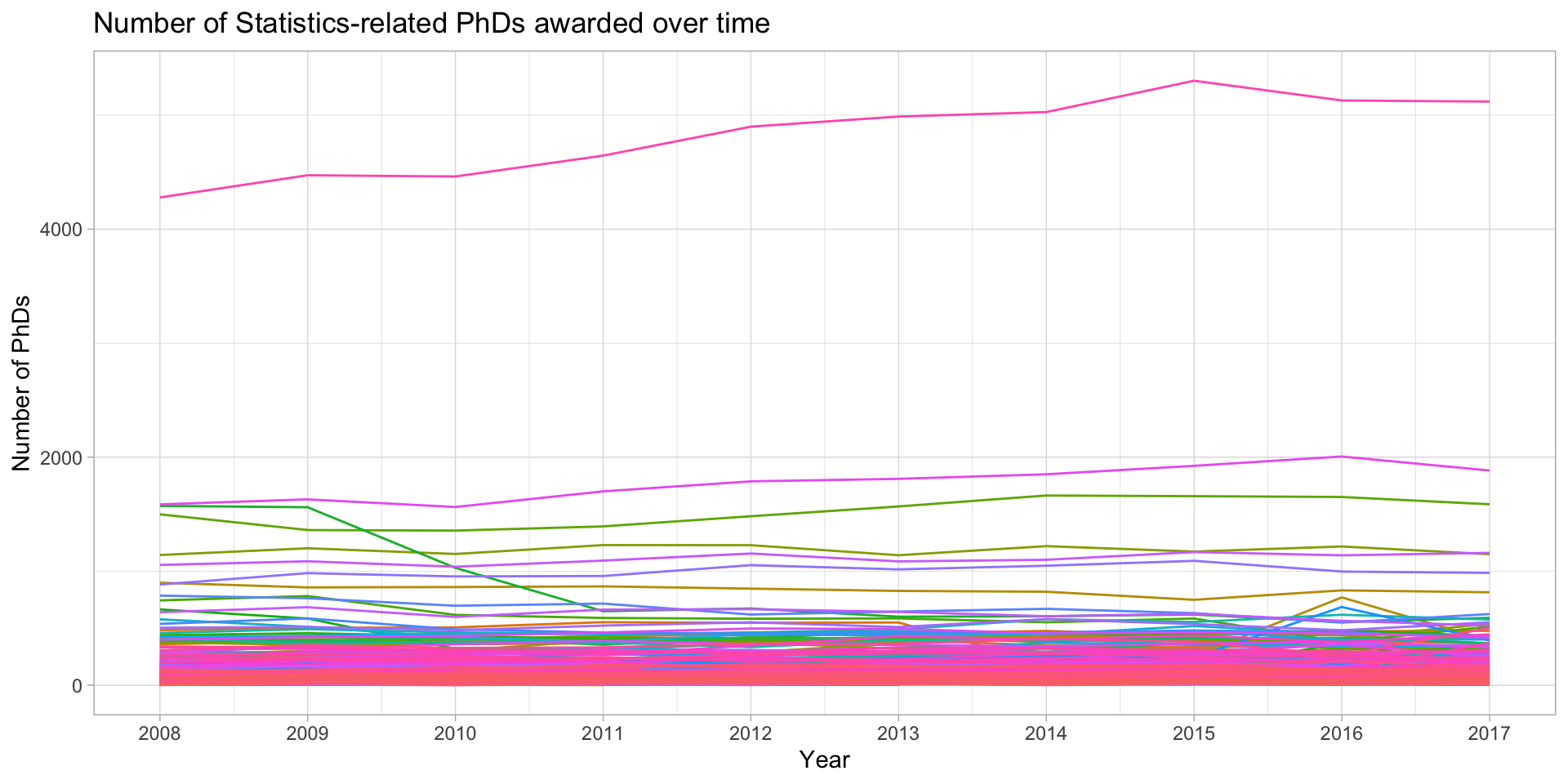
How do we plot many lines? NOT LIKE THIS!
phd_field |>
ggplot(aes(x = year, y = n_phds, color = field)) +
geom_line() +
scale_x_continuous(breaks = unique(stat_phd_year_summary$year),
labels = unique(stat_phd_year_summary$year)) +
theme_light() +
theme(legend.position = "none") +
labs(x = "Year", y = "Number of PhDs", color = "Field",
title = "Number of Statistics-related PhDs awarded over time")How do we plot many lines? NOT LIKE THIS!
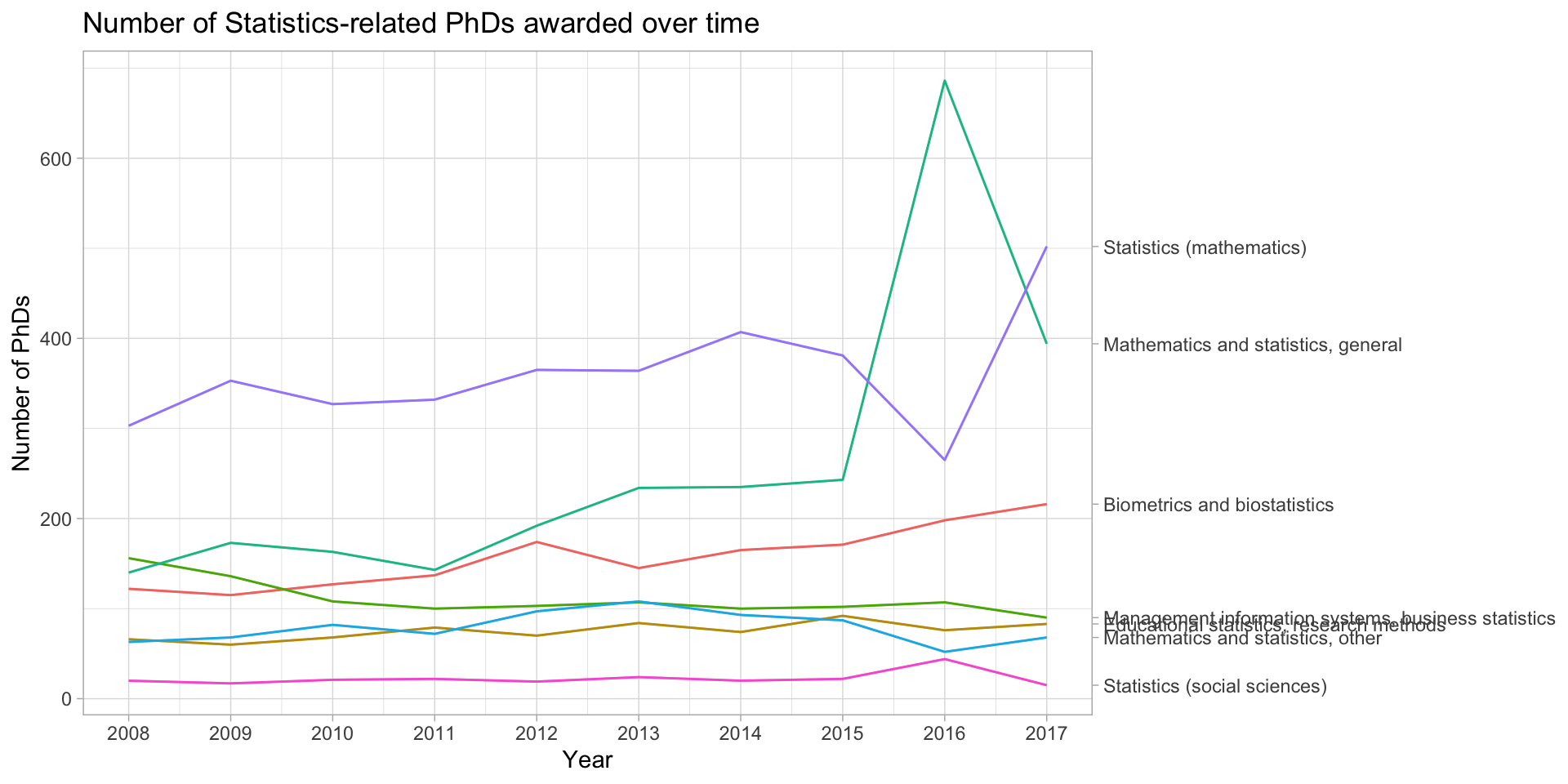
Instead we highlight specific lines
phd_field |>
filter(!(field %in% c("Biometrics and biostatistics", "Statistics (mathematics)"))) |>
ggplot() +
# Add the background lines - need to specify the group to be the field
geom_line(aes(x = year, y = n_phds, group = field),
color = "gray", size = .5, alpha = .5) +
# Now add the layer with the lines of interest:
geom_line(data = filter(phd_field,
# Note this is just the opposite of the above since ! is removed
field %in% c("Biometrics and biostatistics",
"Statistics (mathematics)")),
aes(x = year, y = n_phds, color = field),
# Make the size larger
size = .75, alpha = 1) +
scale_x_continuous(breaks = unique(stat_phd_year_summary$year),
labels = unique(stat_phd_year_summary$year)) +
theme_light() +
theme(legend.position = "bottom",
# Drop the panel lines making the gray difficult to see
panel.grid = element_blank()) +
labs(x = "Year", y = "Number of PhDs", color = "Field",
title = "Number of Statistics-related PhDs awarded over time")Instead we highlight specific lines
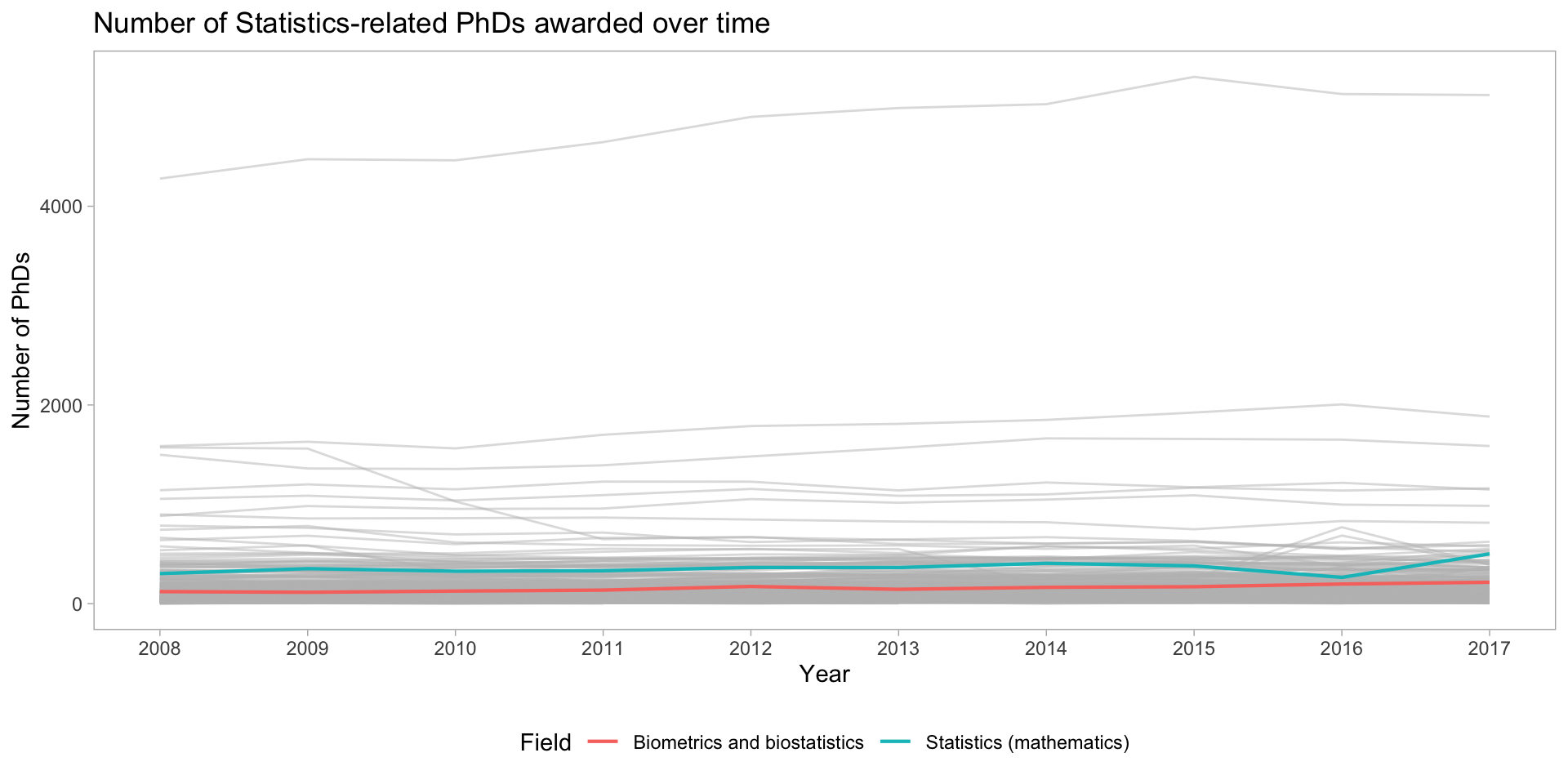
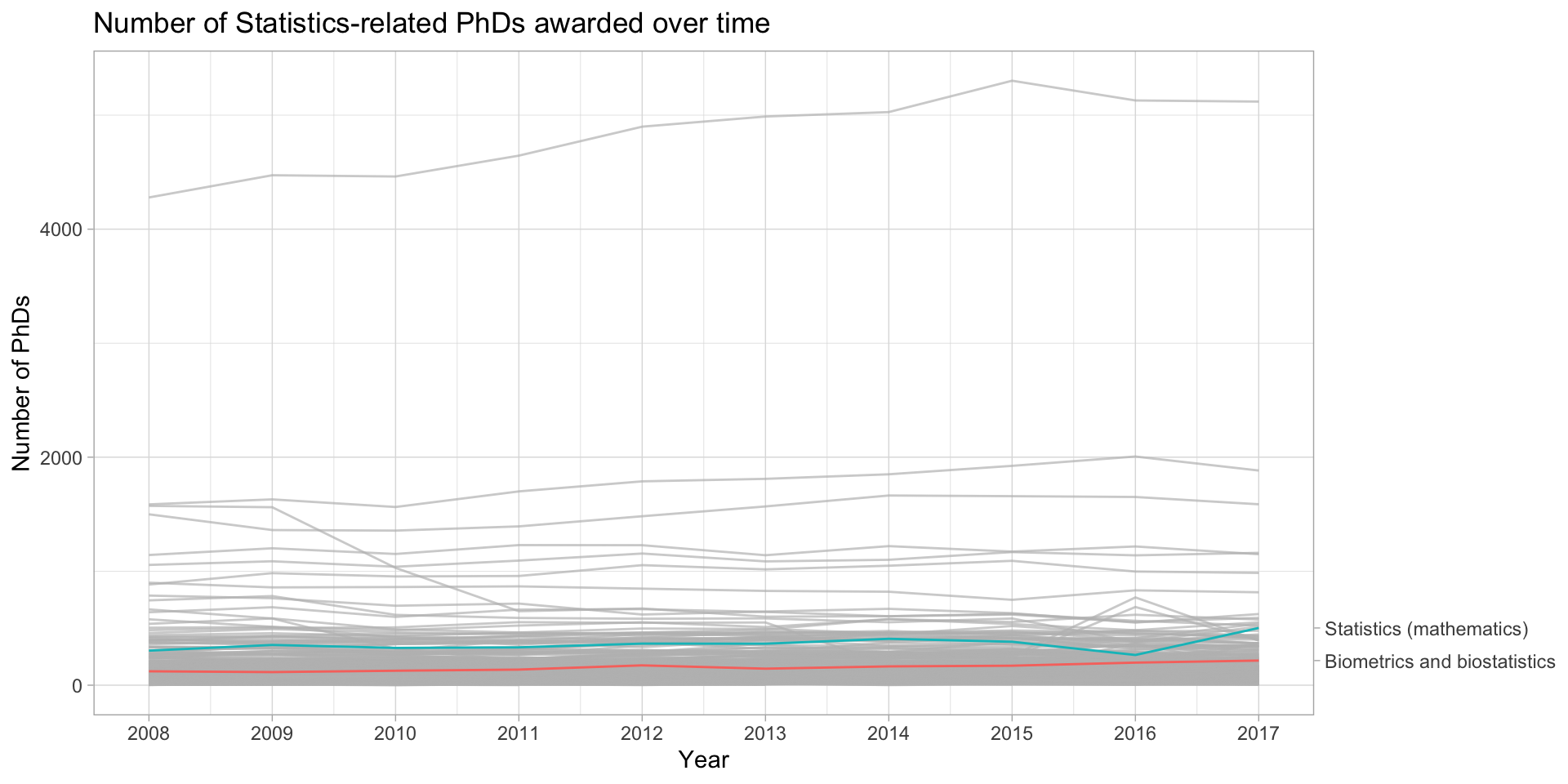
Or you can use gghighlight instead
phd_field |>
ggplot(aes(x = year, y = n_phds, color = field)) +
geom_line() +
gghighlight(field %in% c("Biometrics and biostatistics", "Statistics (mathematics)"),
line_label_type = "sec_axis") +
scale_x_continuous(breaks = unique(stat_phd_year_summary$year),
labels = unique(stat_phd_year_summary$year)) +
theme_light() +
theme(legend.position = "none") +
labs(x = "Year", y = "Number of PhDs", color = "Field",
title = "Number of Statistics-related PhDs awarded over time")Or you can use gghighlight instead
What about Nightingale’s rose diagram?
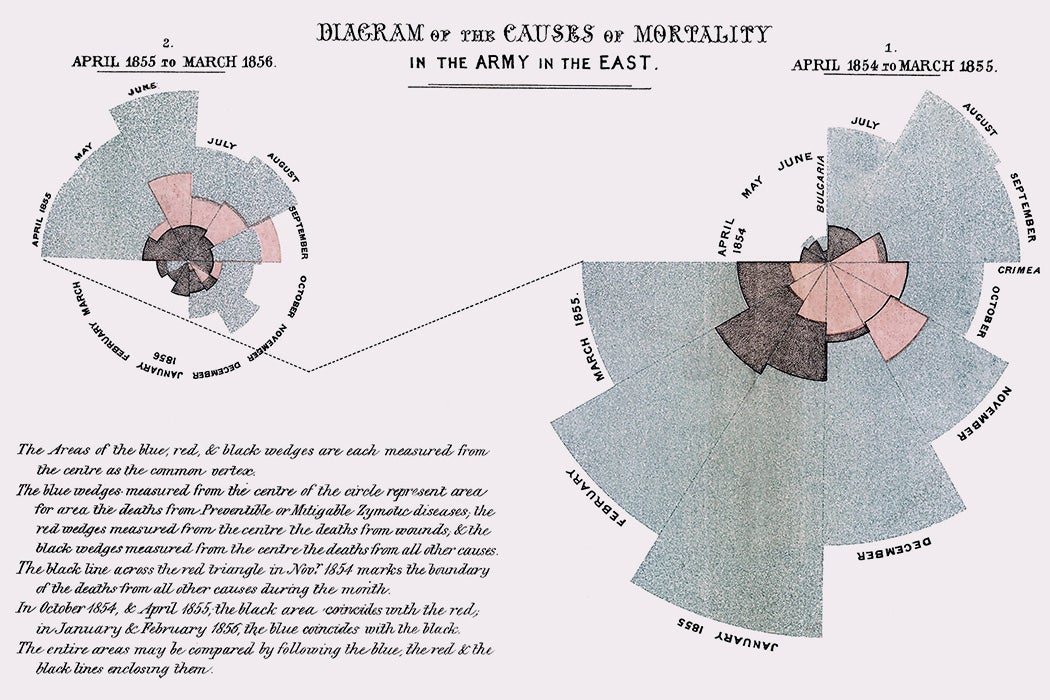
What about Nightingale’s rose diagram?
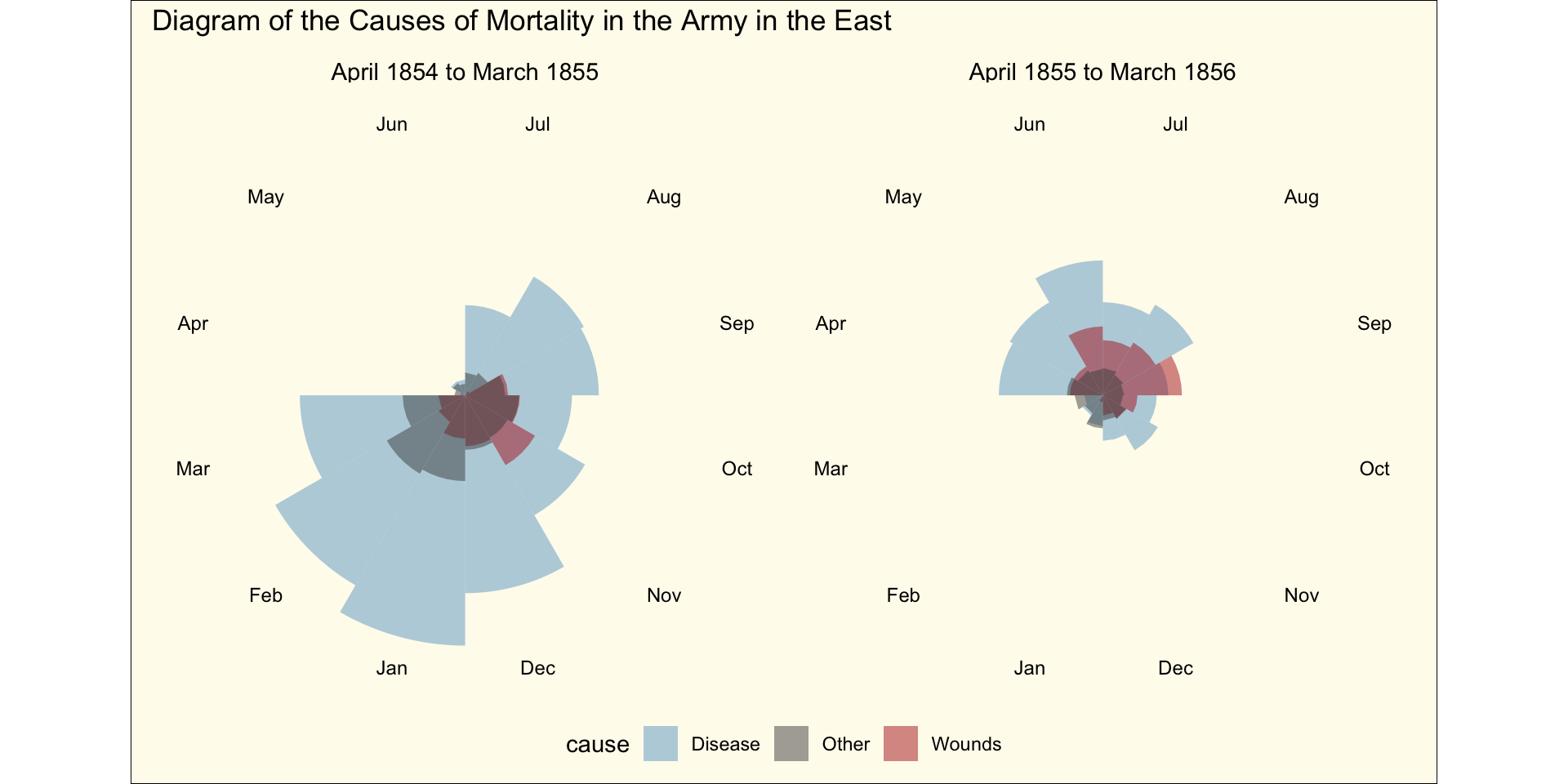
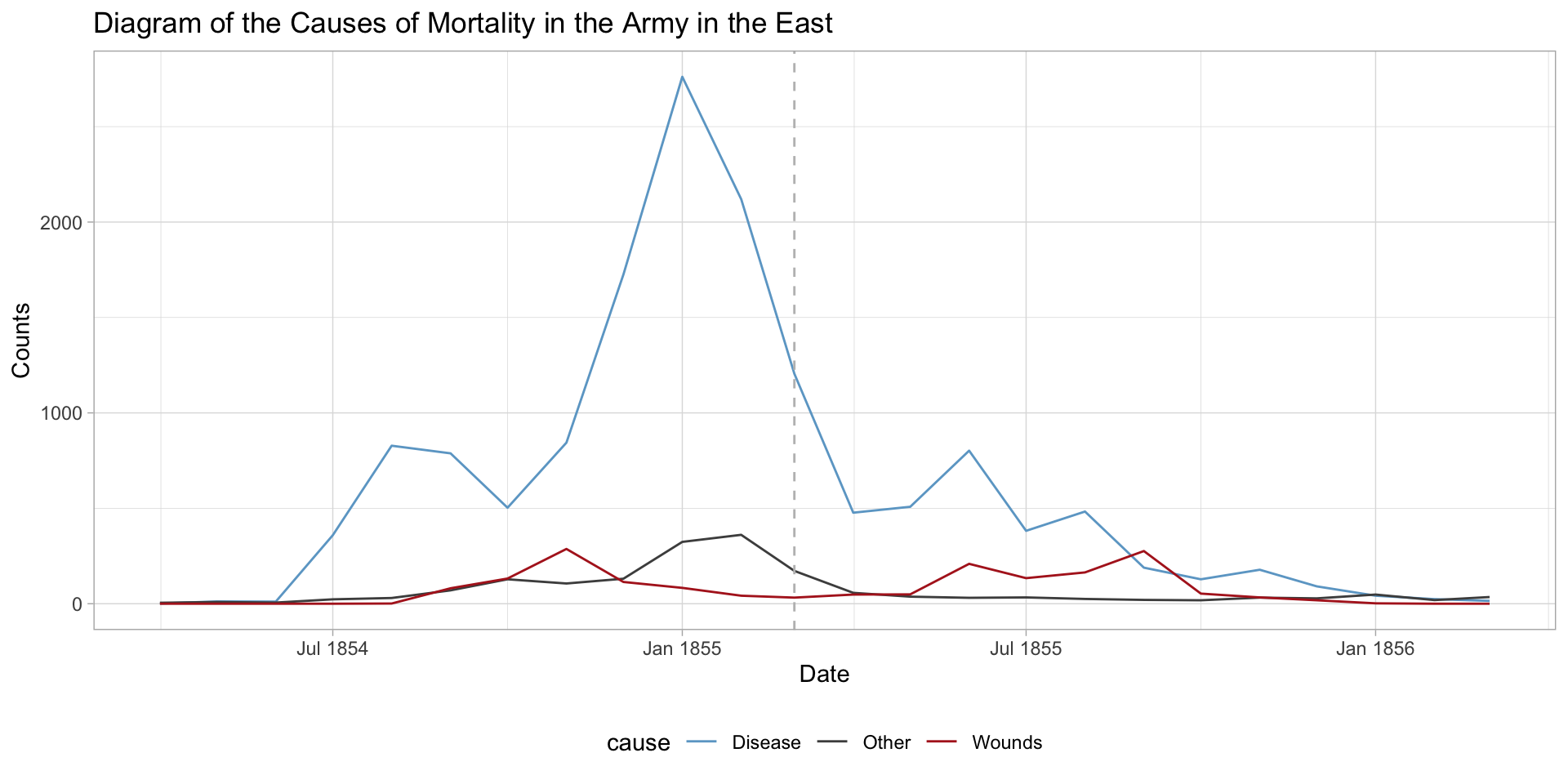
What about displaying lines instead?
Things of interest for time series data
Time series can be characterized by three features:
Trends: Does the variable increase or decrease over time, on average?
Seasonality: Are there changes in the variable that regularly happen (e.g., every winter, every hour, etc.)? Sometimes called periodicity.
Noise: Variation in the variable beyond average trends and seasonality.
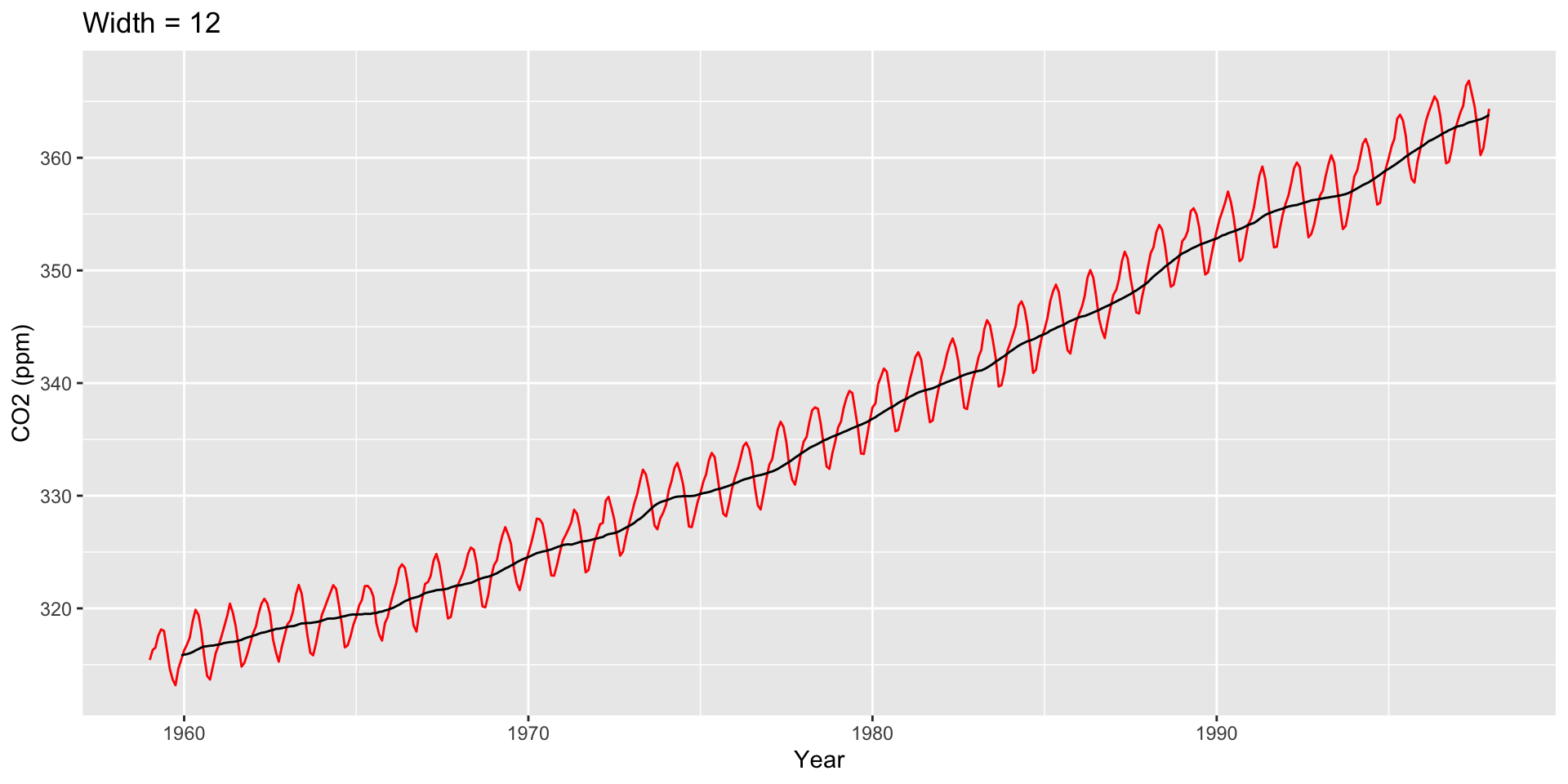
Moving averages are a starting point for visualizing how a trend changes over time

Be responsible with your axes!

Be responsible with your axes!

Moving Average Plots
The Financial Times COVID-19 plots displayed a moving average (sometimes called a rolling average)
Intuition
Divide your data into small subsets (“windows”)
Compute the average within each window
Connect the averages together to make a trend line
Sometimes called a simple moving average
This is exactly what we did with LOESS… we called this a sliding window, but it’s the same thing
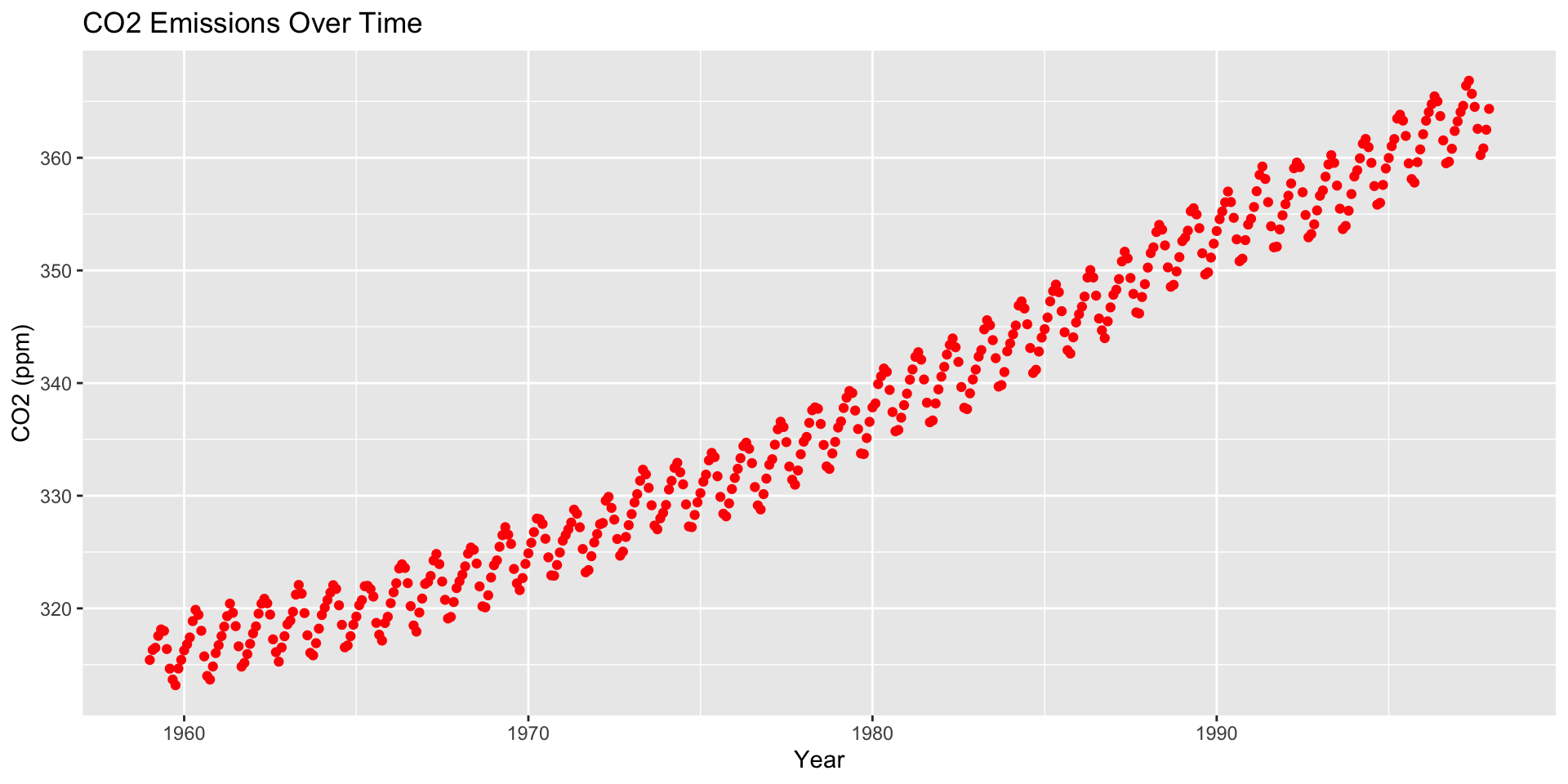
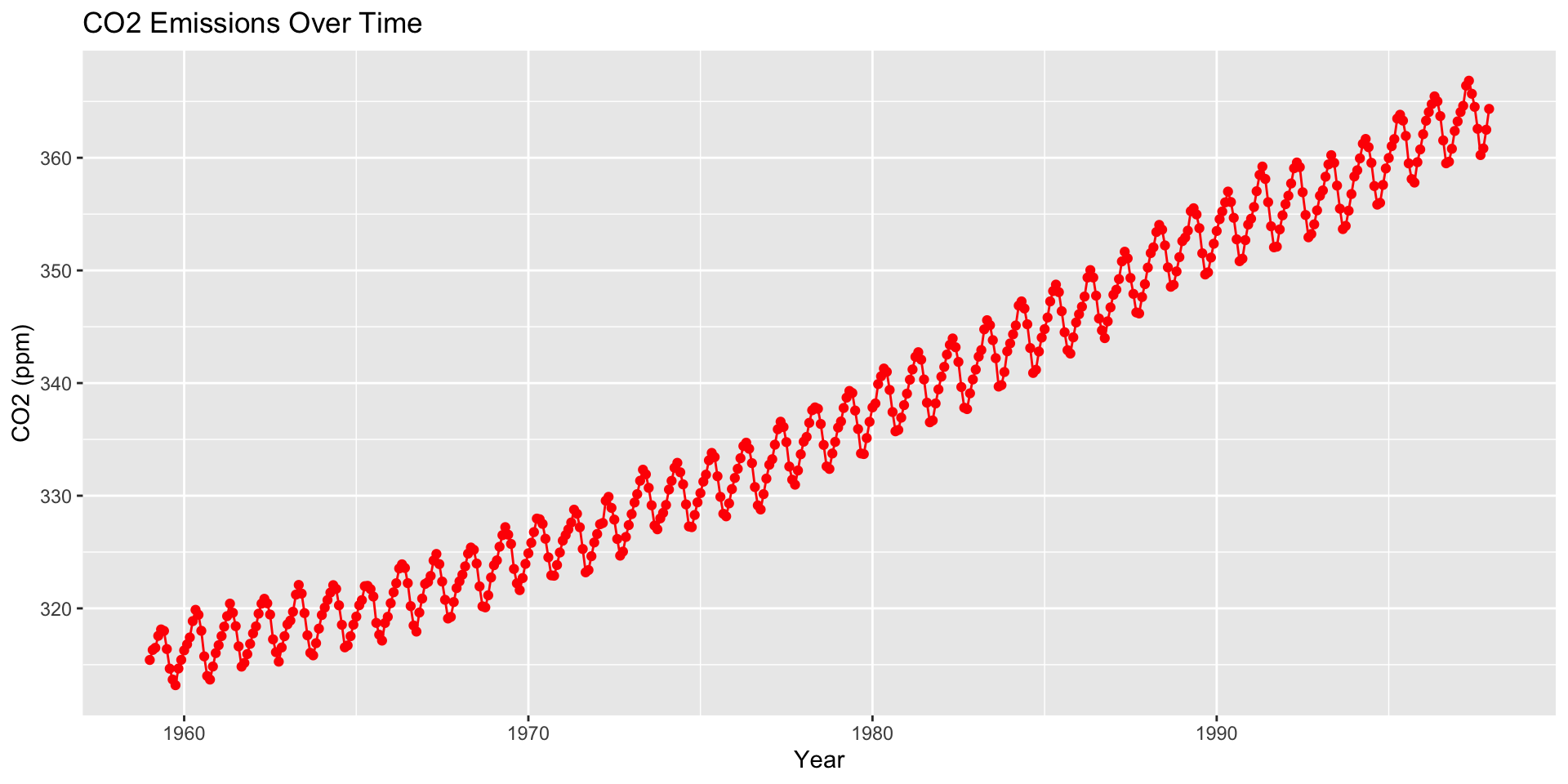
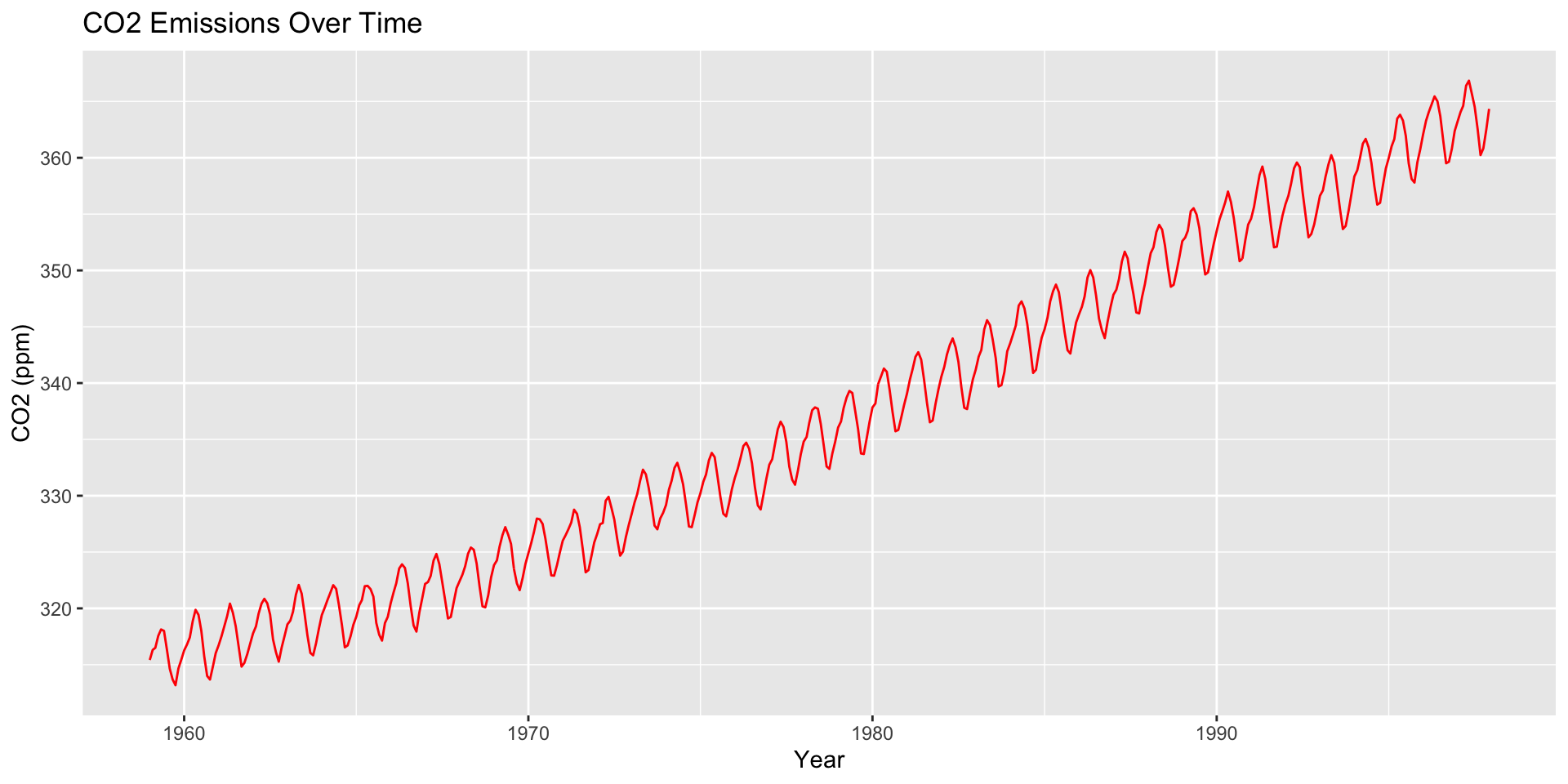
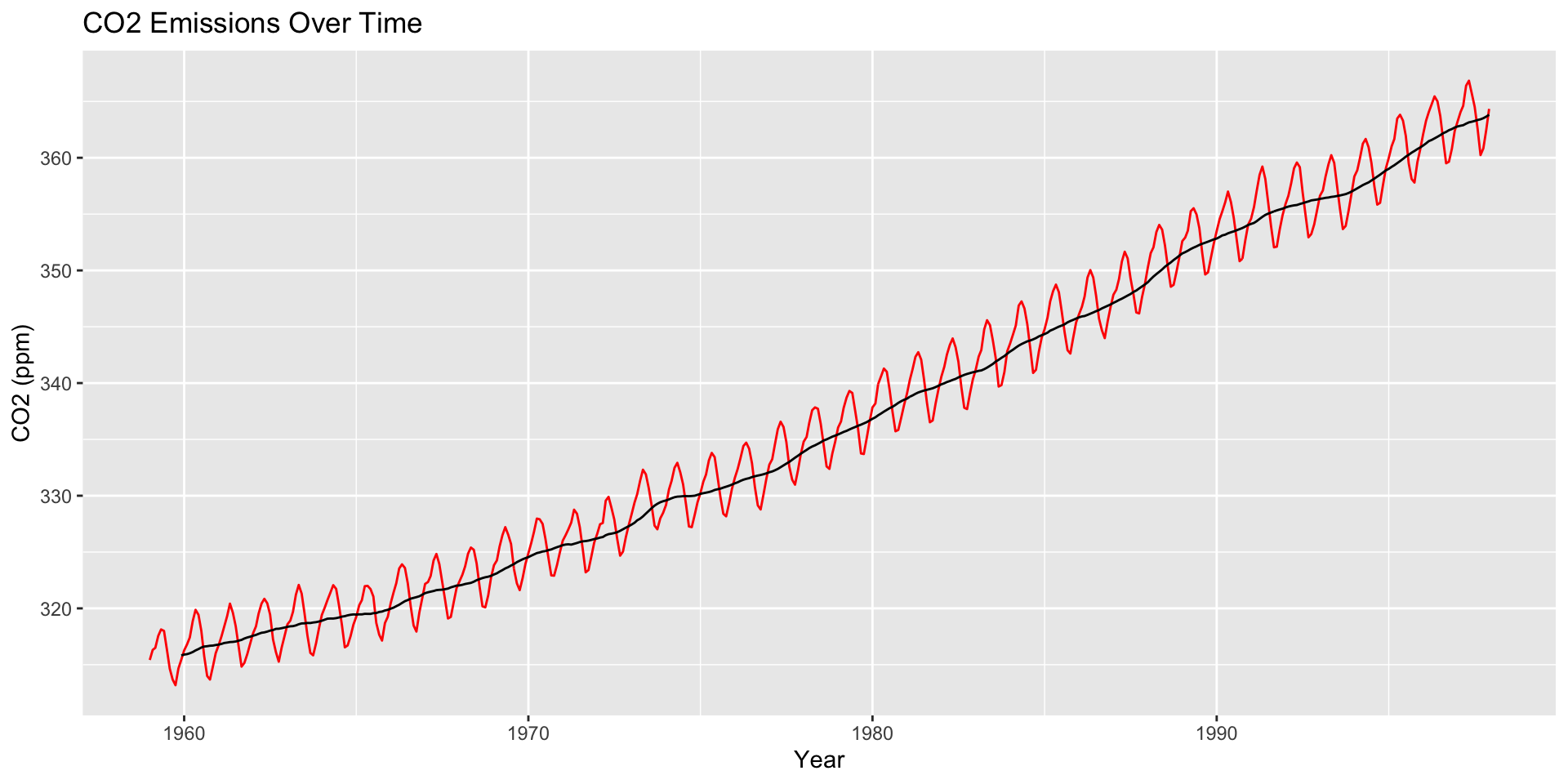
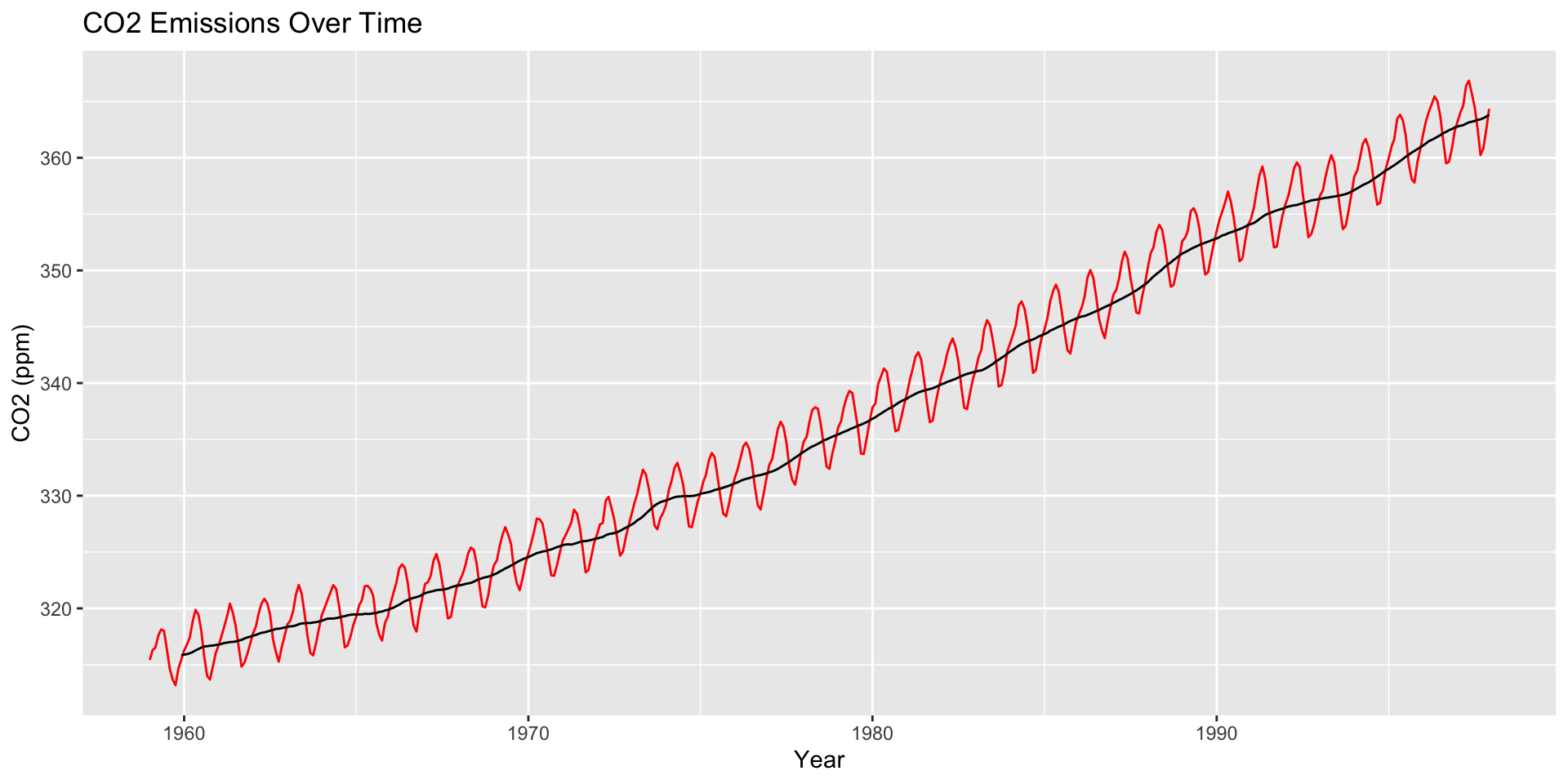
How are moving averages computed?
Intuition
Divide your data into small subsets (windows)
Compute the average within each window
Connect the averages together to make a trend line
Mathematically, a moving average can be written as the following:
\[\mu_k = \frac{\sum_{t=k - h + 1}^k X_t}{h}\]
Large \(h\): Smooth line; captures global trends
Small \(h\): Jagged/volatile line; captures local trends
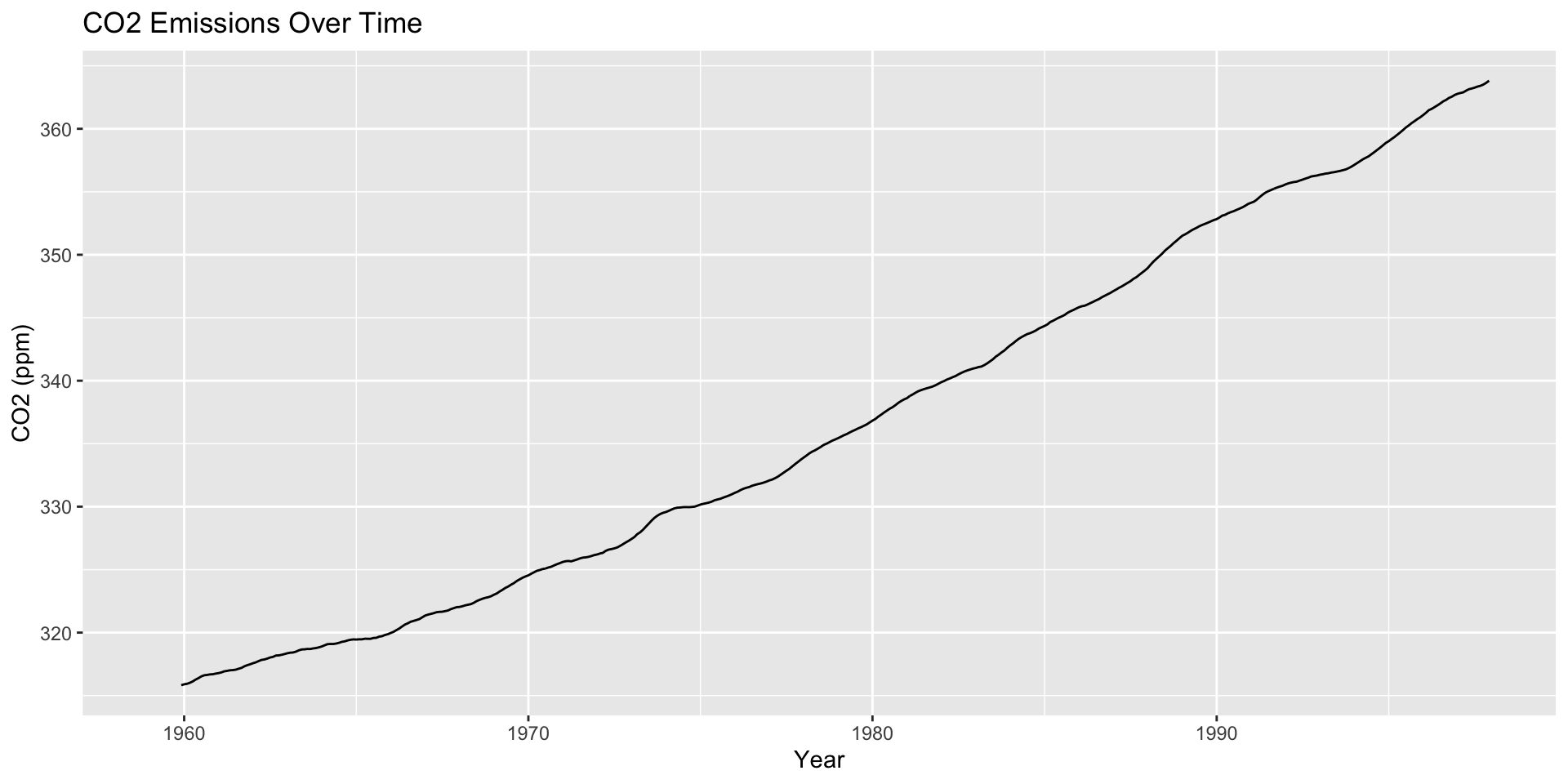
Working with Time Series
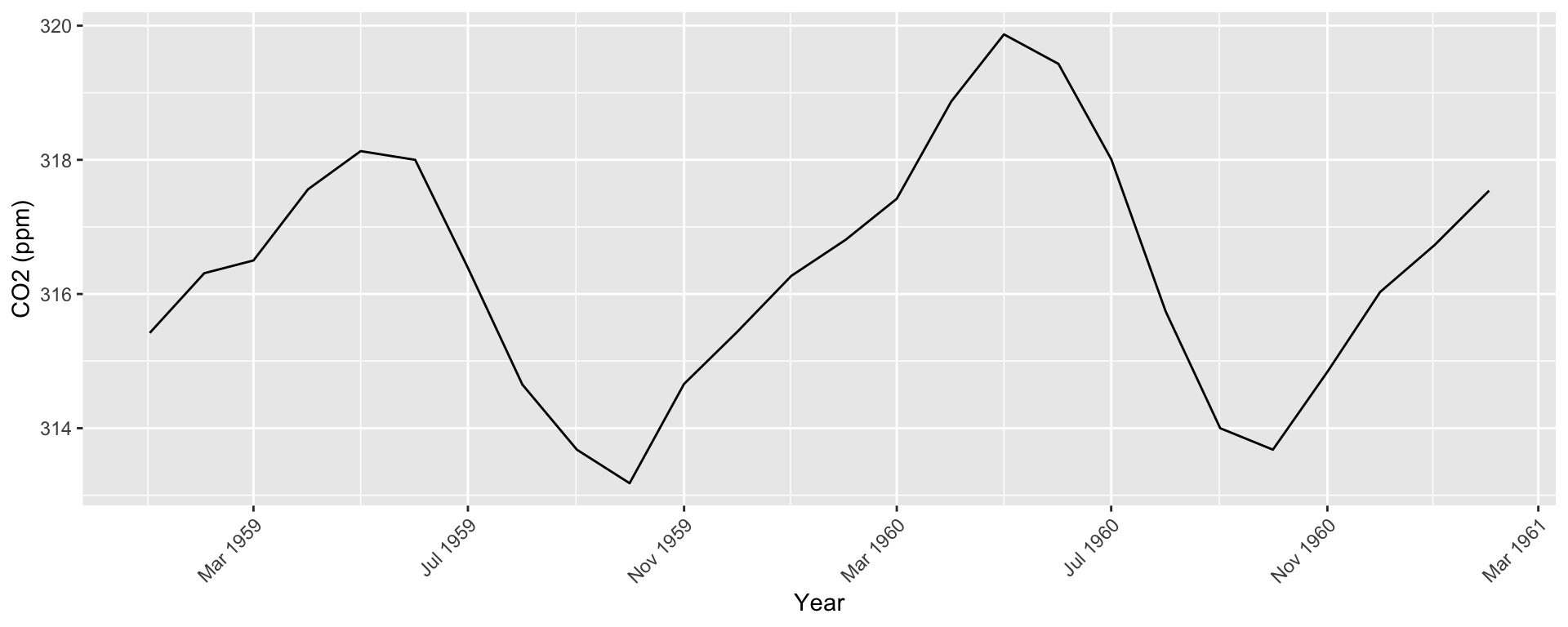
co2: Mauna Loa Atmospheric CO2 Concentration dataset (monthly \(\text{CO}^2\) concentration 1959 to 1997)
Formatting Dates
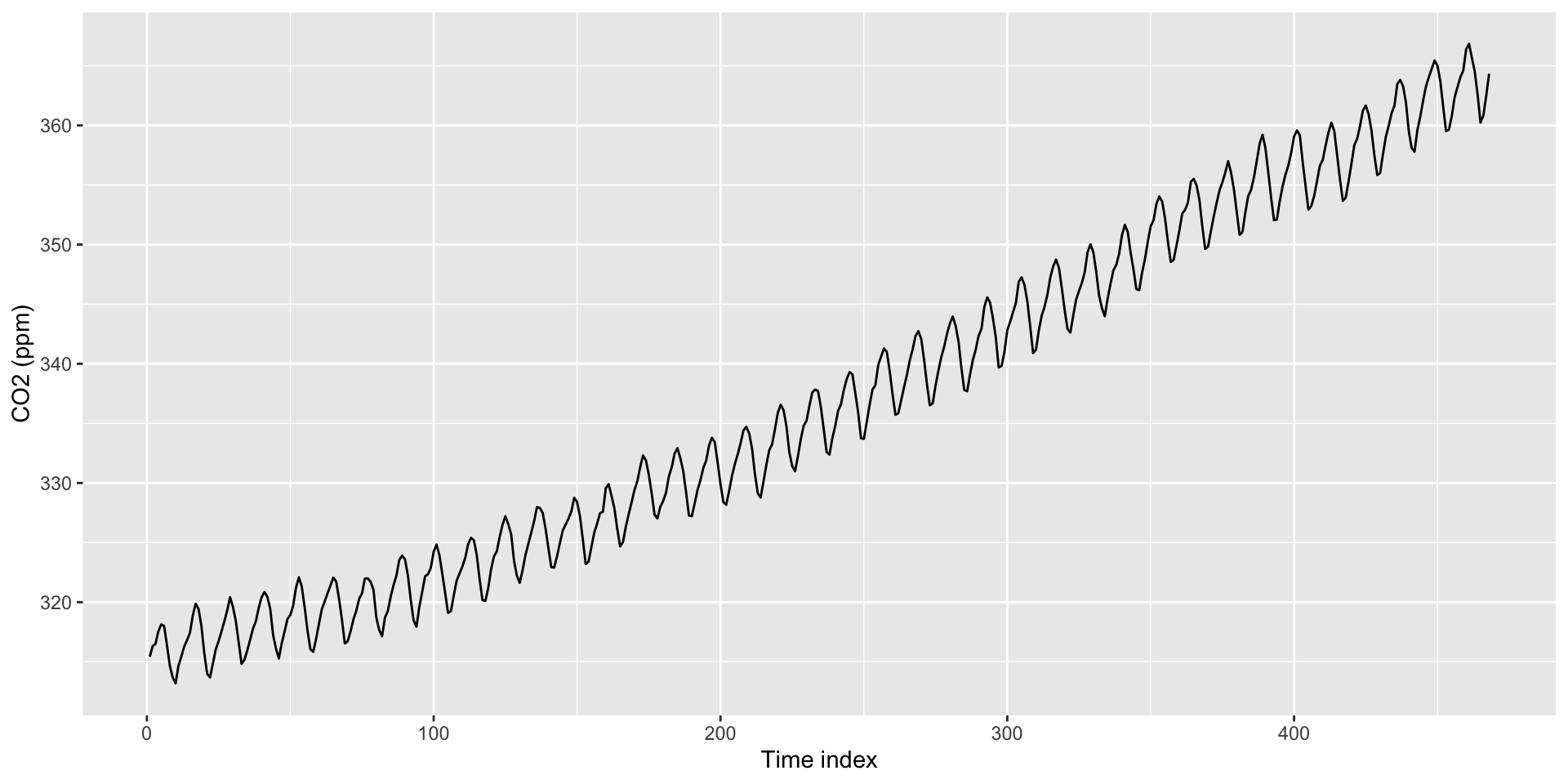
Can use as.Date() to create time indexes.
Default format is Year/Month/Day. For something else, need to specify format in as.Date() (e.g., format = "%m/%d/%Y")
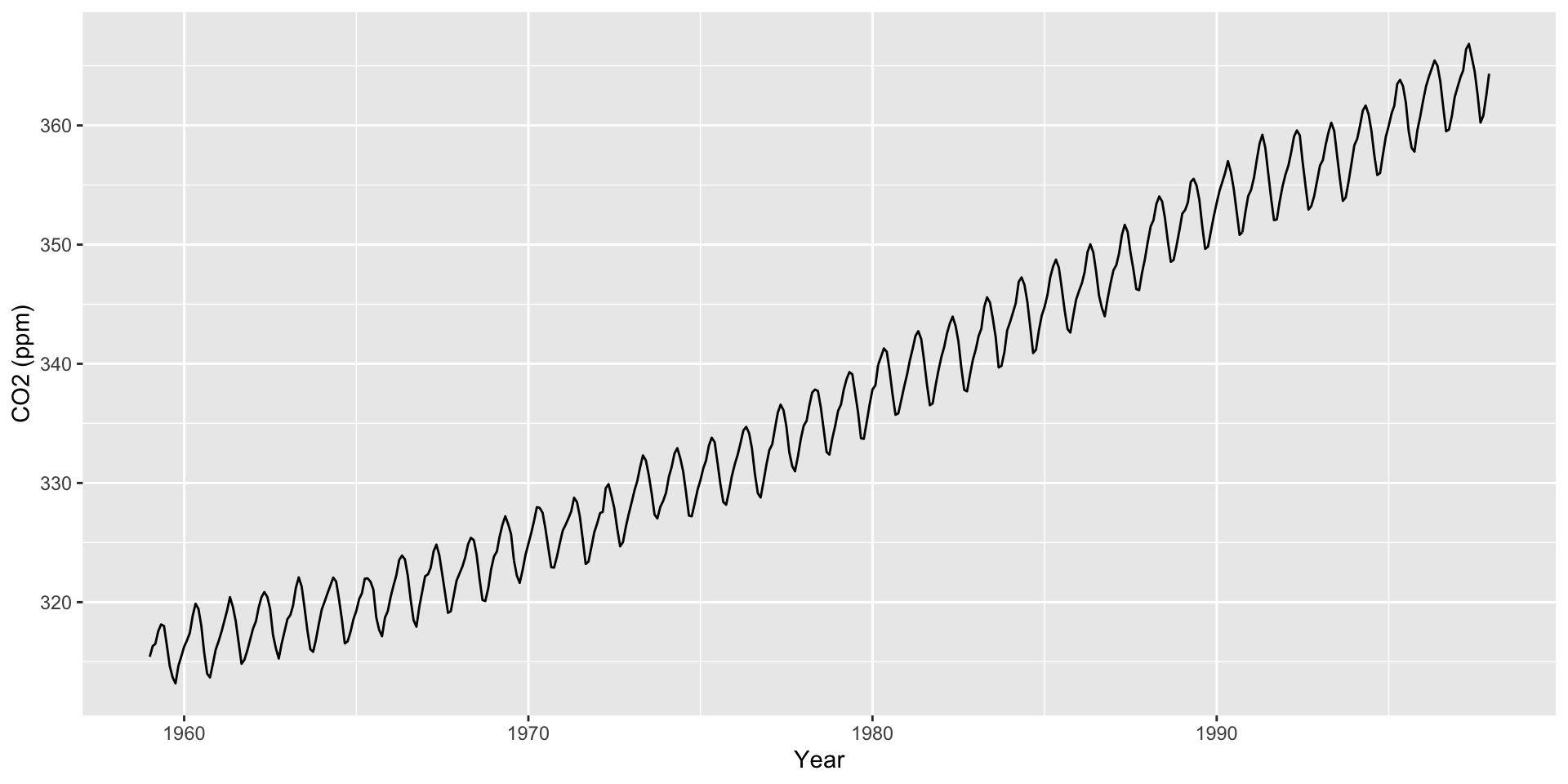
Use scale_x_date() to create interpretable axis labels
Use ggseas package to plot moving averages
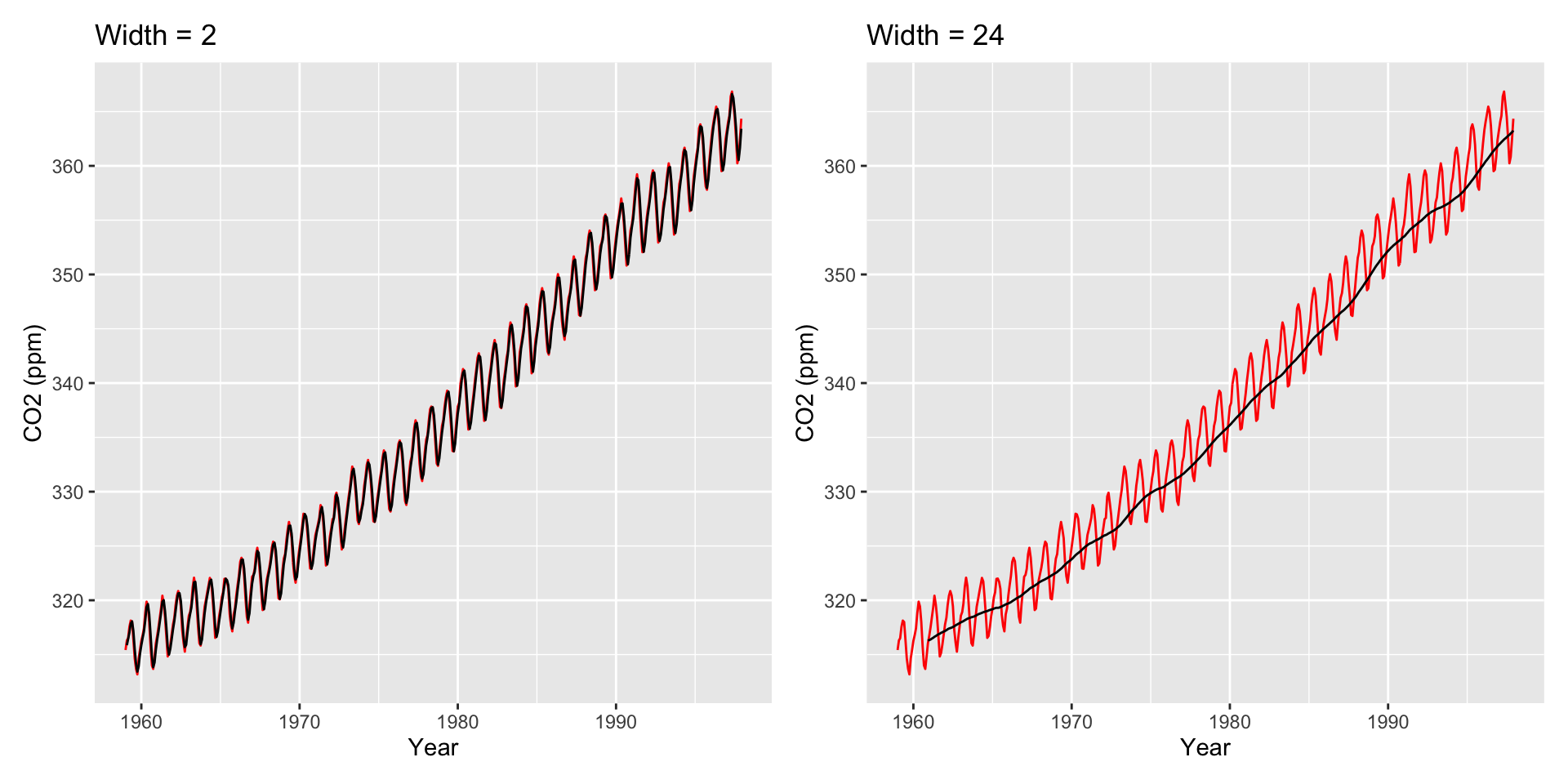
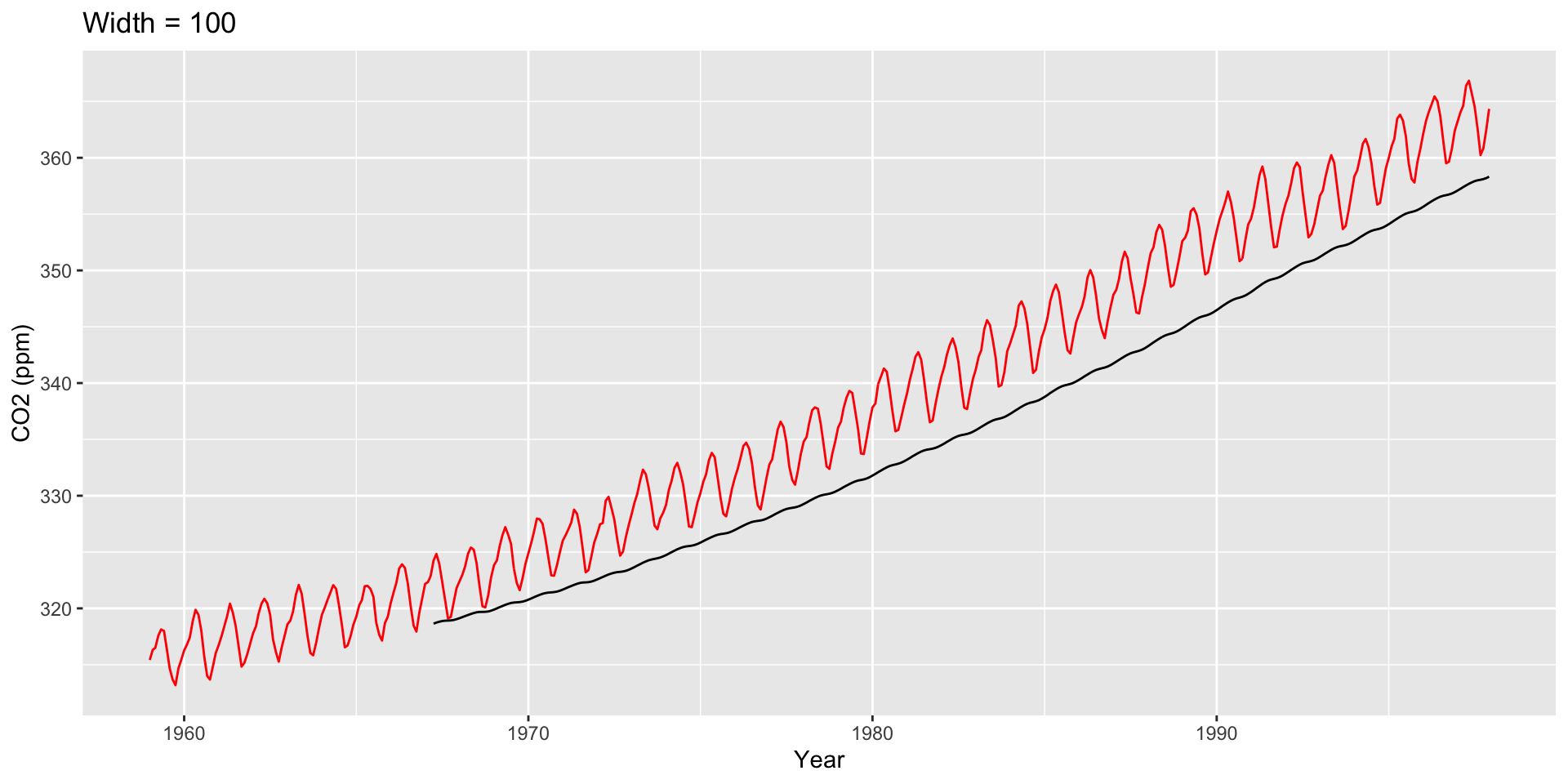
Other Moving Averages
Two other common averages: Cumulative moving averages and weighted moving averages.
- Cumulative moving average: The average at time \(k\) is the average of all points at and before \(k\). Mathematically:
\[\mu_k^{(CMA)} = \frac{\sum_{t=1}^k X_t}{k}\]
- Weighted moving average: Same as simple moving average, but different measurements get different weights for the average.
\[\mu_k^{(WMA)} = \frac{\sum_{t=k - h + 1}^k X_t \cdot w_t}{ \sum_{t=k - h + 1}^k w_t}\]
Working with lags
Time series data is fundamentally different from other data problems we’ve worked with because measurements are not independent
Obvious example: The temperature today is correlated with temperature yesterday. (Maybe not in Pittsburgh?)
Important term: lags. Used to determine if one time point influences future time points.
Lag 1: Comparing time series at time \(t\) with time series at time \(t - 1\).
Lag 2: Comparing time series at time \(t\) with time series at time \(t - 2\).
And so on…
Let’s say we have time measurements \((X_1, X_2, X_3, X_4, X_5)\).
The \(\ell = 1\) lag is \((X_2, X_3, X_4, X_5)\) vs \((X_1, X_2, X_3, X_4)\).
The \(\ell = 2\) lag is \((X_3, X_4, X_5)\) vs \((X_1, X_2, X_3)\).
Consider: Are previous outcomes (lags) predictive of future outcomes?
Autocorrelation
Autocorrelation: Correlation between a time series and a lagged version of itself.
Define \(r_{\ell}\) as the correlation between a time series and Lag \(\ell\) of that time series.
Lag 1: \(r_1\) is correlation between \((X_2, X_3, X_4, X_5)\) and \((X_1,X_2,X_3,X_4)\)
Lag 2: \(r_2\) is correlation between \((X_3, X_4, X_5)\) and \((X_1,X_2,X_3)\)
And so on…
Common diagnostic: Plot \(\ell\) on x-axis, \(r_{\ell}\) on y-axis.
Tells us if correlations are “significantly large” or “significantly small” for certain lags
To make an autocorrelation plot, we use the acf() function; the ggplot version uses autoplot()
Autocorrelation plots
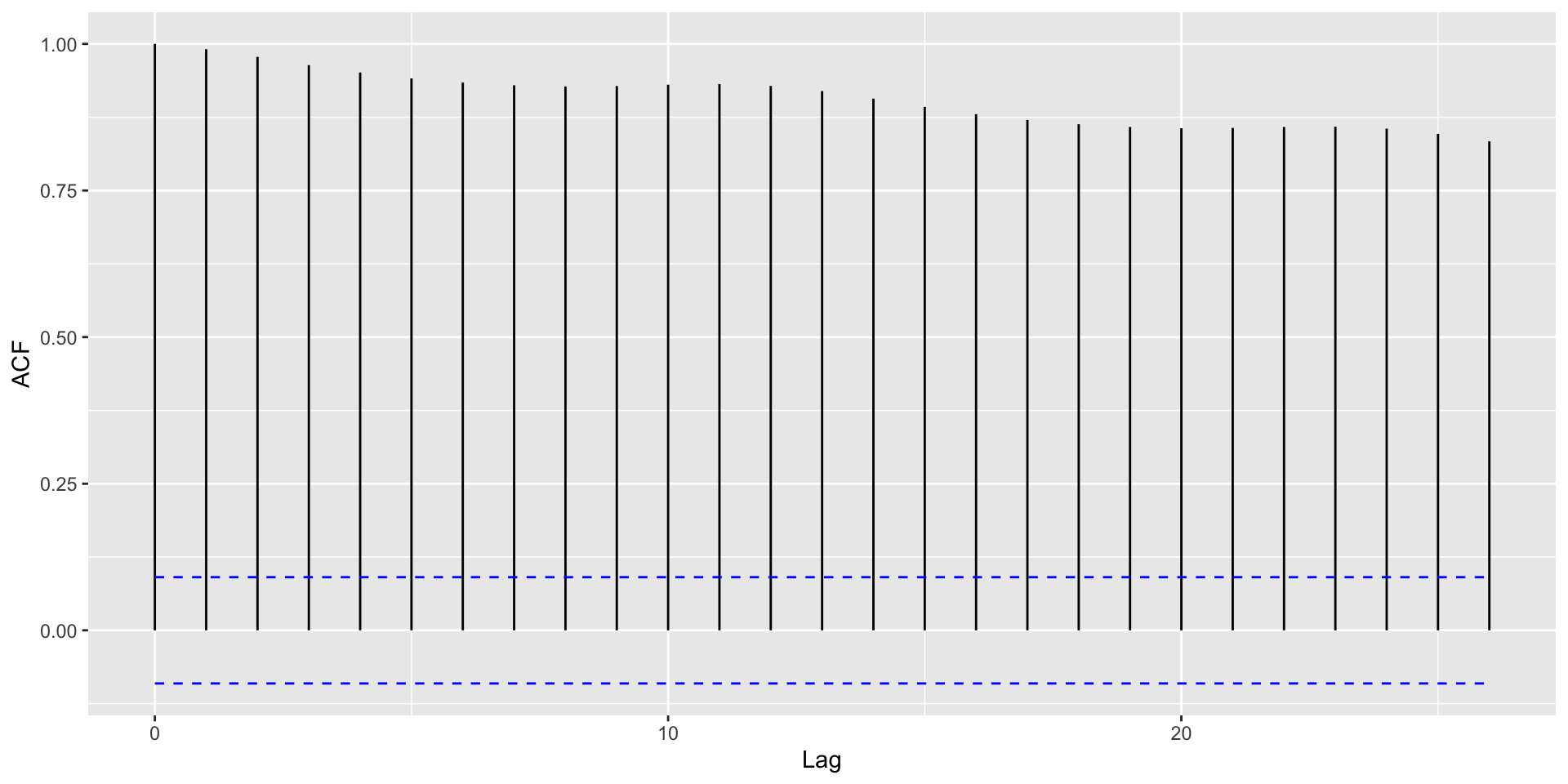
Autocorrelation Plots and Seasonality
With strong global trends, autocorrelations will be very positive.
. . .
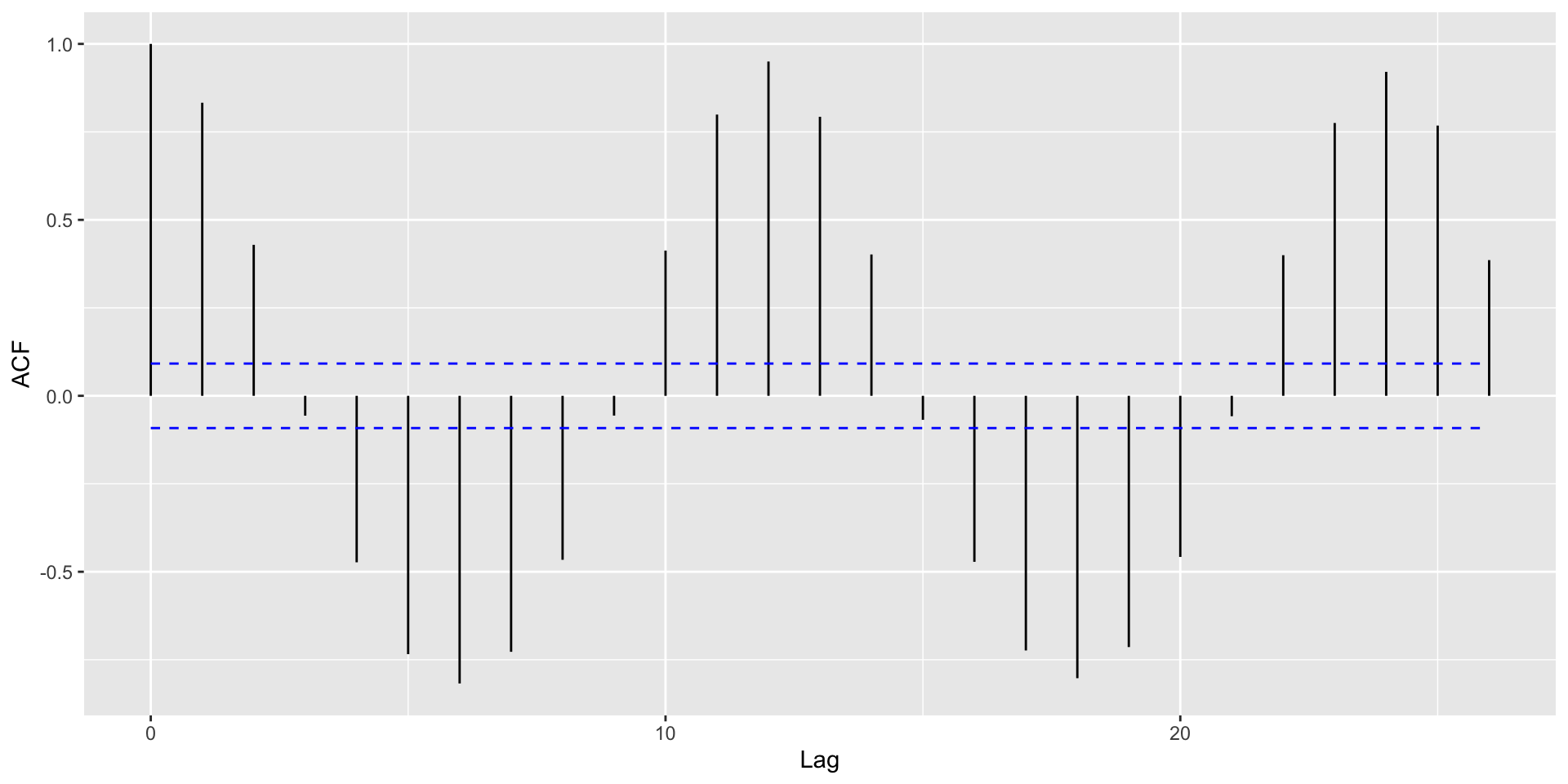
Helpful: Visualize autocorrelations after removing the global trend (compute moving average with rollapply())
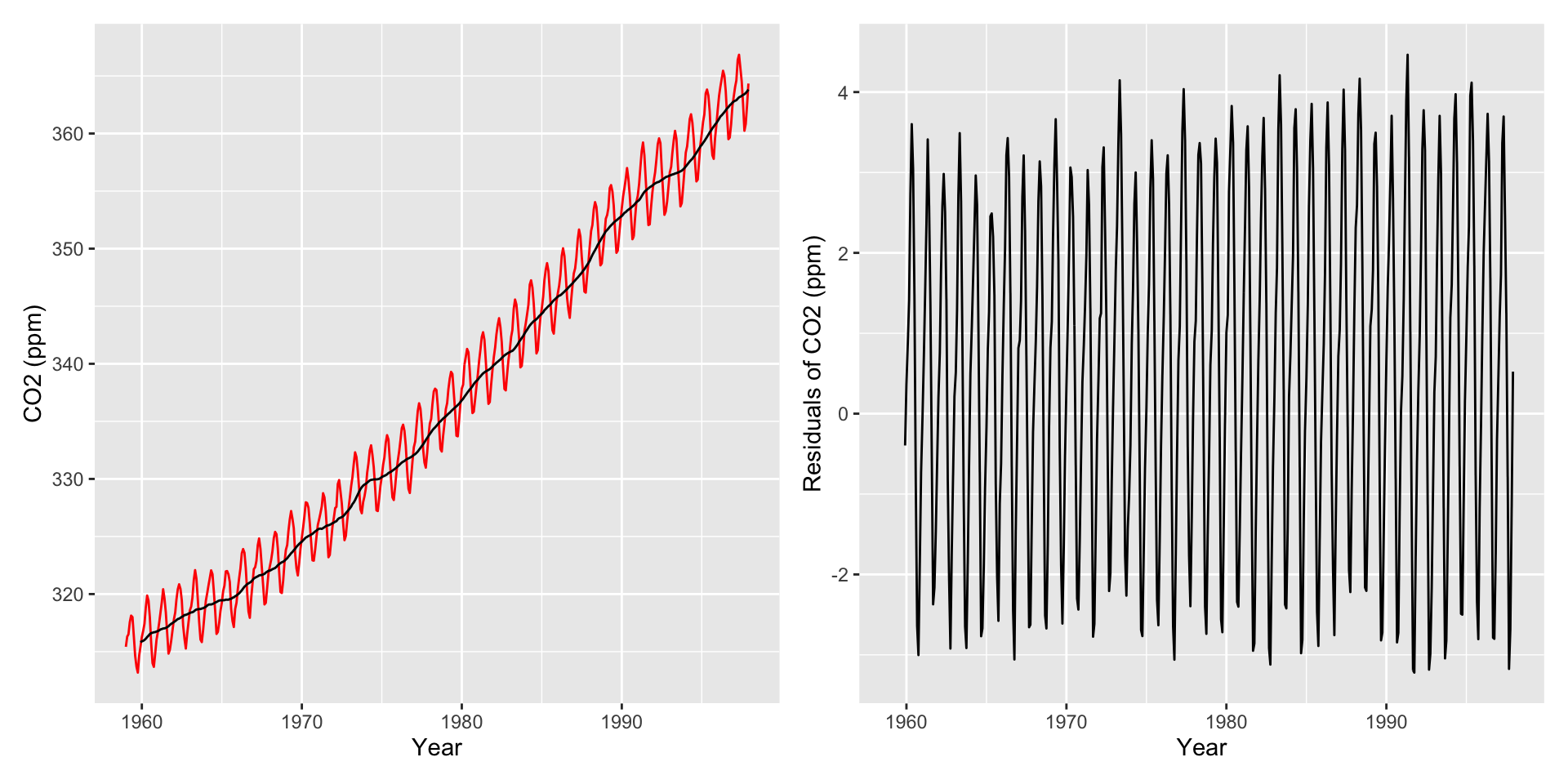
Autocorrelation Plots and Seasonality
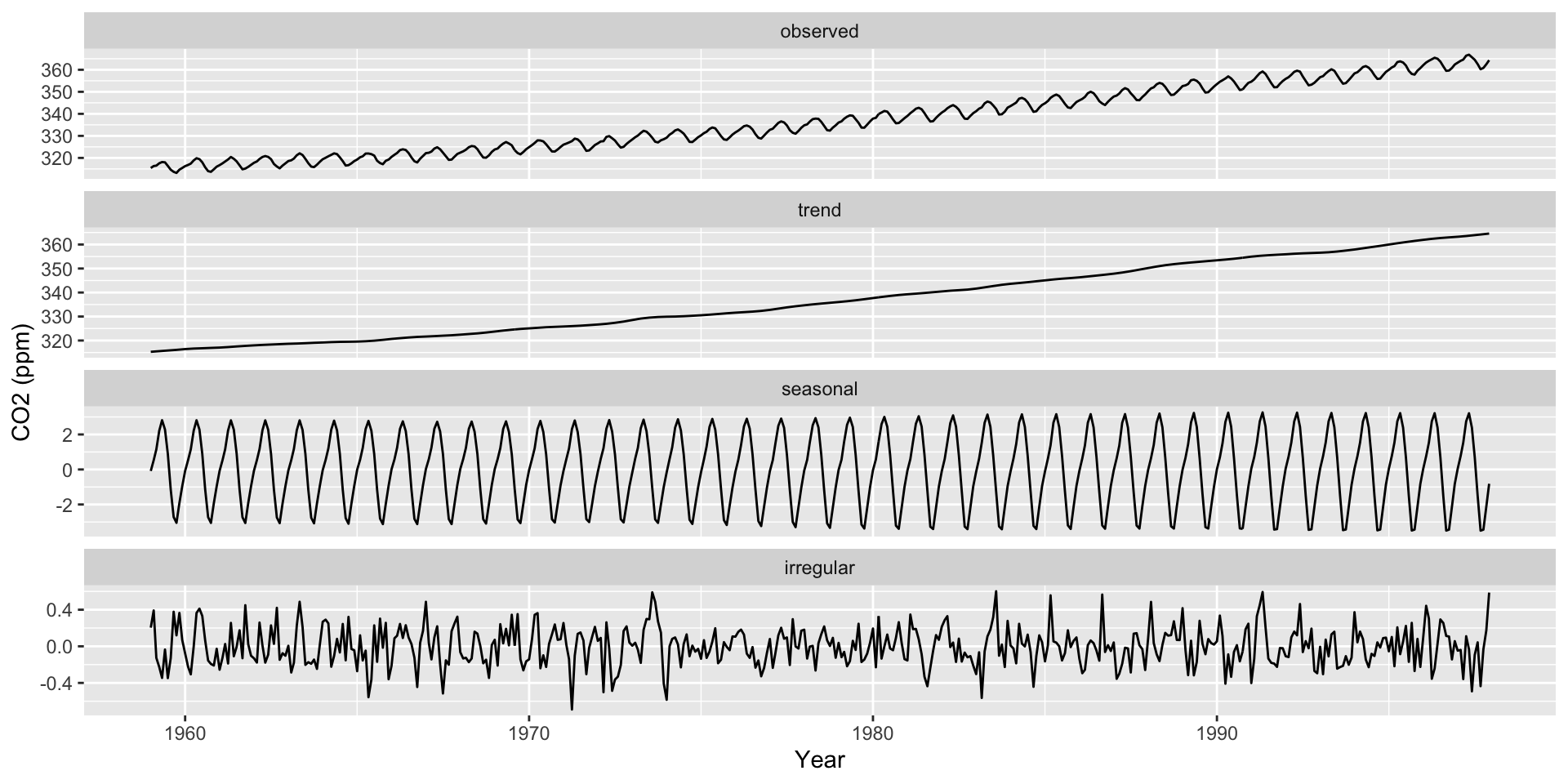
Seasonality Decomposition
Remember that there are three main components to a time series:
Average trends
Seasonality
Noise
. . .
Use ggsdc() (from ggseas) to decompose a time series into these three components
Plots the observed time series.
Plots a loess curve as the global trend.
Plots another loess curve on (observed - trend) as the seasonality.
Plots the noise (observed - trend - seasonality).
Seasonality Decomposition
Recap and next steps
Discussed non-linear dimension reduction with t-SNE plots
Discussed various aspects of visualizing trends
Walked through basics of time series data, such as moving averages, autocorrelation, seasonality
HW4 is due Wednesday Sept 25th
You need to email me a draft of your EDA report! (1 per group)
Next time: Visualizing spatial data
Recommended reading: How to Use t-SNE Effectively, Understanding UMAP, CW CH 13 Visualizing time series and other functions of an independent variable, CW CH 14 Visualizing trends