Time series and intro to spatial data

Prof Ron Yurko

2024-09-25

Reminders, previously, and today…

  • HW4 is due TONIGHT Sept 25th

  • You need to email me a draft of your EDA report! (1 per group)

  • Walked through non-linear dimension reduction with t-SNE

  • Discussed visualizing trends, highglighting points of emphasis

TODAY:

  • Walk through the basics of time series data techniques

  • Introduce visualizations and inference with spatial data

Things of interest for time series data

Time series can be characterized by three features:

  1. Trends: Does the variable increase or decrease over time, on average?

  2. Seasonality: Are there changes in the variable that regularly happen (e.g., every winter, every hour, etc.)? Sometimes called periodicity.

  3. Noise: Variation in the variable beyond average trends and seasonality.

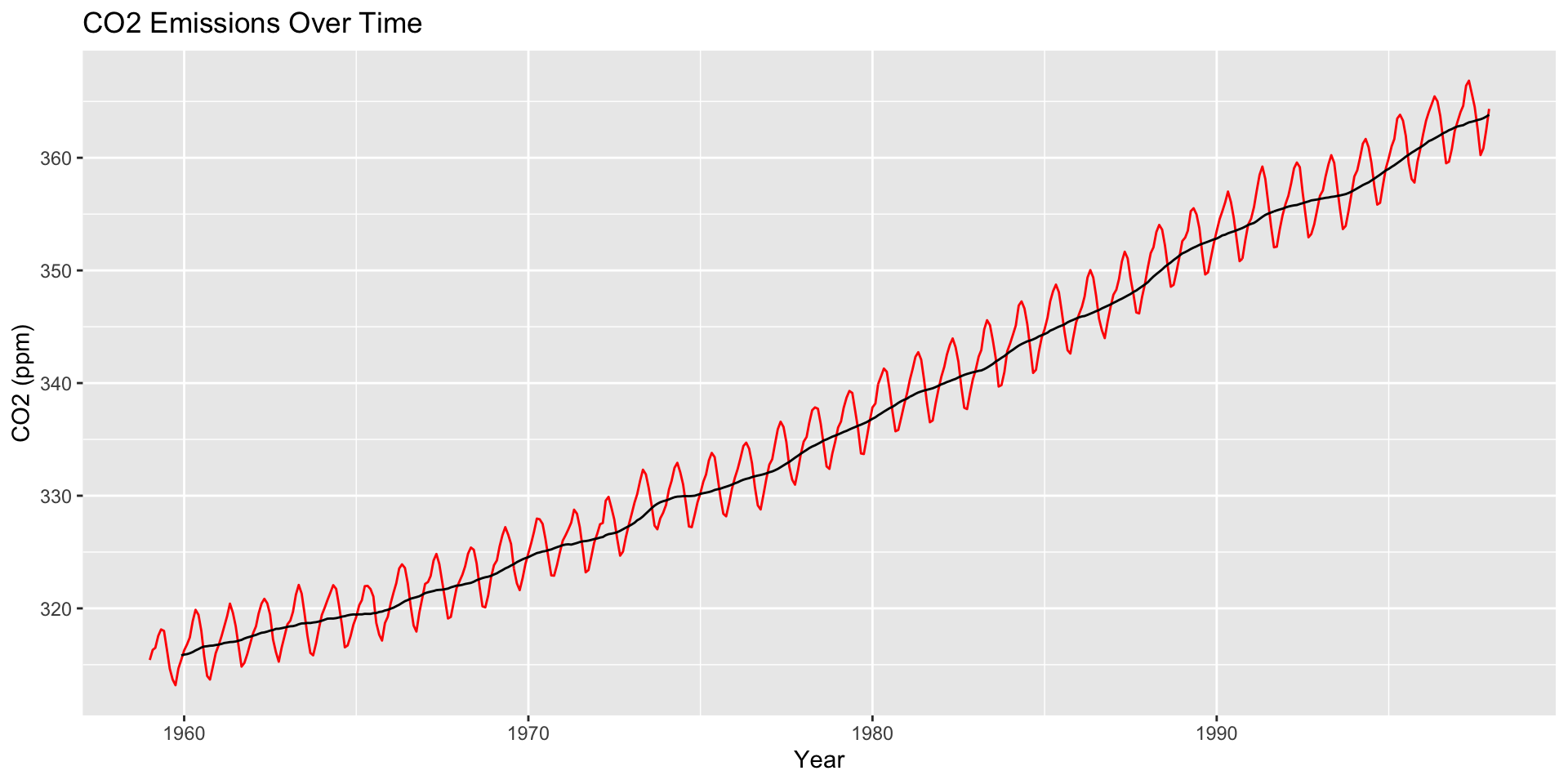
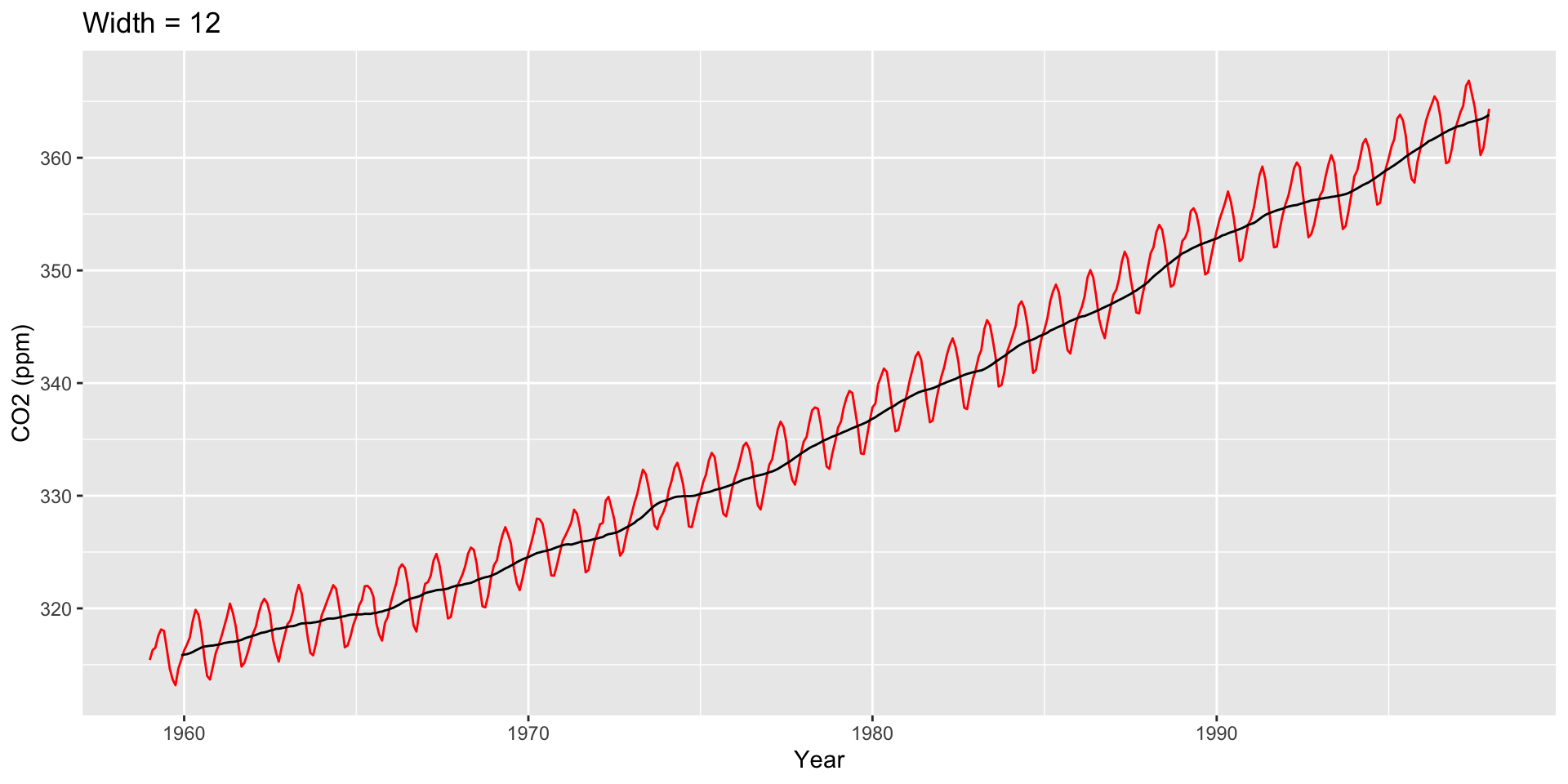
Moving averages are a starting point for visualizing how a trend changes over time

Be responsible with your axes!

Be responsible with your axes!

Moving Average Plots

The Financial Times COVID-19 plots displayed a moving average (sometimes called a rolling average)

Intuition

  1. Divide your data into small subsets (“windows”)

  2. Compute the average within each window

  3. Connect the averages together to make a trend line

Sometimes called a simple moving average

This is exactly what we did with LOESS… we called this a sliding window, but it’s the same thing

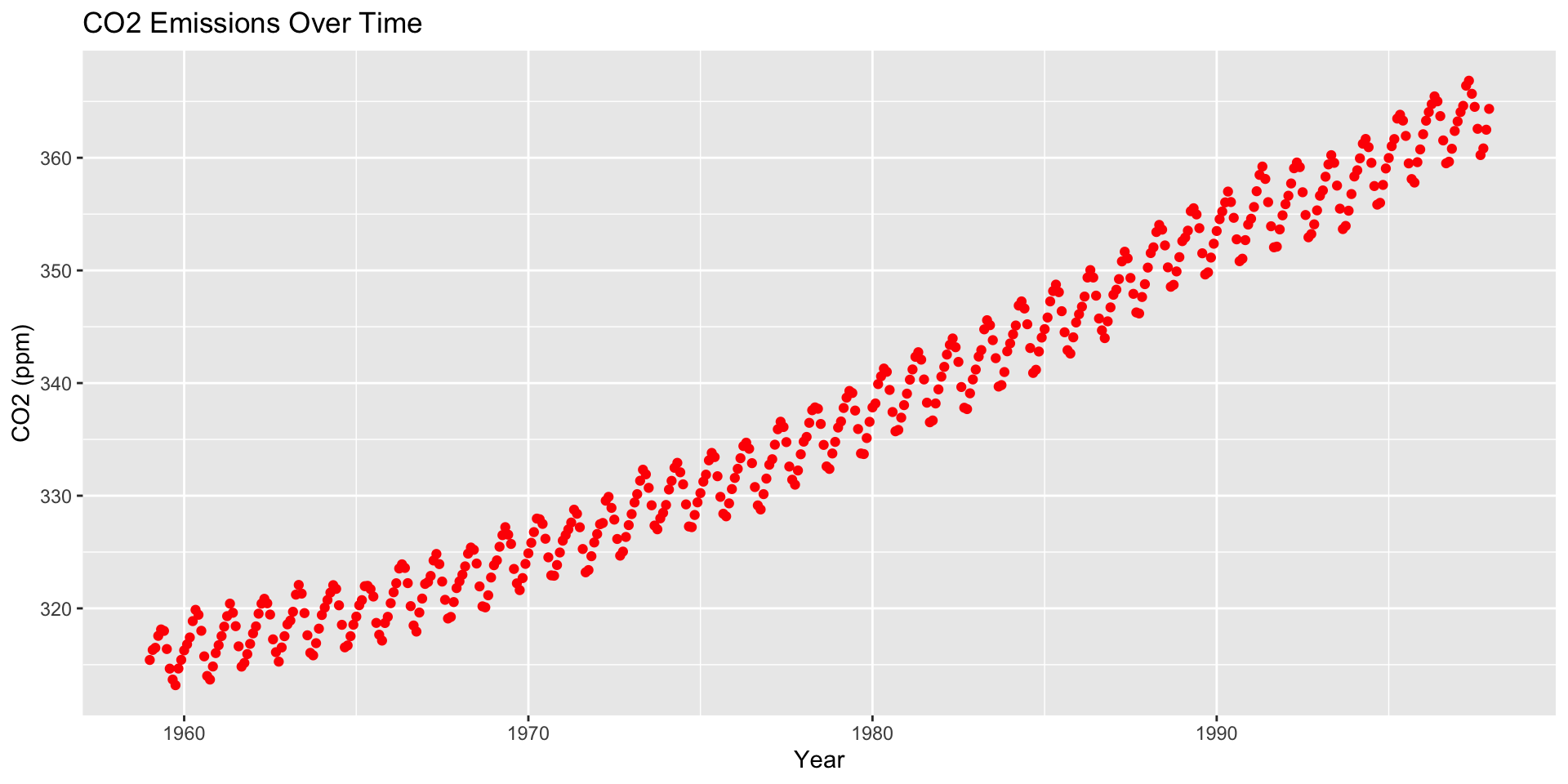
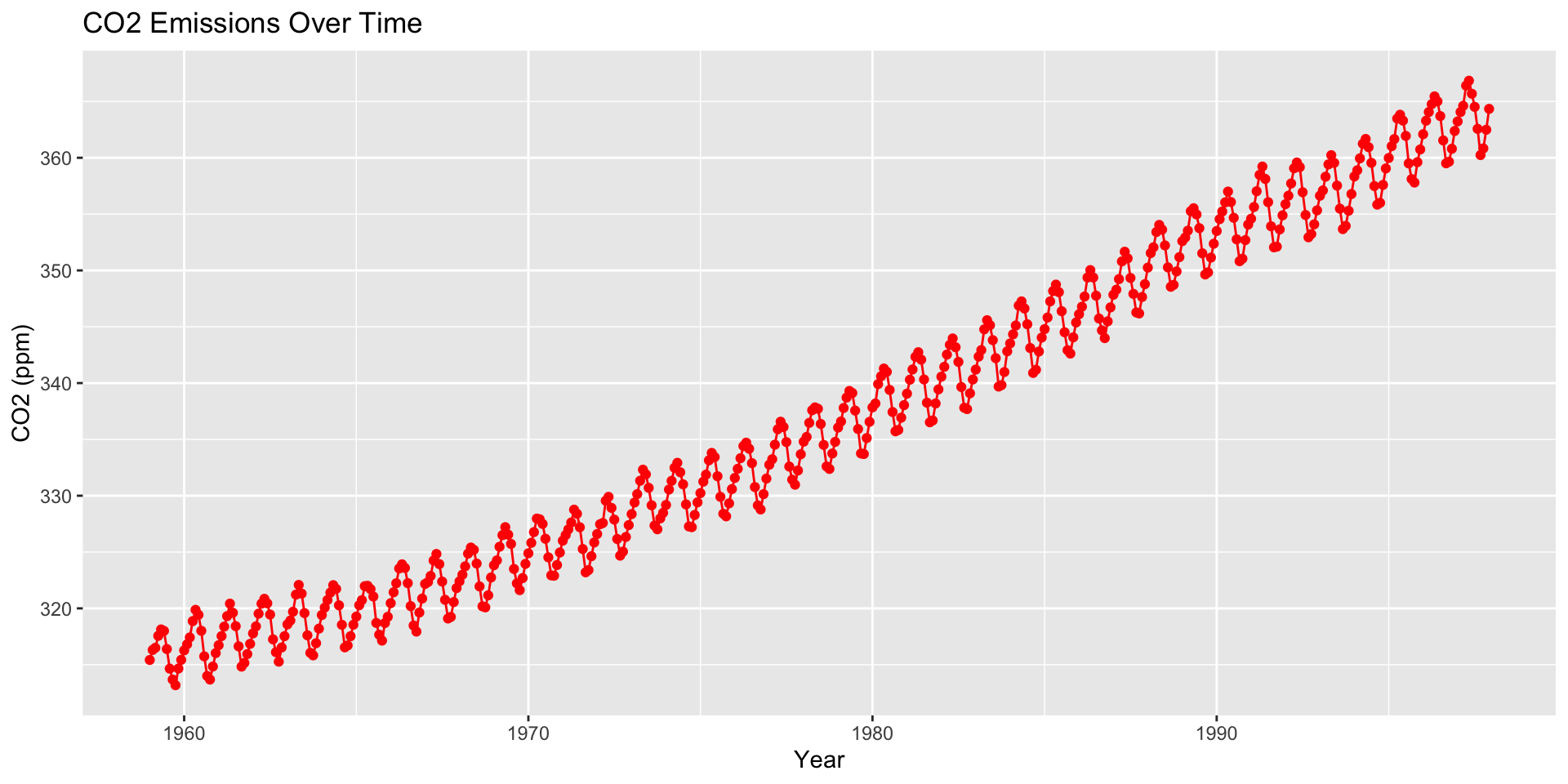
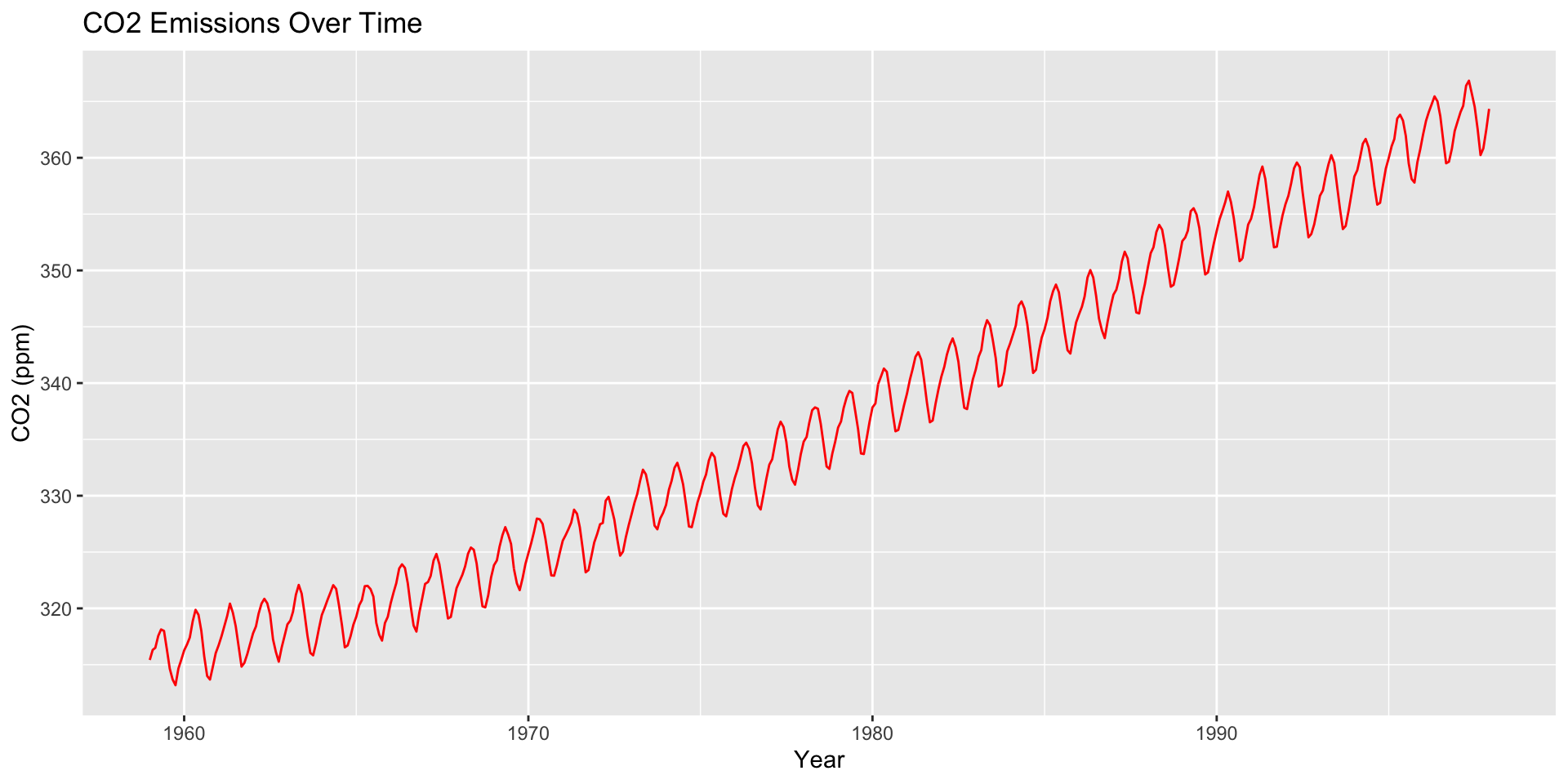
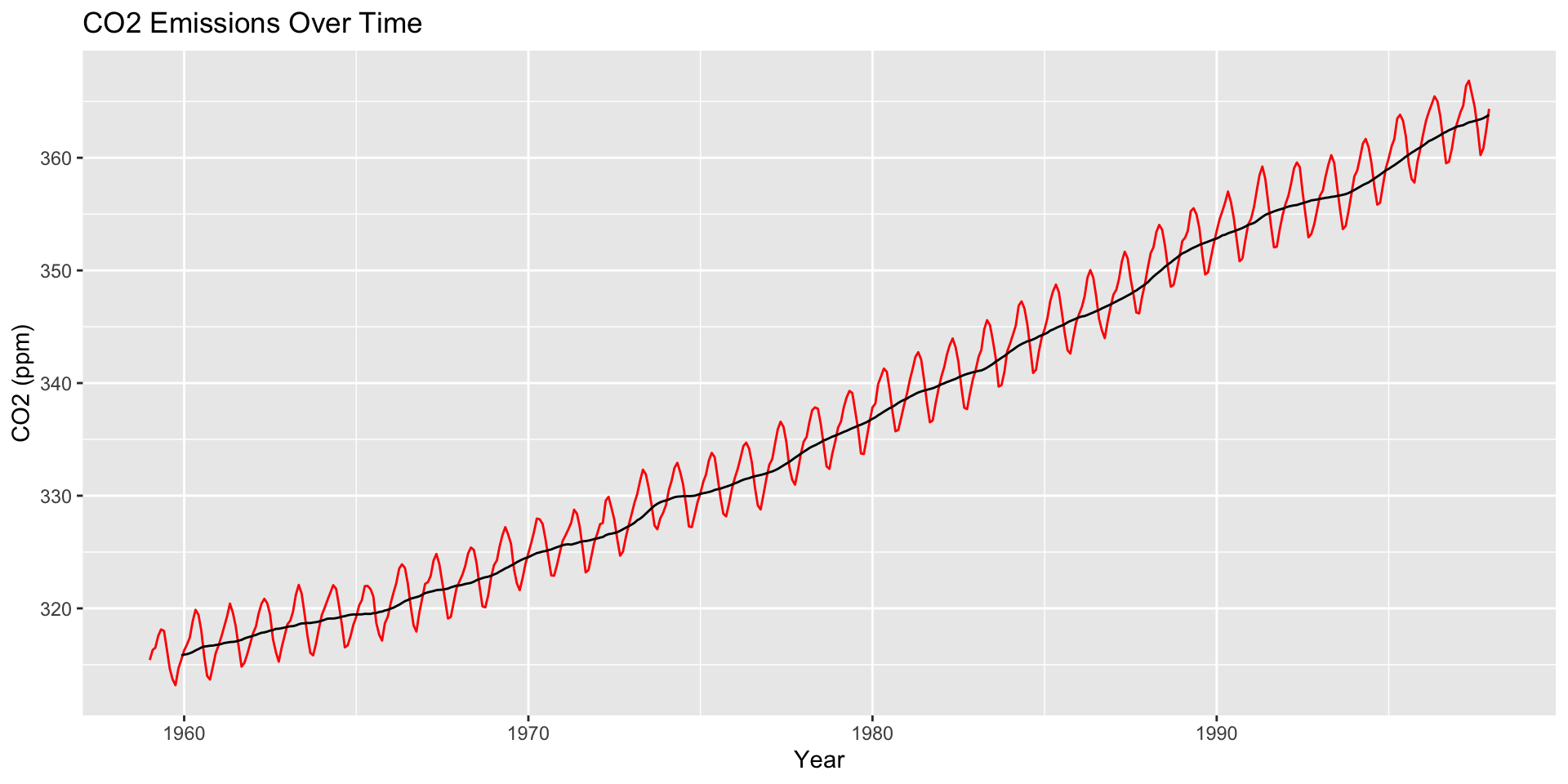
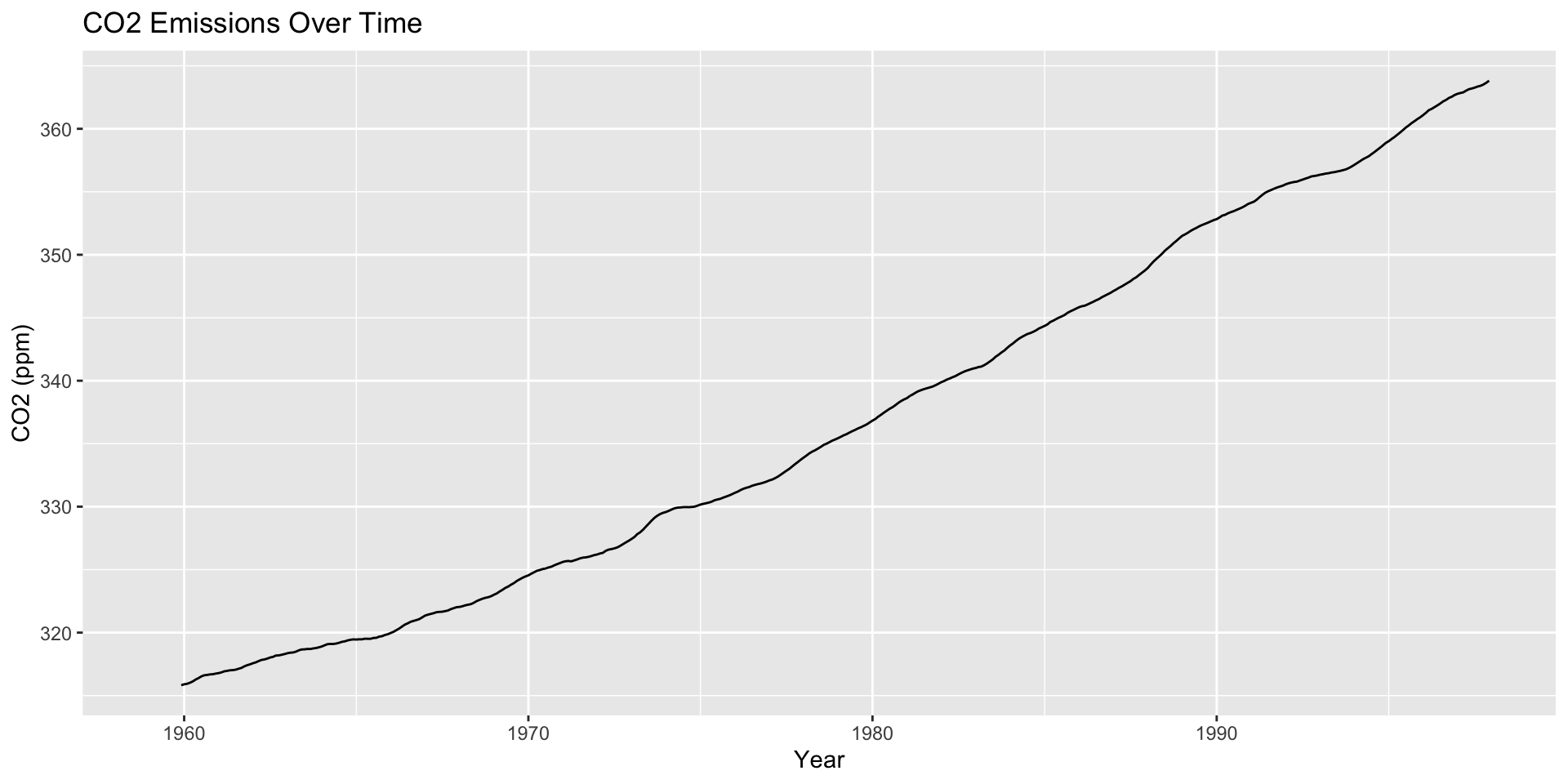
How are moving averages computed?

Intuition

  1. Divide your data into small subsets (windows)

  2. Compute the average within each window

  3. Connect the averages together to make a trend line

Mathematically, a moving average can be written as the following:

\[\mu_k = \frac{\sum_{t=k - h + 1}^k X_t}{h}\]

  • Large \(h\): Smooth line; captures global trends

  • Small \(h\): Jagged/volatile line; captures local trends

Working with Time Series

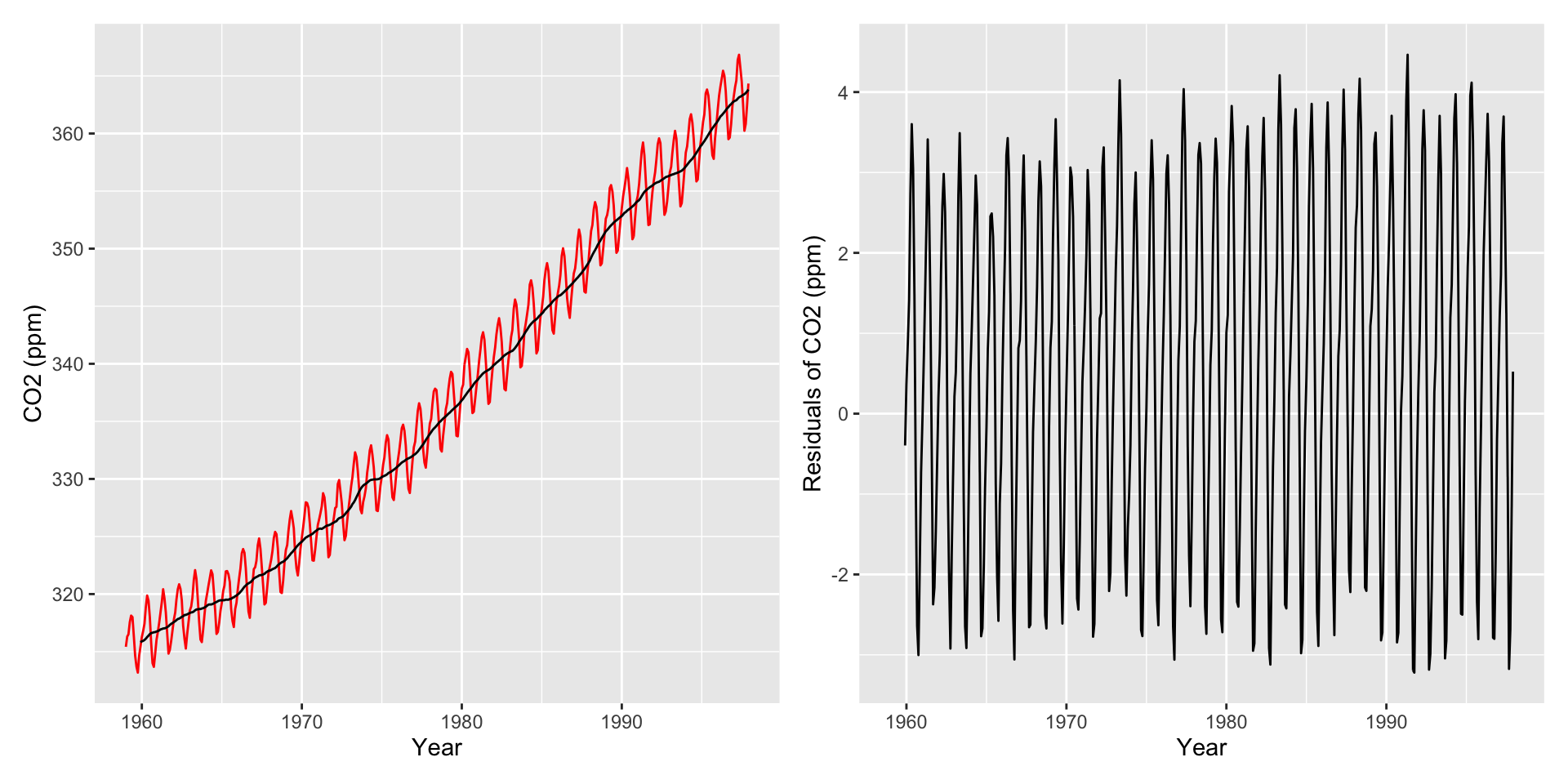
co2: Mauna Loa Atmospheric CO2 Concentration dataset (monthly \(\text{CO}^2\) concentration 1959 to 1997)

co2_tbl |>
  ggplot(aes(x = obs_i, y = co2_val)) + 
  geom_line() + 
  labs(x = "Time index", y = "CO2 (ppm)")

Formatting Dates

Can use as.Date() to create time indexes.

Default format is Year/Month/Day. For something else, need to specify format in as.Date() (e.g., format = "%m/%d/%Y")

Use scale_x_date() to create interpretable axis labels

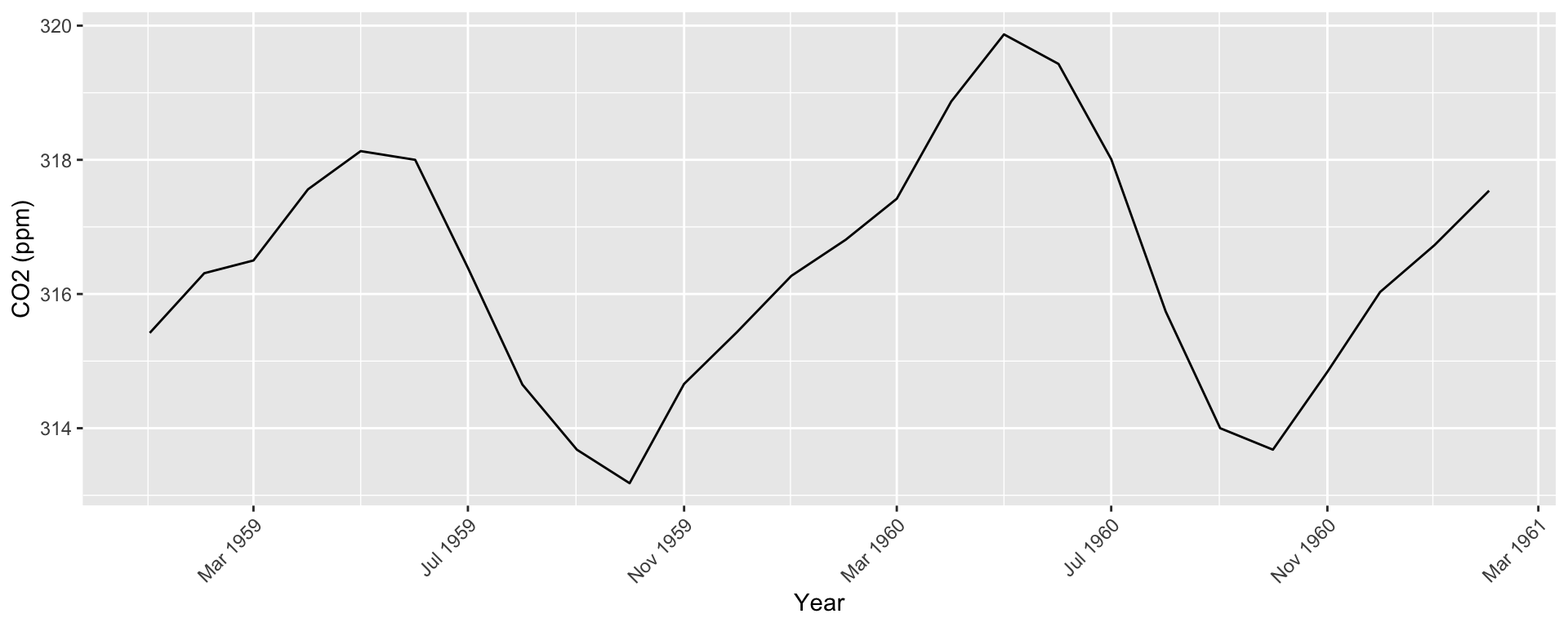
Use ggseas package to plot moving averages

library(ggseas)
co2_tbl |> 
  ggplot(aes(x = obs_date, y = co2_val)) + geom_line(color = "red") + 
  stat_rollapplyr(width = 12, align = "right") +
  labs(x = "Year", y = "CO2 (ppm)", title = "Width = 12")

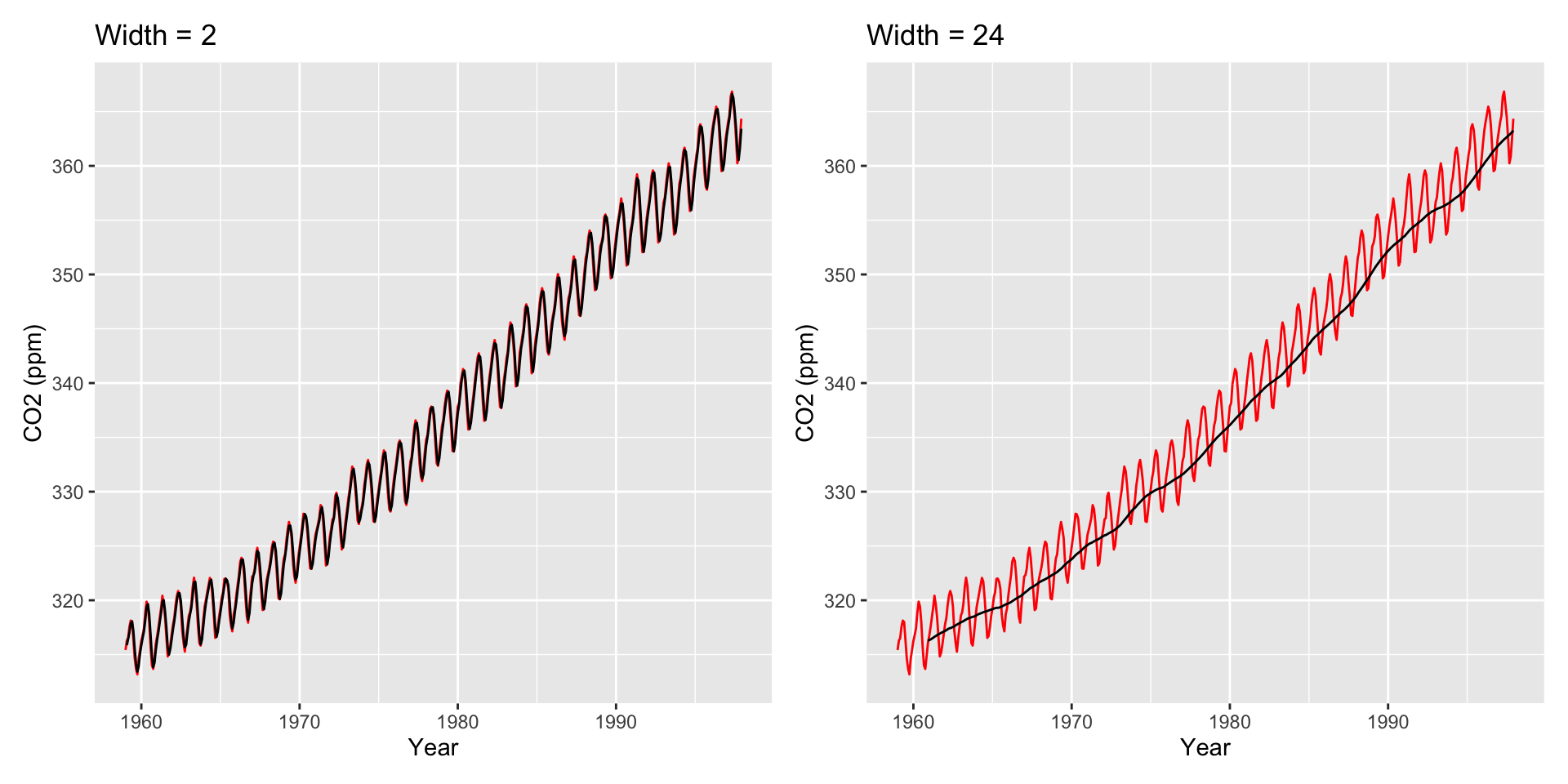
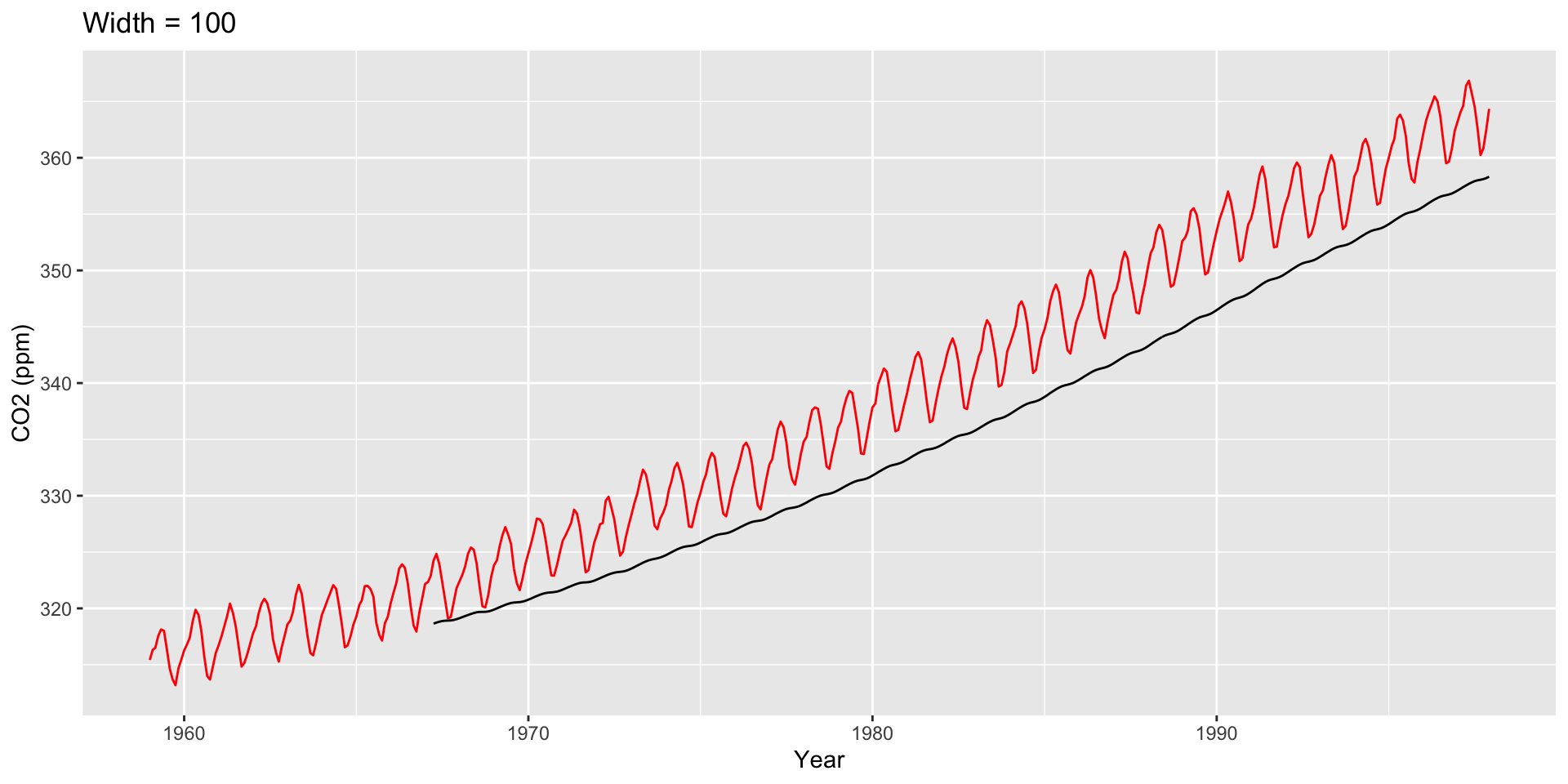
Other Moving Averages

Two other common averages: Cumulative moving averages and weighted moving averages.

  • Cumulative moving average: The average at time \(k\) is the average of all points at and before \(k\). Mathematically:

\[\mu_k^{(CMA)} = \frac{\sum_{t=1}^k X_t}{k}\]

  • Weighted moving average: Same as simple moving average, but different measurements get different weights for the average.

\[\mu_k^{(WMA)} = \frac{\sum_{t=k - h + 1}^k X_t \cdot w_t}{ \sum_{t=k - h + 1}^k w_t}\]

Working with lags

Time series data is fundamentally different from other data problems we’ve worked with because measurements are not independent

Obvious example: The temperature today is correlated with temperature yesterday. (Maybe not in Pittsburgh?)

Important term: lags. Used to determine if one time point influences future time points.

Lag 1: Comparing time series at time \(t\) with time series at time \(t - 1\).

Lag 2: Comparing time series at time \(t\) with time series at time \(t - 2\).

And so on…

Let’s say we have time measurements \((X_1, X_2, X_3, X_4, X_5)\).

The \(\ell = 1\) lag is \((X_2, X_3, X_4, X_5)\) vs \((X_1, X_2, X_3, X_4)\).

The \(\ell = 2\) lag is \((X_3, X_4, X_5)\) vs \((X_1, X_2, X_3)\).

Consider: Are previous outcomes (lags) predictive of future outcomes?

Autocorrelation

Autocorrelation: Correlation between a time series and a lagged version of itself.

Define \(r_{\ell}\) as the correlation between a time series and Lag \(\ell\) of that time series.

Lag 1: \(r_1\) is correlation between \((X_2, X_3, X_4, X_5)\) and \((X_1,X_2,X_3,X_4)\)

Lag 2: \(r_2\) is correlation between \((X_3, X_4, X_5)\) and \((X_1,X_2,X_3)\)

And so on…

Common diagnostic: Plot \(\ell\) on x-axis, \(r_{\ell}\) on y-axis.

Tells us if correlations are “significantly large” or “significantly small” for certain lags

To make an autocorrelation plot, we use the acf() function; the ggplot version uses autoplot()

Autocorrelation plots

library(ggfortify)
auto_corr <- acf(co2_tbl$co2_val, plot = FALSE)
autoplot(auto_corr)

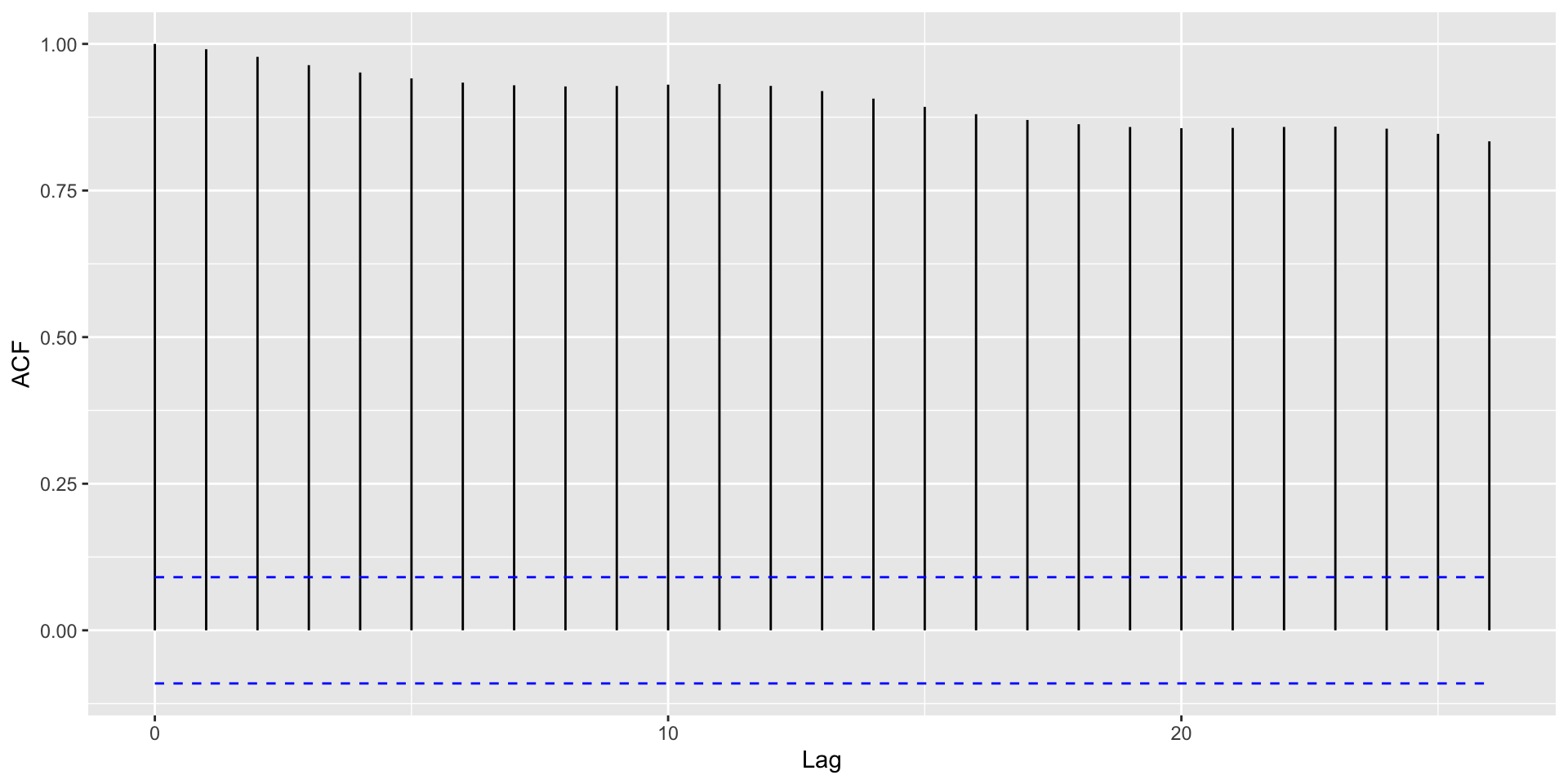
Autocorrelation Plots and Seasonality

With strong global trends, autocorrelations will be very positive.

. . .

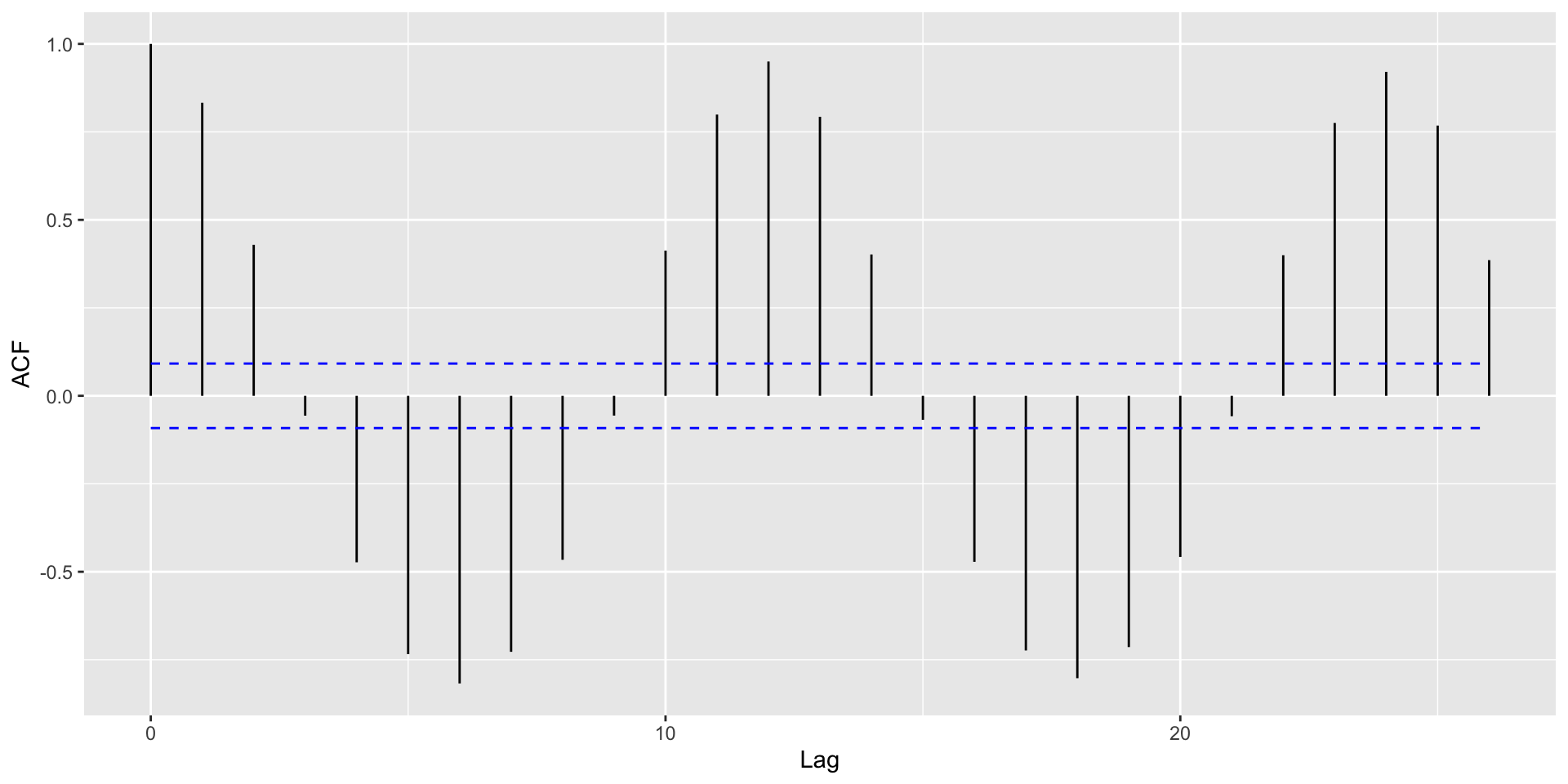
Helpful: Visualize autocorrelations after removing the global trend (compute moving average with rollapply())

Autocorrelation Plots and Seasonality

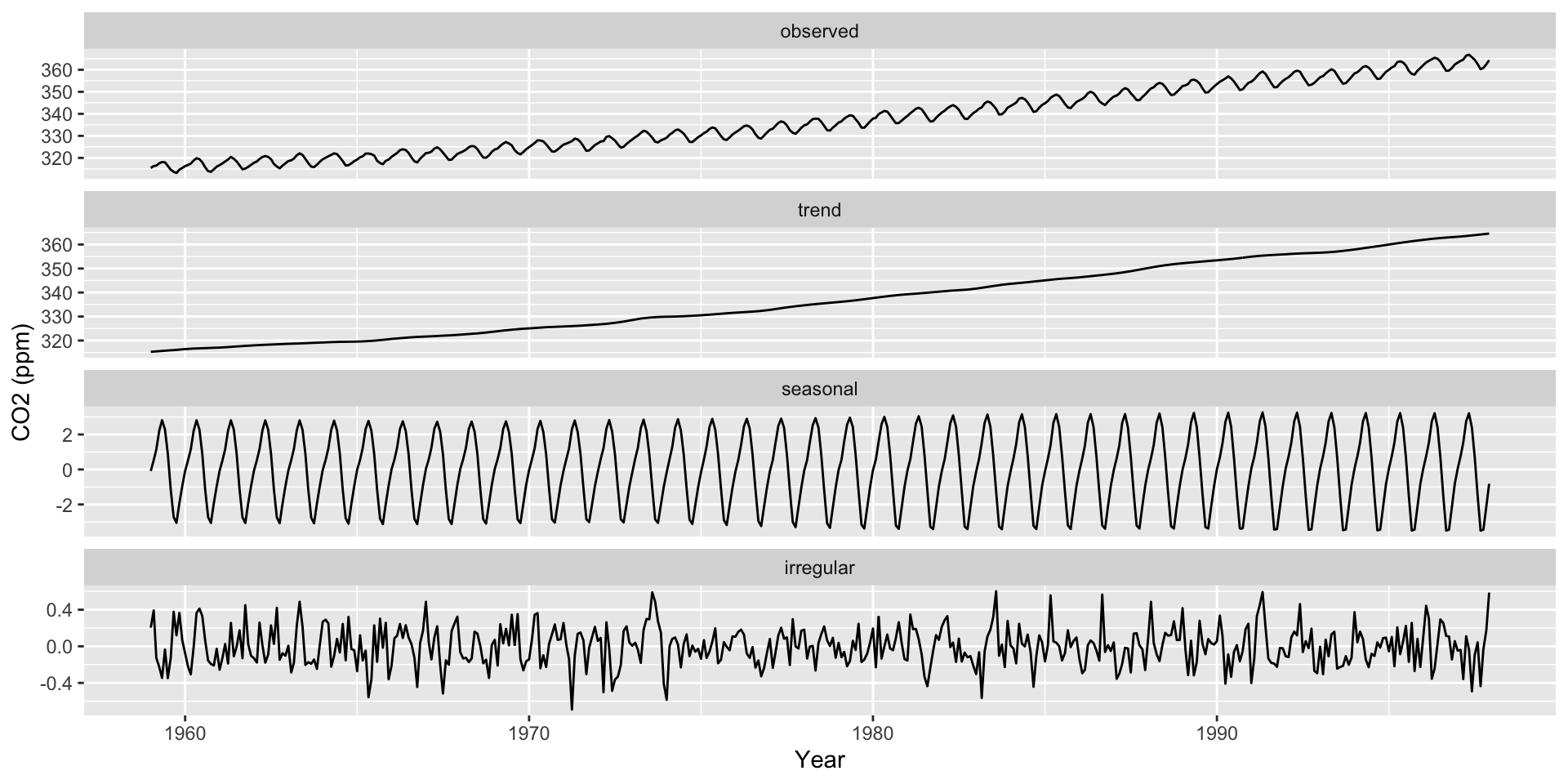
Seasonality Decomposition

Remember that there are three main components to a time series:

  1. Average trends

  2. Seasonality

  3. Noise

. . .

Use ggsdc() (from ggseas) to decompose a time series into these three components

  • Plots the observed time series.

  • Plots a loess curve as the global trend.

  • Plots another loess curve on (observed - trend) as the seasonality.

  • Plots the noise (observed - trend - seasonality).

Seasonality Decomposition

co2_tbl |>
  ggsdc(aes(obs_date, co2_val), frequency = 12, method = "stl", s.window = 12) +
  geom_line() + labs(x = "Year", y = "CO2 (ppm)")

How should we think about spatial data?

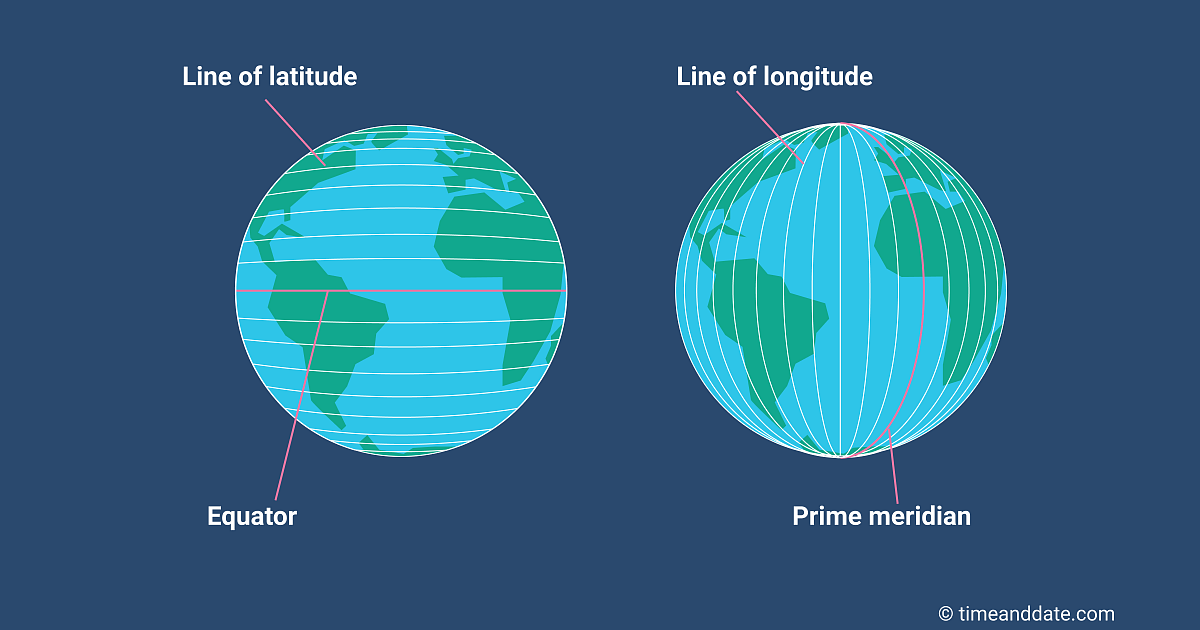
Typically location is measured with latitude / longitude (2D)

  • Latitude: Measures North / South (the “y-axis”)

    • Range is \((-90^{\circ}, 90^{\circ})\)

    • Measures degrees from the equator \((0^{\circ})\)

    • \((-90^{\circ}, 0^{\circ})\) = southern hemisphere

    • \((0^{\circ}, 90^{\circ})\) = northern hemisphere

  • Longitude: Measures East/West (the “x-axis”)

    • Range is \((-180^{\circ}, 180^{\circ})\)

    • Measures degrees from the prime meridian \((0^{\circ})\) in Greenwich, England

    • \((-180^{\circ}, 0^{\circ})\) = eastern hemisphere

    • \((0^{\circ}, 180^{\circ})\) = western hemisphere

Latitude and Longitude

Map Projections

Map projections: Transformation of the lat / long coordinates on a sphere (the earth) to a 2D plane

Mercator Projection (1500s)

Mercator Projection (Tissot indicatrix)

Robinson Projection (Standard from 1963-1998)

Robinson Projection (Tissot indicatrix)

Winkel Tripel Projection (proposed 1921, now the standard)

Winkel Tripel Projection (Tissot indicatrix)

And many more… (see xkcd comic)

Visualizing spatial data on maps using ggmap

library(ggmap)
# First, we'll draw a "box" around the US (in terms of latitude and longitude)
US <- c(left = -125, bottom = 10, right = -67, top = 49)
map <- get_stadiamap(US, zoom = 5, maptype = "stamen_toner_lite")

# Visualize the basic map
ggmap(map)

  • Draw map based on lat / lon coordinates

  • Put the box into get_stadiamap() to access Stamen Maps (you need an API key!)

  • Draw the map using ggmap() to serve as base

Visualizing spatial data on maps using ggmap

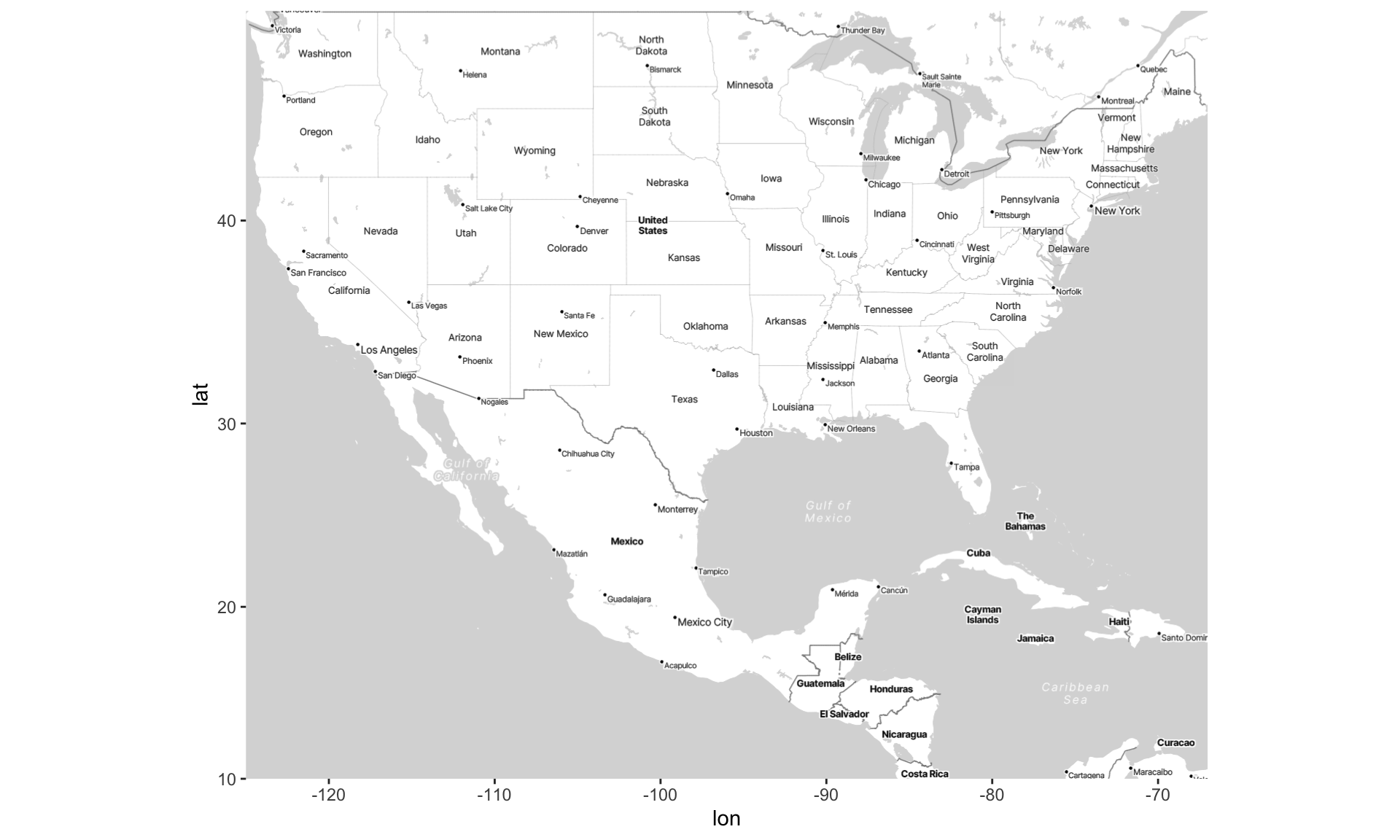
Three main types of spatial data

  1. Point Pattern Data: lat-long coordinates where events have occurred

  2. Point-Referenced data: Latitude-longitude (lat-long) coordinates as well as one or more variables specific to those coordinates.

  3. Areal Data: Geographic regions with one or more variables associated with those regions.

  • Each type is structured differently within a dataset

  • Each type requires a different kind of graph(s)

We’re going to review each type of data. Then, we’re going to demonstrate how to plot these different data types

  • Today: Point-referenced and point pattern

  • Monday: Areal data

Point-Pattern data

  • Point Pattern Data: lat-long coordinates where events have occurred

  • Point pattern data simply records the lat-long of events; thus, there are only two columns

  • Again, latitude and longitude are represented with dots, sometimes called a dot or bubble map.

  • The goal is to understand how the density of events varies across space

  • The density of the dots can also be visualized (e.g., with contours)

    • Use methods we’ve discussed before for visualizing 2D joint distribution

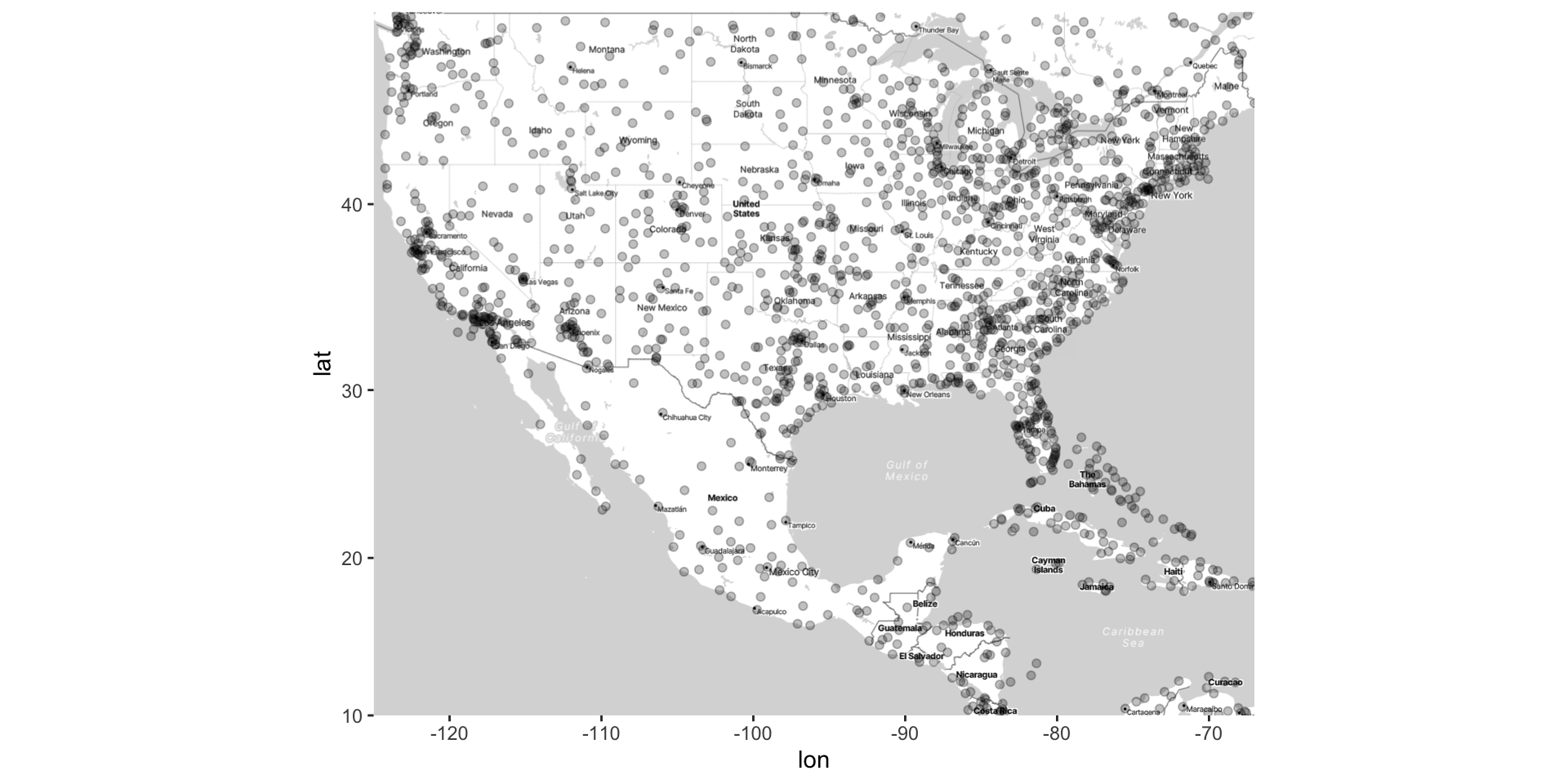
Point-Referenced data

  • Point-Referenced data: Latitude-longitude (lat-long) coordinates as well as one or more variables specific to those coordinates

  • Point-referenced data will have the following form:

airports |> dplyr::select(lat, lon, altitude, n_depart, n_arrive, name) |> slice(1:3)
# A tibble: 3 × 6
    lat   lon altitude n_depart n_arrive name                        
  <dbl> <dbl>    <dbl>    <int>    <int> <chr>                       
1 -6.08  145.     5282        5        5 Goroka Airport              
2 -5.21  146.       20        8        8 Madang Airport              
3 -5.83  144.     5388       10       12 Mount Hagen Kagamuga Airport

  • The goal is to understand how the variable(s) (e.g., altitude) vary across different spatial locations

  • Typically, the latitude and longitude are represented with dots, and the variable(s) are represented with size and/or colors

Adding points to the map as usual

ggmap(map) +
  geom_point(data = airports, aes(x = lon, y = lat), alpha = 0.25)

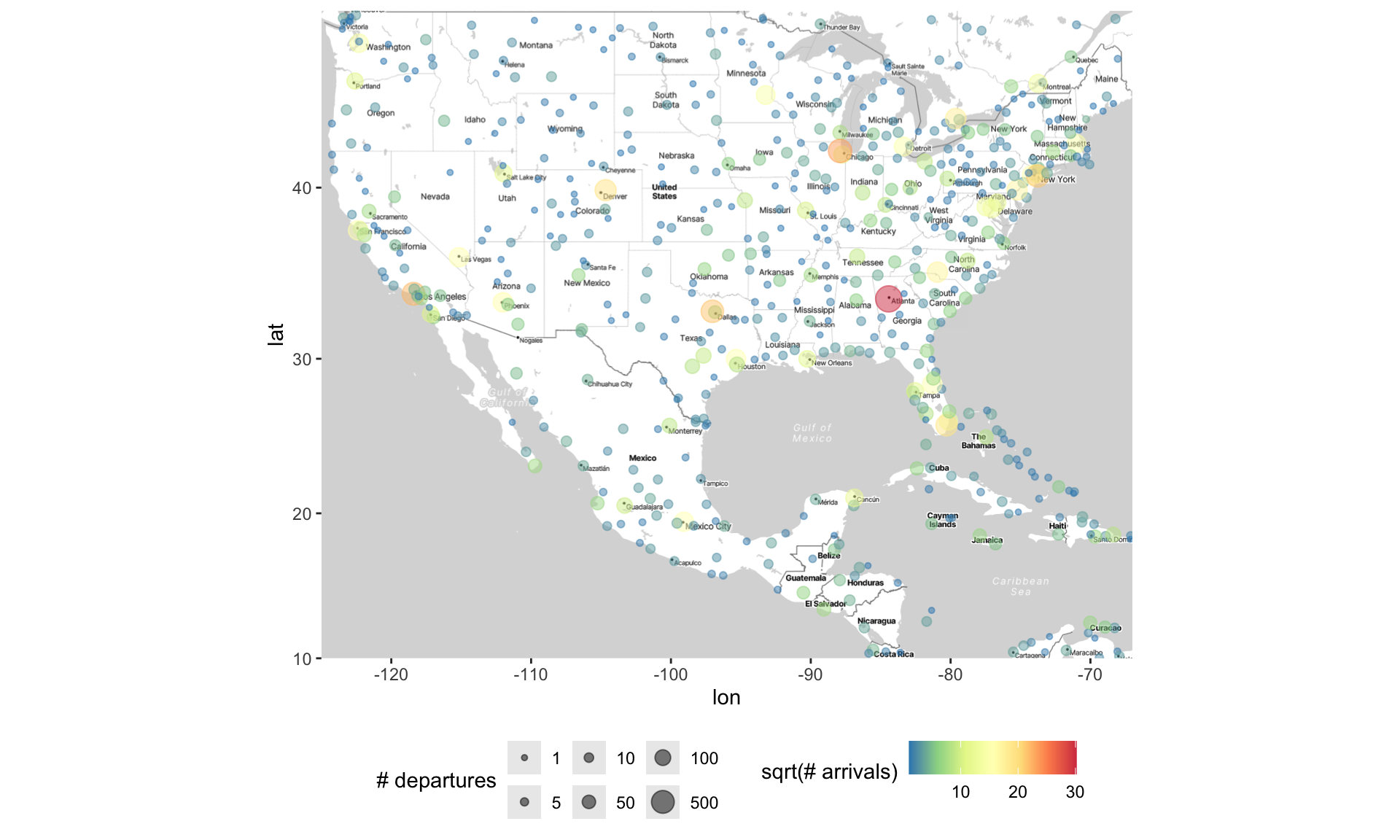
Altering points on the map (in the usual way)

ggmap(map) +
  geom_point(data = airports, 
             aes(x = lon, y = lat, 
                 size = sqrt(n_depart), color = sqrt(n_arrive)),
             alpha = .5) +
  scale_size_area(breaks = sqrt(c(1, 5, 10, 50, 100, 500)), 
                  labels = c(1, 5, 10, 50, 100, 500), 
                  name = "# departures") +
  scale_color_distiller(palette = "Spectral") +
  labs(color = "sqrt(# arrivals)") +
  theme(legend.position = "bottom")

Altering points on the map (in the usual way)

Inference for Spatial Data

There are whole courses, textbooks, and careers dedicated to this. We’re not going to cover everything!

However, there are some straightforward analyses that can be done for spatial data.

Point-Referenced Data:

  • Divide geography into groups (e.g., north/south/east/west) and use regression to test if there are significant differences.

  • Regression of \(\text{outcome} \sim \text{latitude} + \text{longitude}\). Smoothing regression (e.g., loess) is particularly useful here.

Visualizing Inference for Point-Reference Data

For basic linear regression:

  1. Plot \((x, y)\) as points

  2. Fit the regression model \(y \sim x\), to give us \(\hat{y} = \hat{\beta}_0 + \hat{\beta}_1 \cdot x\)

  3. Plot \((x, \hat{y})\) as a line

For point reference data, we have the following variables:

  • Inputs are longitude \(x\) and latitude \(y\), and outcome variable is \(z\)

Consider the following linear regression model: \(z \sim \text{lat} + \text{long}\)

Goal: Make a visual involving \((\text{long}, \text{lat}, \hat{z})\), and possibly \(z\).

Kriging

Goal: Make a visual involving (long, lat, \(\hat{z}\)) and possibly \(z\)

Want \(\hat{z}\) for many (long, lat) combos (not just the observed one!)

To do this, follow this procedure:

  1. Fit the model \(z \sim \text{lat} + \text{long}\)

  2. Create a grid of \((\text{long}, \text{lat})_{ij}\)

  3. Generate \(\hat{z}_{ij}\) for each \((\text{long}, \text{lat})_{ij}\)

  4. Plot a heat map or contour plot of (long, lat, \(\hat{z}\))

  • You can also add the actual \(z\) values (e.g., via size) on the heat map

This is known as kriging, or spatial interpolation

Kriging: airline data example

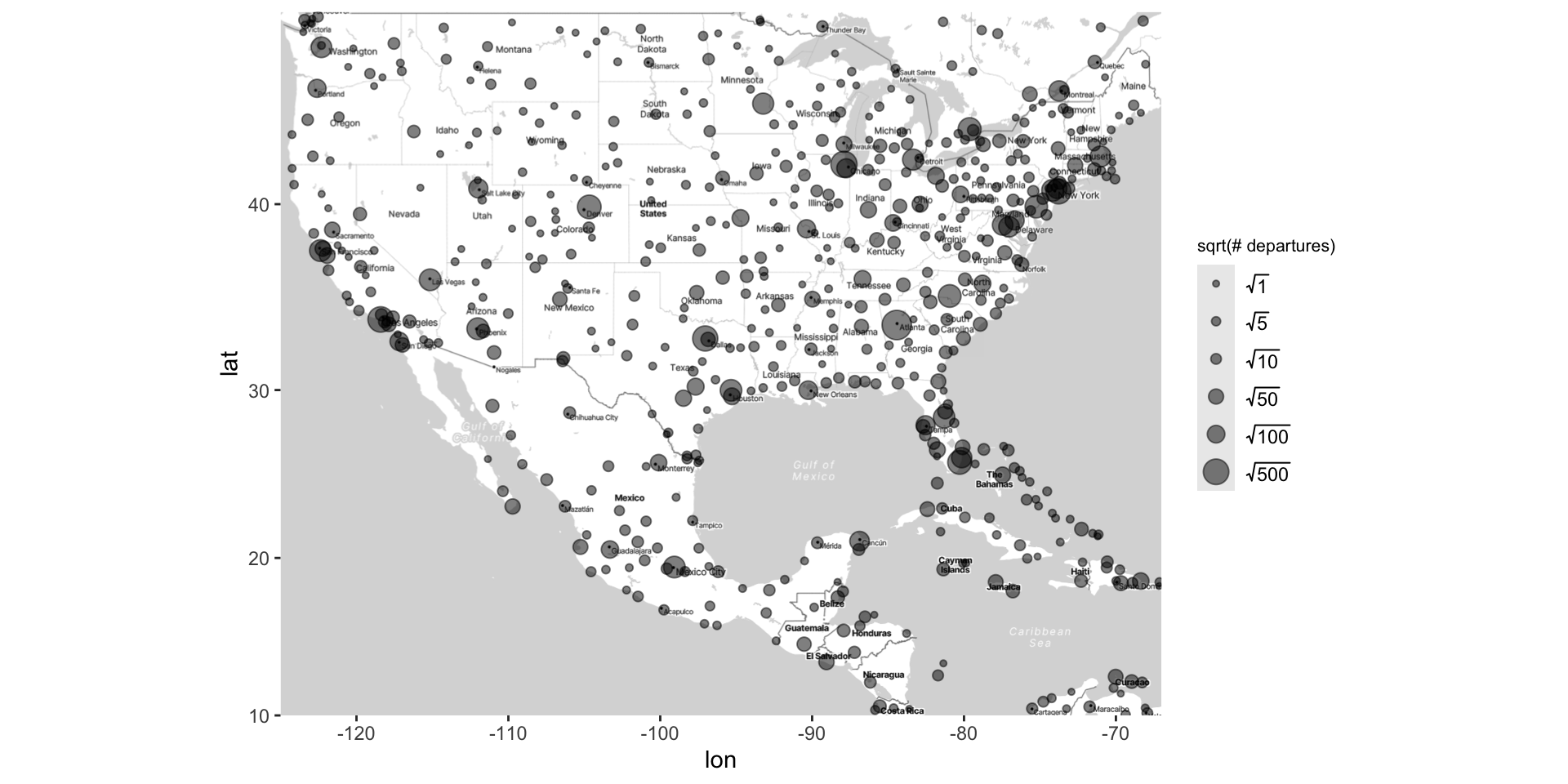
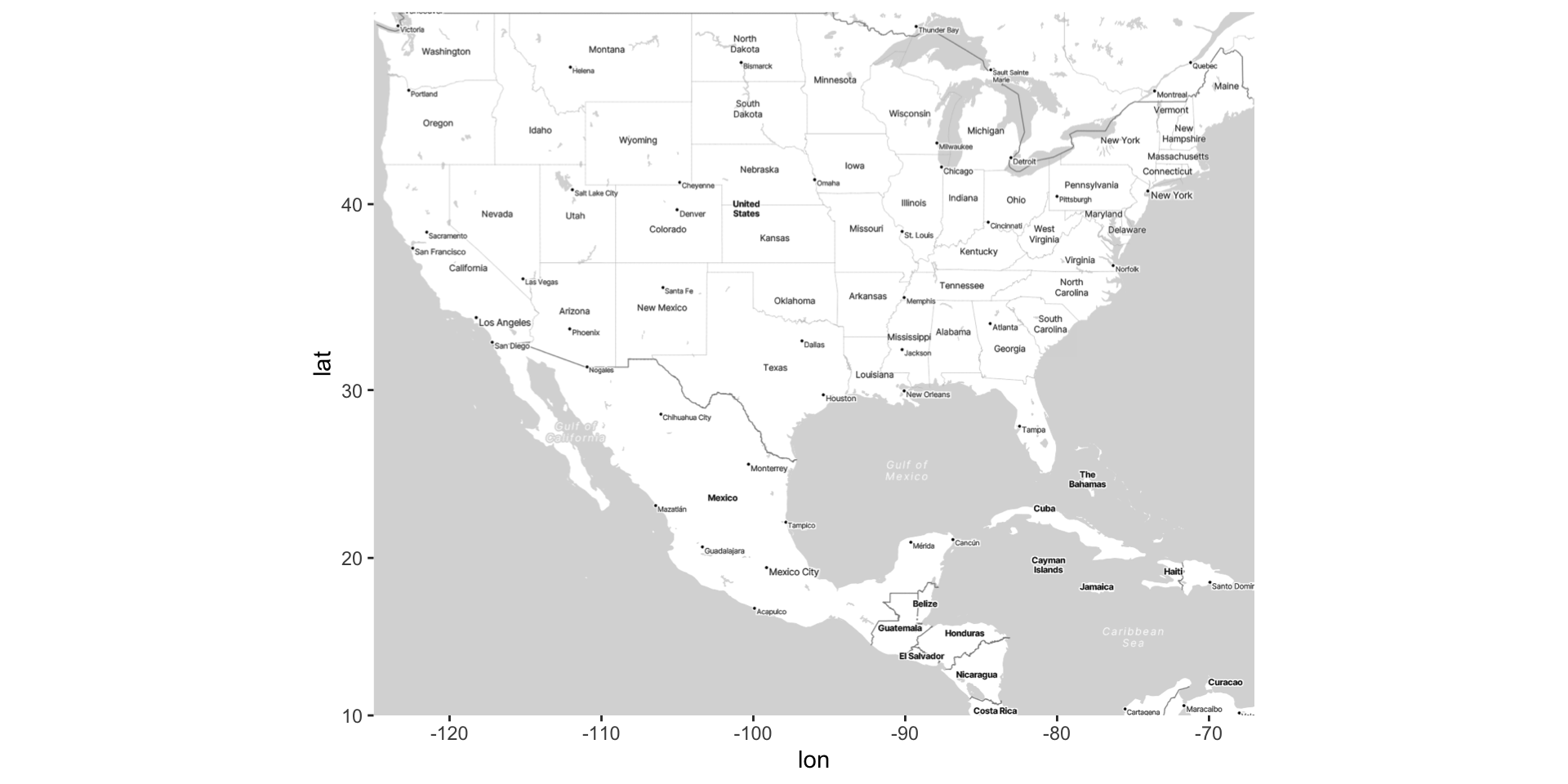
Kriging: creating the map

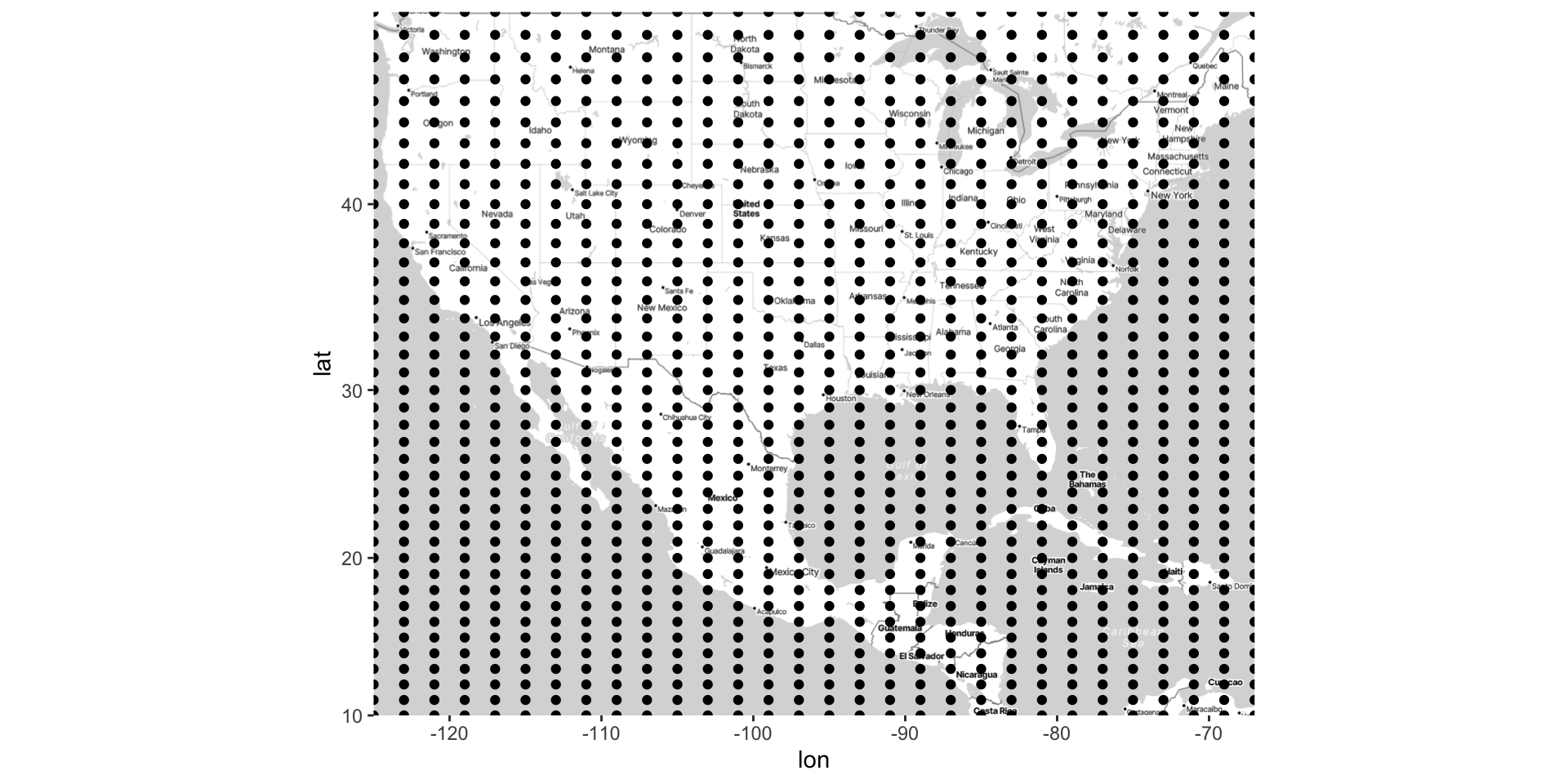
Kriging: generating the grid

Kriging: generating predicted values

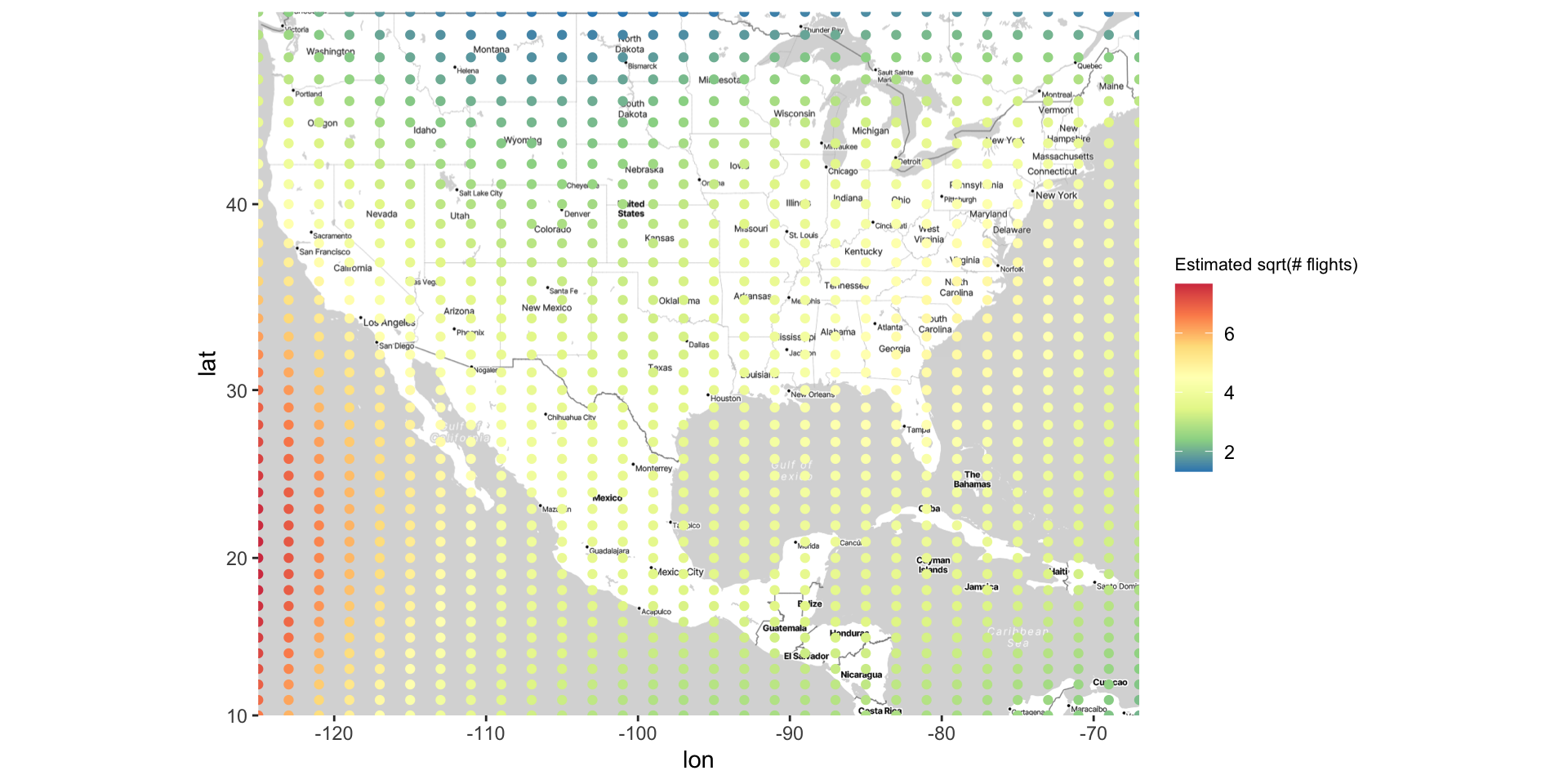
Kriging: plotting heat map of predicted values

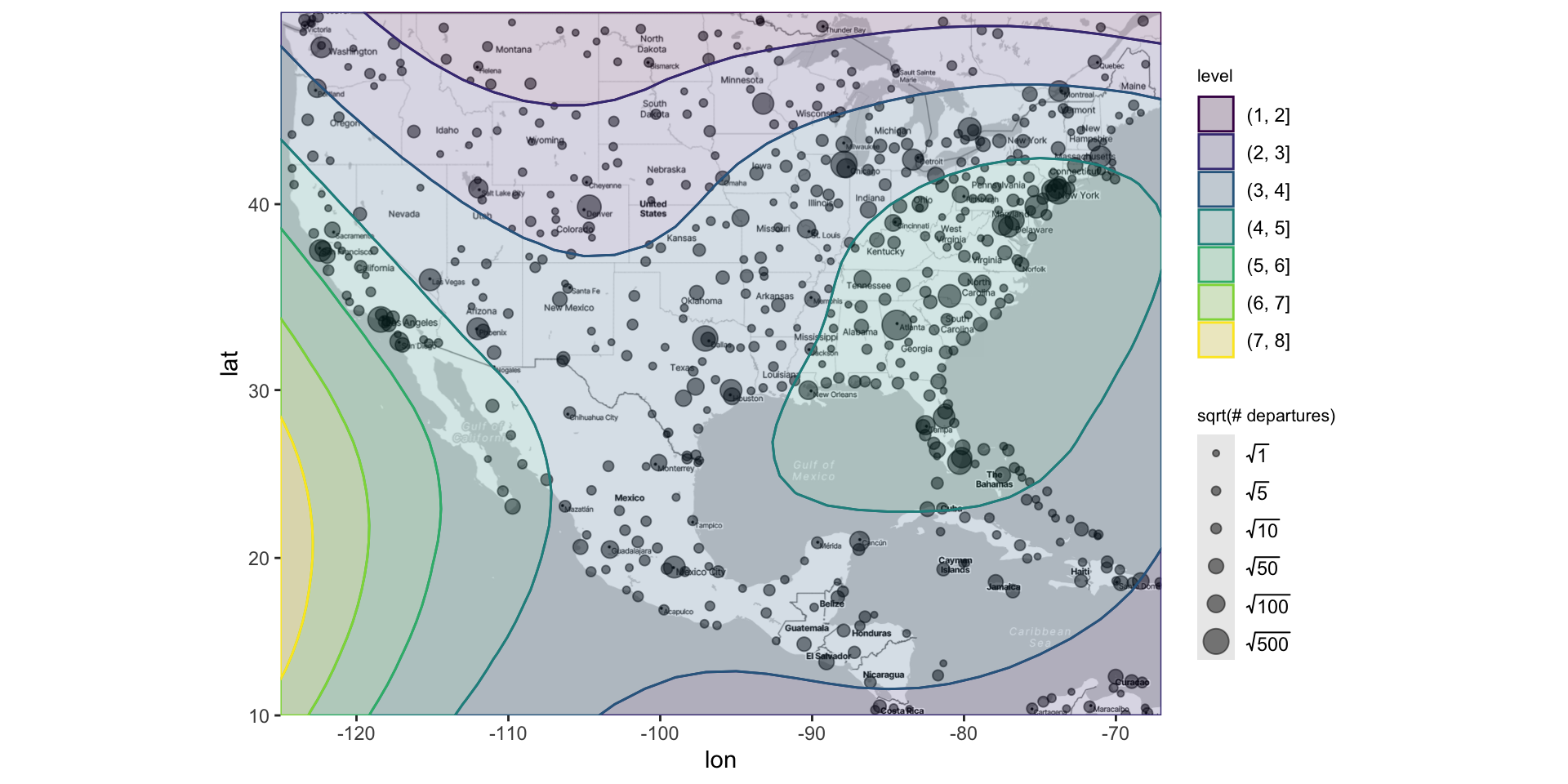
Kriging overview

The steps used to create this map are…

  1. Fit an interactive regression model using loess()

  2. Make a grid of lat/long coordinates, using seq() and expand.grid()

  3. Get estimated outcomes across the grid using predict()

  4. Use geom_contour_filled() to color map by estimated outcomes

Recap and next steps

  • Walked through basics of time series data, such as moving averages, autocorrelation, seasonality

  • Visualized spatial data in a 2D plane (latitude/longitude), i.e., maps

    • Point pattern: Scatterplots with density contours

    • Point-referenced: Scatterplots with color/size, use regression/loess for inference