# Need to have the tidyverse installed prior to starting!
library(tidyverse)
nfl_games <- read_csv("https://data.scorenetwork.org/data/nfl_mahomes_era_games.csv") |>
filter(season == 2023)Introduction to Elo ratings (INSTRUCTOR SOLUTIONS)
An introduction to Elo ratings using NFL game outcomes.
Intro and Data
The purpose of this module is to introduce the basics of Elo ratings in the context of measuring NFL team strengths. This file contains guided exercises demonstrating how to implement Elo ratings from scratch in R.
We’ll use a subset of the NFL Game Outcomes dataset available on the SCORE Sports Data Repository, only considering games during the 2023-24 season. The following code chunk reads in the larger dataset and filters down to only include games during the 2023-24 season:
As indicated in the overview page for the larger dataset, each row in the dataset corresponds to a single game played during the 2023-24 season:
nfl_games# A tibble: 285 × 10
season game_id game_type week home_team away_team home_score away_score
<dbl> <chr> <chr> <dbl> <chr> <chr> <dbl> <dbl>
1 2023 2023_01_DET… REG 1 KC DET 20 21
2 2023 2023_01_CAR… REG 1 ATL CAR 24 10
3 2023 2023_01_HOU… REG 1 BAL HOU 25 9
4 2023 2023_01_CIN… REG 1 CLE CIN 24 3
5 2023 2023_01_JAX… REG 1 IND JAX 21 31
6 2023 2023_01_TB_… REG 1 MIN TB 17 20
7 2023 2023_01_TEN… REG 1 NO TEN 16 15
8 2023 2023_01_SF_… REG 1 PIT SF 7 30
9 2023 2023_01_ARI… REG 1 WAS ARI 20 16
10 2023 2023_01_GB_… REG 1 CHI GB 20 38
# ℹ 275 more rows
# ℹ 2 more variables: game_outcome <dbl>, score_diff <dbl>Note the game_type column indicates if the game was during the regular season (REG), or during the playoffs with the different values indicating the different playoff rounds:
table(nfl_games$game_type)
CON DIV REG SB WC
2 4 272 1 6 The week column just increases in the correct order, which will be convenient for implementing Elo ratings over the course of the NFL season.
Background Information
Elo ratings were created by physicist Arpad Elo in the 1960s for rating chess players. The main idea behind Elo ratings is to create an exchange in rating points between players (or teams) after a match. The simplest version of this system was constructed to be a zero-sum rating, such that the winner gains x points while the same number of x points are subtracted from the loser’s rating. If the win was expected, the winner receives fewer points than if the win was unexpected (i.e., an upset) - where the expectation is set prior to the match. This system results in a dynamic rating that is adjusted for opponent quality.
Method Details
We’re going to consider a simple version of Elo ratings in the context of measuring NFL team strength via a rating. Let the rating for the home team be \(R_{\text{home}}\) and the away team rating be \(R_{\text{away}}\). Then the expected score for the home team \(E_{\text{home}}\) is calculated as:
\[ E_{\text{home}} = \frac{1}{1+10^{\left(R_{\text{away}}-R_{\text{home}}\right) / 400}}, \]
and the expected score for the away team \(E_{\text{away}}\) is computed in a similar manner:
\[ E_{\text{away}} = \frac{1}{1+10^{\left(R_{\text{home}}-R_{\text{away}}\right) / 400}}. \] These expected scores represent the probability of winning1, e.g., \(E_{\text{home}}\) represents the probability of winning for the home team.
The choice of 10 and 400 in the denominator may appear arbitrary at first, but they correspond to:
- a logistic curve (thus bounded by 0 and 1) with base 10, and
- a scaling factor of 400 which can be tuned to yield better predictions (discussed in more detail below).
A more general representation of the expected score would replace the choice of 10 with some constant (e.g., \(e\)) and replace 400 with a tune-able quantity \(d\). For now though we will just use 10 and 400 since they are the original choices.
While the above quantities represent the expectation of a game between teams with ratings \(R_{\text{home}}\) and \(R_{\text{away}}\), we need a step to update the ratings after observing the game outcome. We can update we update the ratings for the home team based on the observed score \(S_{\text{home}}\):
\[ R^{\text{new}}_{\text{home}} = R_{\text{home}} + K \cdot (S_{\text{home}} - E_{\text{home}}) \]
The observed score \(S_{\text{home}}\) is based on the game outcome such that,
- \(S_{\text{home}} = 1\) if the home team wins,
- \(S_{\text{home}} = 0.5\) if it is a draw, or
- \(S_{\text{home}} = 0\) if the home team loses.
We compute the updated rating for the away team \(R^{\text{new}}_{\text{away}}\) in a similar manner, by replacing home team quantities with those with respect to the away team.
The quantity \(K\) is known as the update factor, indicating the maximum number of Elo rating points a team gains from winning a single game (and how many points are subtracted if they lose). This is a tuning parameter, which ideally should be selected to yield optimal predictive performance.
Although the details are beyond the scope of this module, there is a relationship between this Elo ratings update formula with stochastic gradient descent for logistic regression.
Learn by Doing
We’ll now proceed to implement Elo ratings for NFL teams during the 2023-24 season in R.
Calculating and Updating Ratings
We will start by creating two helper functions to compute the expected scores and updated ratings after a game.
NFL Elo Ratings
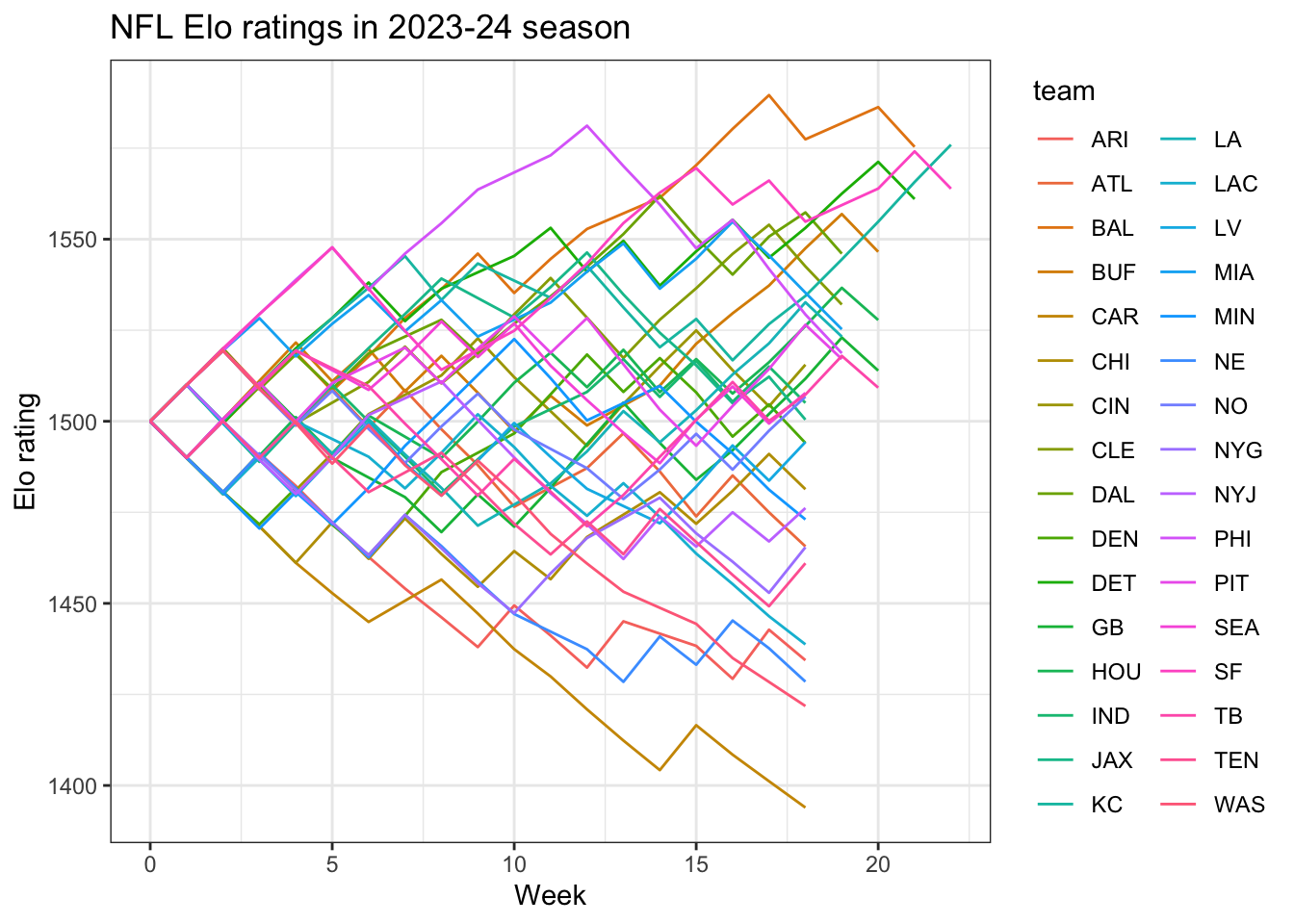
Now with the basics, let’s move on to perform these calculations over the entire season, updating a table to include each team’s Elo rating following every game. We can implement this using a for loop to proceed through each game in the nfl_games table, looking up each team’s previous ratings and performing the above calculations.
Prior to beginning this loop, we will set-up a table initializing each team with a rating of 1500. This a naive approach since we likely have prior knowledge about each team’s strength before the start of the season, but we’ll discuss this in more detail at the end of the module. For now, we’ll use 1500 since it is a common choice for initializing Elo ratings. The code chunk below initializes this starting table of ratings beginning with an imaginary week 0:
nfl_elo_ratings <- tibble(team = unique(nfl_games$home_team),
elo_rating = 1500,
week = 0)
nfl_elo_ratings# A tibble: 32 × 3
team elo_rating week
<chr> <dbl> <dbl>
1 KC 1500 0
2 ATL 1500 0
3 BAL 1500 0
4 CLE 1500 0
5 IND 1500 0
6 MIN 1500 0
7 NO 1500 0
8 PIT 1500 0
9 WAS 1500 0
10 CHI 1500 0
# ℹ 22 more rowsAfter you run the completed for loop, you can view and inspect the ratings in different ways. For example, the following code chunk will return the final rating for each after the completion of the entire season of games:
nfl_elo_ratings |>
group_by(team) |>
# Since some teams make the playoffs, need to find the rating
# for each team's final weeK:
summarize(final_rating = elo_rating[which.max(week)]) |>
# Sort in descending order of the rating so the best team is first:
arrange(desc(final_rating))# A tibble: 32 × 2
team final_rating
<chr> <dbl>
1 KC 1576.
2 BAL 1575.
3 SF 1564.
4 DET 1561.
5 BUF 1547.
6 DAL 1546.
7 CLE 1532.
8 HOU 1528.
9 MIA 1525.
10 LA 1523.
# ℹ 22 more rows
BONUS: Expand To Visualize Ratings
It is often helpful to visualize how the team ratings are changing over time. While this module does not cover the details about the ggplot2 visualization library, the following code creates a line for each team:
nfl_elo_ratings |>
# Input the dataset into ggplot, mapping the week to the x-axis and
# the elo_rating to the y-axis, colored by team:
ggplot(aes(x = week, y = elo_rating, color = team)) +
geom_line() +
theme_bw() +
labs(x = "Week", y = "Elo rating",
title = "NFL Elo ratings in 2023-24 season")
While we can observe ratings changing over the season for every team, this visualization is less than ideal. Instead one could take advantage of the team colors available using the load_teams function from the nflverse This is a little more involved, but here is example way to create a figure highlighting teams in each division separately (this requires installing the nflreadr, ggrepel, and cowplot packages:
library(nflreadr)
nfl_team_colors <- load_teams() |>
dplyr::select(team_abbr, team_division, team_color)
# Create a dataset that has each team's final Elo rating
nfl_team_final <- nfl_elo_ratings |>
group_by(team) |>
summarize(week = max(week),
elo_rating = elo_rating[which.max(week)],
.groups = "drop") |>
inner_join(nfl_team_colors, by = c("team" = "team_abbr")) |>
arrange(desc(elo_rating))
# Need ggrepel:
library(ggrepel)
division_plots <-
lapply(sort(unique(nfl_team_final$team_division)),
function(nfl_division) {
# Pull out the teams in the division
division_teams <- nfl_team_final |>
filter(team_division == nfl_division) |>
mutate(team = fct_reorder(team, desc(elo_rating)))
# Get the Elo ratings data just for these teams:
division_data <- nfl_elo_ratings |>
filter(team %in% division_teams$team) |>
mutate(team = factor(team,
levels = levels(division_teams$team))) |>
# Make text labels for them:
group_by(team) |>
mutate(team_label = if_else(week == max(week),
as.character(team),
NA_character_)) |>
ungroup()
# Now make the full plot
nfl_elo_ratings |>
# Plot all of the other teams as gray lines:
filter(!(team %in% division_teams$team)) |>
ggplot(aes(x = week, y = elo_rating, group = team)) +
geom_line(color = "gray", alpha = 0.5) +
# But display the division teams with their colors:
geom_line(data = division_data,
aes(x = week, y = elo_rating, group = team,
color = team)) +
geom_label_repel(data = division_data,
aes(label = team_label,
color = team), nudge_x = 1, na.rm = TRUE,
direction = "y") +
scale_color_manual(values = division_teams$team_color,
guide = FALSE) +
theme_bw() +
labs(x = "Week", y = "Elo rating",
title = paste0("Division: ", nfl_division))
})
# Display the grid of plots with cowplot!
library(cowplot)
plot_grid(plotlist = division_plots, ncol = 2, align = "hv")
Assessing the Ratings
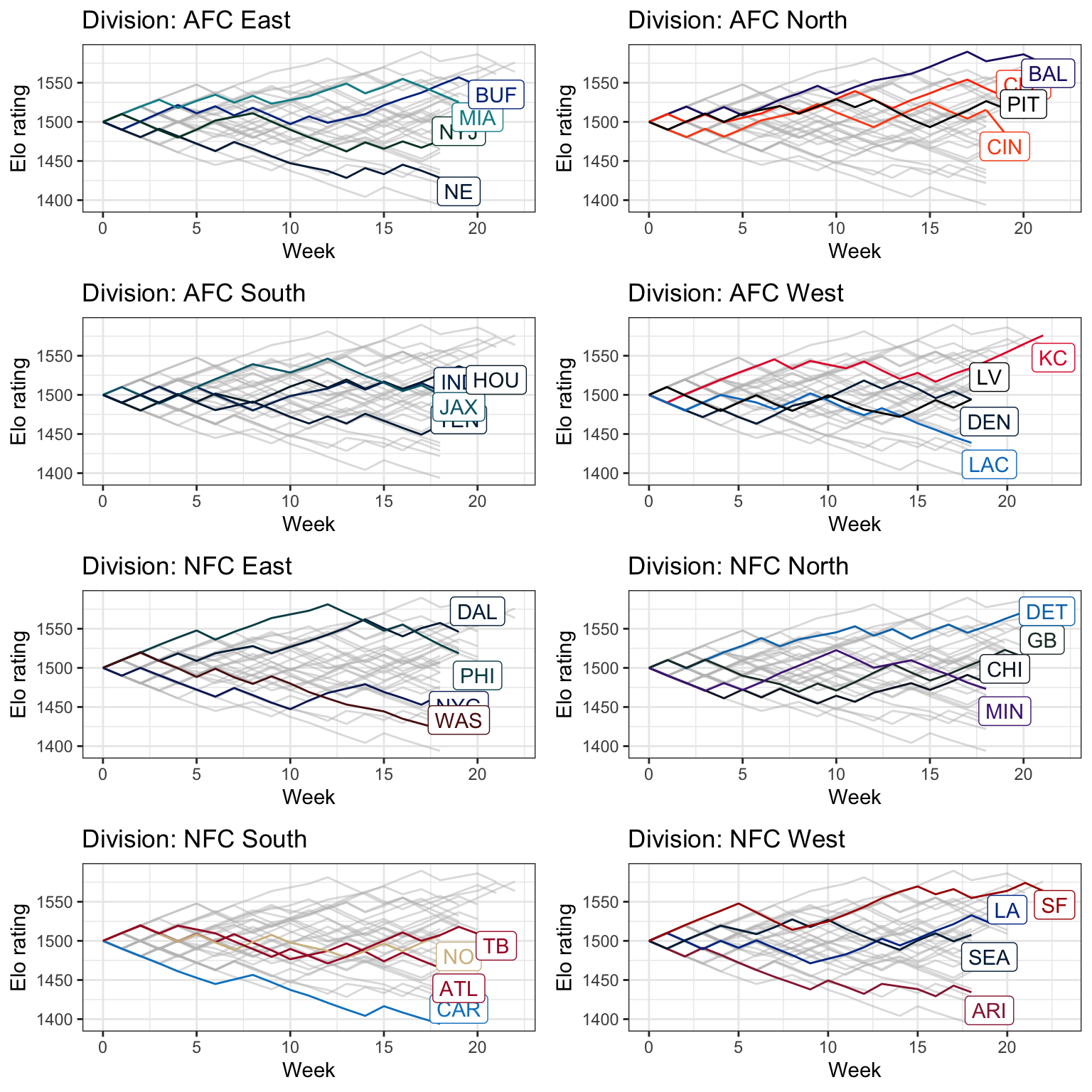
The result of the for loop from above provides us with a dataset that contains the rating for each team after every week. But how do we know if we can trust this approach for estimating team ratings? We can assess the predictive performance of the Elo ratings based on the estimated probabilities for every game given the team’s ratings entering the game.
We will now make two copies of the complete_nfl_elo_ratings table - one to use for home teams and another to use for away teams. The code chunk below initializes these copies, and also adds 1 to the week column to indicate which week to use team’s rating for when predicting:
home_elo_ratings <- complete_nfl_elo_ratings |>
mutate(week = week + 1) |>
# Rename the team and elo_rating columns
rename(home_team = team,
home_elo_rating = elo_rating)
# And repeat for away teams:
away_elo_ratings <- complete_nfl_elo_ratings |>
mutate(week = week + 1) |>
rename(away_team = team,
away_elo_rating = elo_rating)Next, we can join the ratings stored in these two tables to the nfl_games table to estimate the expected outcome with respect to the home team. The following code chunk demonstrates how to left_join the team ratings, and then compute the probability of winning for the home team:
upd_nfl_games <- nfl_games |>
# First join home team by the team abbreviation and week
left_join(home_elo_ratings, by = c("home_team", "week")) |>
# Repeat for away team ratings:
left_join(away_elo_ratings, by = c("away_team", "week")) |>
# And now compute the expectation, home_win_prob:
mutate(home_win_prob = calc_expected_score(home_elo_rating,
away_elo_rating))
upd_nfl_games# A tibble: 285 × 13
season game_id game_type week home_team away_team home_score away_score
<dbl> <chr> <chr> <dbl> <chr> <chr> <dbl> <dbl>
1 2023 2023_01_DET… REG 1 KC DET 20 21
2 2023 2023_01_CAR… REG 1 ATL CAR 24 10
3 2023 2023_01_HOU… REG 1 BAL HOU 25 9
4 2023 2023_01_CIN… REG 1 CLE CIN 24 3
5 2023 2023_01_JAX… REG 1 IND JAX 21 31
6 2023 2023_01_TB_… REG 1 MIN TB 17 20
7 2023 2023_01_TEN… REG 1 NO TEN 16 15
8 2023 2023_01_SF_… REG 1 PIT SF 7 30
9 2023 2023_01_ARI… REG 1 WAS ARI 20 16
10 2023 2023_01_GB_… REG 1 CHI GB 20 38
# ℹ 275 more rows
# ℹ 5 more variables: game_outcome <dbl>, score_diff <dbl>,
# home_elo_rating <dbl>, away_elo_rating <dbl>, home_win_prob <dbl>We can now assess the use of the Elo rating system with the computed home_win_prob values relative to the observed game_outcome. While there are a number of ways to evaluate the performance of a probability estimate, in this module we will consider the use of the Brier score which is computed as the mean squared difference between the observed outcome and predicted probabilities. In the context of our Elo rating system notation, the Brier score is computed across \(N\) games as:
\[ \frac{1}{N} \sum_{i = 1}^{N} (S_{\text{home},i} - E_{\text{home},i})^2 \] where the use of subscript \(i\) refers to the outcome and expectation for the home team in game \(i\).
We will compute the Brier score using our NFL Elo ratings, and compare the performance to always using a 50/50 probability for every game, i.e., as if we never learned any information over the course of the season.
Although you have just implemented and evaluated the use of Elo ratings in the context of NFL games, so far we have just considered an update factor of \(K = 20\). But is there a more optimal choice?
Discussion
You have now learned the basics behind the popular Elo rating system in sports, including the steps for implementing Elo ratings from scratch in R to measure NFL team strength. Furthermore, you have a basic understanding for how to assess the predictive performance of the ratings using Brier score and how this can be used to tune the choice the update factor \(K\). Although we only considered the ratings for the 2023-24 season, you could observe how ratings change across a larger dataset of games spanning the Patrick Mahomes’ era.
However, there are a number of additional questions and considerations that we did not cover in this module such as:
Initial Elo ratings: Rather than using 1500 as the initial values for every team, you could use a more informed starting point such as Neil Paine’s NFL Elo ratings which start at the beginning of the league history.
New season? New roster?: We just demonstrated Elo ratings within one season, but what do we do across multiple seasons? Do we simply just use the final rating from the previous season as the initial rating in the following season? But teams change rosters so we likely want to make some correction.
Scaling factor: We fixed the scaling factor to be 400 in this module, but we could also tune this quantity in the same manner as \(K\).
What games matter in assessment?: Although we walked through assessing the performance Elo ratings performance with Brier scores, we treated every game equally in this calculation. What if we wanted to tune our Elo rating system to yield the most optimal predictions in the playoffs, and ignore performance in the first few weeks of the season?
What about margin of victory?: We only considered win/loss in a binary manner, but the score differential in a game may be informative of team strength. There are extensions to handle margin of victory in Elo ratings, but details are beyond the scope of this module.
With these considerations in mind, you now have the capability in implement Elo ratings in practice across a variety of sports.
You may find these additional resources helpful:
For football fans, you can simulate NFL seasons using your Elo ratings with the
nflseedRpackage.The
elopackage inRprovides convenient functions for computing Elo ratings, similar to the functions we defined above.An overview of the popular Glicko rating system by statistician Mark Glickman that quantifies uncertainty about the ratings.
Footnotes
Technically, it represents the probability of winning and half the probability of drawing, but for our purposes we will just treat this as the probability of winning due to how rare draws are in the NFL.↩︎